Поднятие степени из знаменателя в числитель и наоборот
Если знаменатель дробного выражения содержит степень, то данную степень можно поднять в числитель, изменив знак показателя этой степени на противоположный. Значение выражения при этом не меняется. Данное преобразование иногда используется при упрощении выражений.
Рассмотрим следующее равенство:
Данное равенство является верным, поскольку выражение равно 2, а любое число в нулевой степени есть единица.
Попробуем поднять степень 22 из знаменателя в числитель, изменив знак показателя этой степени на противоположный. При этом, поднятую степень и ту степень, которая располагалась в числителе, соединим знаком умножения:
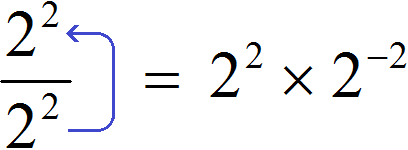
Получили выражение 22 × 2−2. Чтобы его вычислить, воспользуемся основным свойством степени:
22 × 2−2 = 22 + (−2) = 2 = 1
Получился тот же результат, что и раньше. Значит значение выражения не изменилось. Как это работает?
Если в равенстве поменять местами левую и правую часть, то получим равенство . Это позволяет заменять в выражениях дробь вида на тождественно равное ей выражение a−n.
Теперь представим выражение в виде произведения . То есть . Напомним, что при замене деления умножением, делимое умножают на число, обратное делителю. А обратное делителю число в данном случае это дробь
Теперь воспользуемся правилом . В произведении заменим дробь на тождественно равное ей выражение 2−2
Далее, как и раньше применяем основное свойство степени:
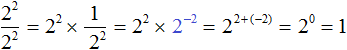
Получился тот же результат 1.
Таким же образом можно опустить степень из числителя в знаменатель, изменив знак показателя этой степени на противоположный.
Рассмотрим выражение . Чтобы найти его значение, воспользуемся правилом деления степеней с одинаковыми основаниями. В результате получим
Теперь попробуем решить этот пример, опустив степень 2−2 из числителя в знаменатель, изменив знак показателя этой степени на противоположный. При этом, опущенную степень 2−2 и ту степень, которая располагалась в знаменателе, соединим знаком умножения. А в числителе останется единица:
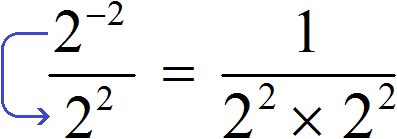
Дальнейшее вычисление не составит особого труда:
Как и в прошлом примере выражение представимо в виде произведения
Этим и объясняется появление единицы в числителе, после того как степень 2−2 была опущена в знаменатель.
Переносимых в знаменатель либо в числитель степеней может быть несколько. Например, знаменатель дроби содержит степени 32, a3, b4. Перенесём эти степени в числитель, изменив знаки их показателей на противоположные. В результате получим выражение 3−2a−3b−4.
Пример 2. Поднять степени из знаменателя дроби в числитель
Пример 3. Поднять степени из знаменателя дроби в числитель
Пример 4. Поднять степень из знаменателя дроби в числитель
Пример 5. Опустить степень из числителя дроби в знаменатель
Пример 6. Степень из числителя дроби опустить в знаменатель, а степень из знаменателя поднять в числитель
Представлять дробь в виде произведения вовсе не обязательно. Если пропустить эту запись, то данный пример можно решить короче:
Пример 7. В дроби перенести из знаменателя в числитель только те степени, которые имеют отрицательные показатели:
Пример 8. Представить произведение 3x−5 в виде дроби, не содержащей степени с отрицательным показателем.
Перепишем произведение 3x−5 с помощью знака умножения:
3 × x−5
Сомножитель 3 оставим без изменений, а сомножитель x−5 заменим на тождественно равную ему дробь
Теперь согласно правилу , умножим множитель 3 на числитель дроби . В результате образуется дробь
Пример 9. Представить произведение 3(x + y)−4 в виде дроби, не содержащей степени с отрицательным показателем.
Выражение состоит из сомножителей 3 и (x + y)−4. Сомножитель 3 оставим без изменений, а сомножитель (x + y)−4 заменим на тождественно равную ему дробь
Теперь умножим множитель 3 на числитель дроби . В результате образуется дробь
Пример 10. Представить дробь в виде произведения.
Чтобы решить этот пример, достаточно поднять степень x2 в числитель, изменив знак показателя этой степени на противоположный:
Как и в прошлых примерах дробь можно было представить в виде произведения . Затем воспользовавшись правилом , заменить сомножитель на тождественно равный ему сомножитель x−2.
Пример 11. Представить дробь в виде произведения.
Пример 12. Найти значение выражения
Поднимем степень 2−3 из знаменателя в числитель, а степень 10−2 из числителя опустим в знаменатель:
Вычислим значения степеней, содержащихся в числителе и в знаменателе:
Сократим полученную дробь на 25. Тогда останется дробь , значение которой равно 2.
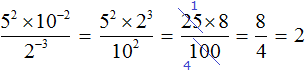
А если бы мы не подняли степень 2−3 в числитель, и степень 10−2 не опустили в знаменатель, а стали вычислять каждую степень по отдельности, то получили бы не очень компактное решение:
Запись больших и маленьких чисел
В точных науках время от времени встречаются очень большие или, наоборот, маленькие значения величин. Чтобы было комфортнее работать с ними, и тем более, одновременно использовать вместе в одних и тех же расчетах, был придуман некий общий принцип записи чисел, так называемый стандартный вид.
Чтобы в полной мере усвоить представленный ниже материал, необходимо знать, что такое степень. К примеру, продемонстрируем ее разные варианты на числе 10:
Также напомним, для того, чтобы какое-то число умножить на 10, 100, 1000, 10000 и т.д., мы просто приписываем к нему количество нулей, которое содержится в 10, 100, 1000, 10000 и т.д. Например,
То же самое касается и деления на 10, 100, 1000, 10000 и т.д., только здесь мы убираем нули:
Перечисленные выше действия можно представить в другом виде – как произведение на 10 в определенной степени:
Десятичные дроби
Если мы имеем дело с десятичным дробями, то в целом всё аналогично. При их умножении на 10, 100, 1000 и т.д. мы смещаем запятую-разделитель вправо на столько позиций, сколько нулей содержится в 10, 100, 1000 и т.д.
Если нужно разделить десятичную дробь на 10, 100, 1000 и т.д., то мы смещаем запятую влево на соответствующее нулям количество позиций:
Стандартный вид числа
В физике и других естественных науках изучаются объекты, чьи характеристики (масса, длина, скорость и т.д.) могут измеряться очень большими или очень малыми величинами. Например, масса атома железа равна 0,0000000000000000000000000927 килограмм, а масса Солнца оценивается в 1988500000000000000000000000000 килограмм. Работать с такими числами достаточно неудобно. Сложно даже сравнивать их между собой, ведь для этого надо подсчитывать количество нулей в каждом числе. Поэтому в науке часто используется особая форма чисел, которую называют стандартным видом числа. Он основан на том, что любое число можно записать как произведение числа a, находящегося в пределах от 1 до 10, и какой-нибудь целой (в том числе отрицательной) степени десятки.

Приведем примеры представления чисел в стандартном виде
90 = 9•10 = 9•101
91 = 9,1•10 = 9,1•101
900 = 9•100 = 9•102
912 = 9,12•100 = 9,12•102
Покажем случаи, когда порядок равен нулю или меньше него
7 = 7•1 = 7•10
7,63 = 7,63•1 = 7,63•10
0,8 = 8•0,1 = 8•10– 1
0,0875 = 8,75•100 = 8,75•10– 2
Посмотрите, насколько короче выглядит запись физических величин с использованием стандартного вида:
- масса Солнца: 1988500000000000000000000000000 кг = 1,9885•1030 кг;
- масса Земли: 5970000000000000000000000 кг = 5,97•1024 кг;
- масса атома железа: 0,0000000000000000000000000927 = 9,27•10-26 кг.
Пример. Укажите стандартный вид числа 76000000.
Решение. Первой ненулевой цифрой в записи является семерка, поэтому стандартный вид будет выглядеть так:
7,6•10n
где n– какое-то целое число, которое нам надо найти. Поставим в исходном числе запятую после семерки:
7,6000000
Видно, что мы отделили запятой 7 разрядов, то есть перенесли запятую на 7 разрядов вправо. Поэтому n равно 7:
76000000 = 7,6•107
Действительно, умножение дробного числа на 10 приводит к смещению запятой на одну позицию влево, поэтому при умножении 7,6 на 107 получим 76000000. Наши действия можно проиллюстрировать рисунком:
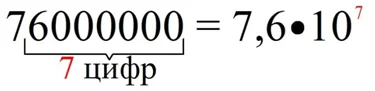
В случае с числами, меньшими единицы, также надо смотреть на количество разрядов между запятой и первой ненулевой цифрой. Пусть надо представить в стандартном виде десятичную дробь 0,000005605. Значащей частью числа будет 5,605. Для того чтобы получить ее, надо в исходной дроби перенести запятую на 6 разрядов вправо. Поэтому порядок будет равен (– 6):
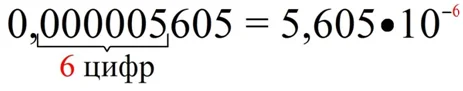
Теперь попробуем выполнить обратное преобразование – по стандартному виду числа записать его в привычной нам десятичной форме. Пусть есть запись 2,56•105. Для начала искусственно припишем несколько ноликов к значащей части:
2,56 = 2,5600000
Теоретически мы можем дописать любое количество нулей, величина дроби от этого не изменится. Порядок числа равен 5, а потому запятую надо перенести на 5 знаков вправо:
2,5600000•105 = 256000,00
Теперь лишние нули после запятой и саму запятую можно и убрать:
256000,00 = 256000
Обратите внимание, что порядок числа был равен 5, а в итоге мы получили шестизначное число. Можно сформулировать правило: у числа, имеющего в стандартной виде порядок n, в десятичной представлении перед запятой будет стоять (n + 1)знак
Например:
1,23456789•106 = 1234567,89
Здесь порядок числа равен 6, а потому перед запятой стоит 7 знаков.
Напомним, что если число целое и, соответственно, в его записи нет запятой, то ее можно искусственно добавить:
568 = 568,0
Теперь рассмотрим похожий пример с отрицательным порядком числа. Пусть надо записать в десятичном виде число 9,8765•10– 4. Для этого сначала можно условно «подрисовать» нолики перед значащей частью:
0000009,8765
Порядок равен (– 4), а потому надо передвинуть запятую на 4 знака влево
0000009,8765 =000,00098765
Получается, что мы подрисовали слишком много ноликов. Уберем два из нихи получим число в обычной форме:
0,00098765
Вообще, если у числа отрицательный порядок (– n), то первая ненулевая цифра должна оказаться на n-ой позиции после запятой:
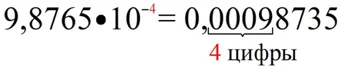
Понятие комплексного числа
Прежде чем, мы перейдем к рассмотрению комплексных чисел, дам важный совет: не пытайтесь представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве.
Если хотите, комплексное число – это двумерное число. Оно имеет вид , где и – действительные числа, – так называемая мнимая единица. Число называется действительной частью () комплексного числа , число называется мнимой частью () комплексного числа .
– это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: или переставить мнимую единицу: – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке:
Чтобы всё было понятнее, сразу приведу геометрическую интерпретацию. Комплексные числа изображаются на комплексной плоскости: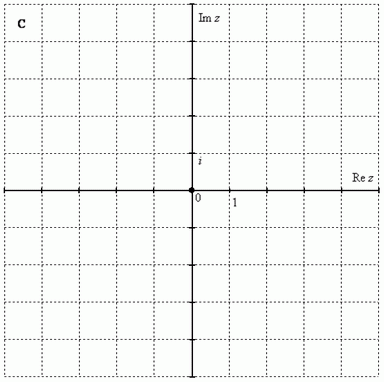
Как упоминалось выше, буквой принято обозначать множество действительных чисел. Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой . Поэтому на чертеже следует поставить букву , обозначая тот факт, что у нас комплексная плоскость.
Комплексная плоскость состоит из двух осей: – действительная ось – мнимая ось
Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат (см. Графики и свойства элементарных функций). По осям нужно задать масштаб, отмечаем:
ноль;
единицу по действительной оси;
мнимую единицу по мнимой оси.
Не нужно проставлять все значения: …–3, –2, –1, 0, 1, 2, 3,… и .
Да чего тут мелочиться, рассмотрим чисел десять.
Построим на комплексной плоскости следующие комплексные числа:, , , , , , ,
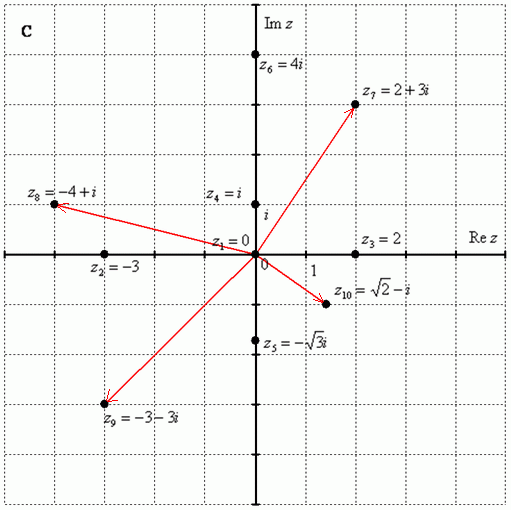
По какому принципу отмечены числа на комплексной плоскости, думаю, очевидно – комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии.
Рассмотрим следующие комплексные числа: , , . Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось обозначает в точности множество действительных чисел , то есть на оси сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел является подмножеством множества комплексных чисел .
Числа , , – это комплексные числа с нулевой мнимой частью.
Числа , , – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси .
В числах , , , и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, потому что они сливаются с осями.
Способ приведения одночлена к стандартному виду
Как привести моном к стандартной форме?
Из определения следует, что моном нестандартной формы является произведением чисел, переменных и их степеней, причем возможно их повторение. С другой стороны, стандартный одночлен в записи содержит только одно число и неповторяющиеся переменные или их степени.
Что значит привести моном к стандартной форме? Чтобы преобразовать нестандартный моном в стандартную форму, используйте следующее правило для преобразования монома в стандартную форму:
- первый шаг в том, как написать одночлен в стандартной форме, состоит в том, чтобы выполнить группировку числовых множителей, одинаковых переменных и их степеней;
- второй шаг в том, как стандартизировать моном, состоит в том, чтобы вычислить произведения чисел и использовать свойство степеней с тем же самым основанием.
Примеры и их решение
Пример 1
Дан моном 3 х 2 х 2. Необходимо привести его к стандартному виду.
Решение
Выполним группировку числовых множителей и множителей с переменной x, в результате заданный моном будет иметь вид: (3 2) (x x2).
Произведение в скобках равно 6. Используя правило умножения степеней с одинаковым основанием, выражение в скобках можно представить в виде: x1+2=x3. В итоге получаем одночлен стандартного вида: 6 х3.
Краткий обзор решения выглядит так: 3 x 2 x2=(3 2) (x x2)=6 x3.
Ответ: 3 х 2 х 2 = 6 х 3.
Пример 2
Дан моном: a5 b2 am (-1) a2 b . Необходимо привести его к стандартному виду и указать коэффициент.
Решение
данный одночлен имеет в записи один числовой множитель: -1, перенесем его в начало. Далее сгруппируем факторы с переменной а и факторы с переменной b.Переменную m группировать не с чем, оставляем в исходном виде. В результате вышеперечисленных действий получаем: -1 a5 a a2 b2 b m.
Проделайте операции со степенями в скобках, и моном будет иметь стандартный вид: (-1) a5+1+2 b2+1 m=(-1) a8 b3 m. Из этой записи легко определить коэффициент при моном: он равен — 1. Вполне можно просто заменить минус единицу знаком минус: (-1) a8 b3 m=-a8 b3 m.
Итог всех действий выглядит так:
a5 b2 am (-1) a2 b=(-1) (a5 a a2) (b2 b) m==(-1) a5+1+2 b2+1 m=(-1)a8 b3 m=-a8 б3 м
Отвечать:
a5 b2 am (-1) a2 b=-a8 b3 m, коэффициент данного одночлена равен -1.
Что такое стандартный вид одночлена и как привести выражение к нему
Для простоты все мономы сначала приводятся к особому виду, называемому стандартным. Давайте конкретизируем, что это означает.
Определение 2
Стандартной формой монома является его форма, где он представляет собой произведение числового множителя и натуральных степеней различных переменных. Численный множитель, также называемый мономиальным коэффициентом, обычно пишется первым с левой стороны.
Для наглядности выберем несколько одночленов стандартного вида: 6 (это одночлен без переменных), 4 a, −9 x2 y3 , 235 x7. Сюда же входят выражения xy (здесь коэффициент будет равен 1), −x3 (здесь коэффициент будет равен -1).
Теперь приведем примеры одночленов, которые необходимо привести к стандартному виду: 4 a a2 a3 (здесь надо совместить одинаковые переменные), 5 x (−1) 3 y2 (здесь надо сложить числовые множители слева).
Обычно в случае, когда одночлен имеет несколько переменных, записанных буквами, буквенные множители записываются в алфавитном порядке. Например, запись 6·a·b4·c·z2 предпочтительнее, чем b4·6·a·z2·c. Однако порядок может быть другим, если этого требует цель расчета.
Любой моном можно привести к стандартной форме. Для этого необходимо выполнить все необходимые идентичные преобразования.
Примеры («Запишите в стандартном виде»)
Представить числа а1, а2, а3, а4 в стандартном виде
а1 = 327 = 327,0 = 327 ∙ ∙102 = 3,27∙102 m = 2.
а2 = 0,3 = 0,3 ∙ 10 ∙ = 3∙10-1 m = -1
а3 = 0,37 = 0,37 ∙ 10 ∙ = 3,7∙10-1 m = -1
а4 = 1827 = 1827,0 = 1827 ∙ ∙ 1000 = 1,827∙103 m = 3
Еще раз посмотрим на структуру числа, записанного в стандартном виде, на примере вышерассмотренных чисел:
а0∙ 10m,
где а0є [1; 10), m є Z
3,27 ∙ 102, где 3,27 – а0
1,827 ∙ 103, где 1,827 – а0
3 ∙ 10-1, где 3 – а0
Стандартный вид числа удобен для записи больших и малых чисел.
Расстояние до Солнца составляет 150 000 000 км. Записать это число в стандартном виде.
а = 150 000 000км
а = 150000000,0 = 1,5∙108 m = 8
Записать число b = 0,000038 в стандартном виде.
b = 0,000038 = 3,8∙10-5 m = -5
Скорость света равна V = 300 000 км/с. Записать это число в стандартном виде.
V = 300000,0 = 3∙105
Ответ: V = 3∙105m = 5
1 световой год равен 30 860 000 000 000км. Записать это число в стандартном виде.
1с.г. = 30 860 000 000 000 = 3,086∙1013км m = 13
Вычислить и представить в стандартном виде.
1) (0,2∙105) ∙ (1,4∙10-2) = 0,28∙103 = 2,8∙10-1∙103 = 2,8∙102 m = 2
2) (0,004)2 = (4,0∙10-3)2 = 16∙10-6 = 1,6∙10∙10-6 = 1,6∙10-5 m = -5
Разряды и разрядность
Обратимся к табл. 4.6 и выпишем ряд десятичных чисел, которые равны “круглым” двоичным числам. В этот ряд входят следующие десятичные числа: “2”, “4”, “8”, “16”, “32”, “64”, “128”, “256”, “512” и, наконец, сакраментальное “1024”. Все эти числа представляют ряд последовательных степеней числа “2”. Каждое из названных чисел чрезвычайно активно используется в компьютерных технологиях. Читатель, видимо, убеждался в этом не один раз.
Мы оперируем каким-либо двоичным числом, а любое двоичное число – это совокупность битов, т. е. “1” и “0”. Отсюда получается, что каждый бит – это один разряд или одна позиция в двоичном числе.
ЗамечаниеНадеемся, что вы еще не забыли о позиционном принципе записи чисел в любых математических системах счисления (значение цифр, количество которых ограничено, зависит от положения в числе, от ее позиции).
В данный момент мы делаем шаг в сторону абстрагирования от конкретных значений цифр и начинаем считать только количество знакомест (позиций), которое в математике принято называть “разрядом”, а совокупность разрядов (знакомест) – “разрядностью”.
Определение
Разряд в арифметике – это место, занимаемое цифрой при записи числа. Например, в десятичной системе счисления цифры первого разряда – это единицы, второго разряда – десятки и т. д.
Но арифметические законы, которые кажутся привычными в десятичной системе счисления, все без исключения действительны и для двоичной системы счисления. Двоичные числа также можно складывать, вычитать, перемножать и делить с использованием тех же приемов школьного курса арифметики. Отличие заключается только в том, что используются всего две цифры.
Кроме того, как мы уже выяснили, в двоичной системе счисления каждый разряд – это бит и его значение зависит от позиции и равно соответствующей степени числа “2”.
Определение
Разрядность двоичного числа – это количество знакомест (разрядов) или количество битов, заранее отведенных для записи числа.
Пример
Десятичное число “2” может быть записано различными способами в зависимости от разрядности двоичного числа: как “10”, если разрядность равна двум; как “0010”, если разрядность равна четырем; как “00000010”, если разрядность равна восьми
Обратите внимание, что последний вариант соответствует записи десятичного числа “2” в пределах одного байта информации
Разрядность двоичного числа интересует нас в связи с тем, что это количество разрядов (позиций или знакомест) обеспечивает определенный набор возможных двоичных чисел, которые, как мы уже договорились, могут служить кодами, с помощью которых происходит кодирование любых видов информации: собственно чисел, текстов, графических и цветных изображений, звуков, анимации и видео.
Осталось только выяснить, каким образом разрядность влияет на количество информации (двоичных кодов), которую можно получить с помощью определенного количества разрядов. Однако прежде следует учесть одну особенность двоичных чисел, нашедшую применение в компьютерных технологиях, – это фиксированные значения разрядности двоичных чисел.
Запись дробных чисел
Стандартная запись дробей
Основное правило записи дробей — числитель и знаменатель дроби записываются через дробную черту. Например, 3/4 или 7/8. Также стандартным является запись десятичных дробей, где число отделяется запятой или точкой. Например, 0,5 или 2.3.
Порядок цифр
При записи дробных чисел в системе счисления с основанием 10, порядок цифр после запятой определяет дробную часть числа. Например, число 14,56 можно записать как 14 5/10 6/100 или как 14 + 5/10 + 6/100.
Дроби и умножение
В случае умножения дробей, числитель и знаменатель каждой дроби умножаются между собой. Например, 1/4 * 2/3 = 2/12. После этого дробь можно упростить.
Дроби и деление
В случае деления дробей, делимое умножается на обратную дробь делителя. Например, 3/4 : 1/2 = 3/4 * 2/1 = 6/4. Эту дробь можно упростить, например, до дроби 3/2.
Значение дроби и неравенства
Когда мы сравниваем значения двух дробей, мы можем сравнивать как числители, так и знаменатели каждой дроби. Если числители дробей одинаковы, то больше будет та дробь, у которой знаменатель меньше. Например, 3/4 > 2/4, так как 3 > 2, но также 2/4 < 3/4, так как 4 > 2.
Дроби в образовательной материале
Дроби широко используются в образовательной материале для решения задач, например, в геометрии для нахождения промежутков или в физике для вычисления степени пространственного продолжения. Они также используются в химии для определения количества массы элементов или в химических реакциях. Помимо этого, дроби используются в матричной алгебре для вычисления производной и в теории вероятностей для описания скоростей случайных событий.
Дроби в повседневной жизни
Дроби используются в повседневной жизни в самых разных ситуациях, например, при расчете скидок или при делении подарочных конфет между друзьями. Кроме того, дроби могут понадобиться при вычислении времени в единицах времени неравномерной длины, например, для нахождения скорости движения тела.
Возведение комплексных чисел в степень
Начнем со всеми любимого квадрата.
Пример 9
Возвести в квадрат комплексное число
Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.
Второй способ состоит в применении известной школьной формулы сокращенного умножения :![]()
Для комплексного числа легко вывести свою формулу сокращенного умножения:. Аналогичную формулу можно вывести для квадрата разности, а также для куба суммы и куба разности. Но эти формулы более актуальны для задач комплексного анализа, поэтому на данном уроке я воздержусь от подробных выкладок.
Что делать, если комплексное число нужно возвести, скажем, в 5-ю, 10-ю или 100-ю степень? Ясно, что в алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде ?
И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра: Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степень справедлива формула:
Данная формула следует из правила умножения комплексных чисел, представленных в тригонометрической форме: чтобы найти произведение чисел , нужно перемножить их модули и сложить аргументы:
Аналогично для показательной формы: если , то:
Просто до безобразия.
Пример 10
Дано комплексное число , найти .
Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:
Тогда, по формуле Муавра:![]()
Упаси вас, не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет радиан или 360 градусов. Выясним сколько у нас оборотов в аргументе . Для удобства делаем дробь правильной: , после чего становится хорошо видно, что можно убавить один оборот: . Надеюсь всем понятно, что и – это один и тот же угол.
Таким образом, окончательный ответ запишется так:
Любители стандартов везде и во всём могут переписать ответ в виде: (т.е. убавить еще один оборот и получить значение аргумента в стандартном виде).
Хотя – ни в коем случае не ошибка.
Пример 11
Дано комплексное число , найти . Полученный аргумент (угол) упростить, результат представить в алгебраической форме.
Это пример для самостоятельного решения, полное решение и ответ в конце урока.
Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.
Пример 12
Возвести в степень комплексные числа , ,
Здесь тоже всё просто, главное, помнить знаменитое равенство.
Если мнимая единица возводится в четную степень, то техника решения такова:
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:![]()
Пример 13
Возвести в степень комплексные числа ,
Это пример для самостоятельного решения.
Типы данных
Переменные разных типов имеют разные особенности и позволяют хранить числа в разных диапазонах.
| Название | Альт. название | Вес | Диапазон | Особенность |
| 1 байт * | 0 или 1, или | Логический тип | ||
| – | 1 байт | -128… 127 (AVR), 0.. 255 (esp) | Символ (код символа) из таблицы ASCII | |
| – | 1 байт | -128… 127 | Целые числа | |
| 1 байт | 0… 255 | Целые числа | ||
| ** | , | 2 байта | -32 768… 32 767 | Целые числа. На ESP8266/ESP32 – 4 байта! См. ниже |
| ** | , | 2 байта | 0… 65 535 | Целые числа. На ESP8266/ESP32 – 4 байта! См. ниже |
| 4 байта | -2 147 483 648… 2 147 483 647 | Целые числа | ||
| 4 байта | 0… 4 294 967 295 | Целые числа | ||
| – | 4 байта | -3.4E+38… 3.4E+38 | Числа с плавающей точкой, точность: 6-7 знаков | |
| – | 4/8 байт | -1.7E+308.. 1.7E+308 | Для AVR то же самое, что .
На ESP и прочих 32-бит МК – 8 байт, точность – 15-16 знаков |
|
| – | 8 байт *** | -(2^64)/2… (2^64)/2-1 | Целые числа | |
| – | 8 байт *** | 2^64-1 | Целые числа |
- (*) – да, занимает 1 байт (8 бит), так как это минимальная адресуемая ячейка памяти. Есть способы запаковать логические переменные в 1 бит, о них поговорим в другом уроке.
- (**) – на ESP8266/ESP32 и занимает 4 байта, то есть является аналогами типов и !
- (***) – Компилятор также поддерживает 64 битные числа. Стандартные Arduino-библиотеки с переменными этого типа не работают, поэтому можно использовать только в своём коде.
Целочисленные типы
Переменные целочисленных типов нужны для хранения целых чисел. В своей программе рекомендуется использовать альтернативное название типов (второй столбец в таблице выше), потому что:
- Проще ориентироваться в максимальных значениях
- Легче запомнить
- Название более короткое
- Проще изменить один тип на другой
- Размер переменной задан жёстко и не зависит от платформы (например на AVR это 2 байта, а на esp8266 – 4 байта)
Максимальные значения хранятся в константах, которые можно использовать в коде. Иногда это помогает избавиться от лишних вычислений:
- – 255
- – 127
- – 65 535
- – 32 767
- – 4 294 967 295
- – 2 147 483 647
- – 18 446 744 073 709 551 615
- – 9 223 372 036 854 775 807
Логический тип
– логический, он же булевый (придуман Джорджем Булем) тип данных, принимает значения и или и – ложь и правда. Используется для хранения состояний, например включено/выключено, а также для работы в условных конструкциях.
Также переменная типа принимает значение , если присвоить ей любое отличное от нуля число.
bool a = 0; // false bool b = 1; // true bool c = 25; // true
Символьный тип
– тип данных для хранения символов, символ указывается в одинарных кавычках: . По факту это целочисленный тип данных, а переменная хранит номер (код) символа в таблице ASCII:
Отдельный символьный тип данных нужен для удобства работы, чтобы программа могла понять разницу между числом и символом, например для вывода на дисплей (чтобы вывести именно букву A, а не число 65). Из символов можно составлять строки, об этом более подробно поговорим в уроках про символьные строки и String-строки.
Символы и числа
Несмотря на то, что в языке Си символ это по сути целое число, значения например и не равны между собой, потому что символ с точки зрения программы является числом . На практике иногда бывает нужно конвертировать символы чисел в соответствующие им целые числа и наоборот (при работе со строками и буферами вручную), для этого распространены следующие алгоритмы:
- Из символа в число – взять младший ниббл (4 бита):
- Из символа в число – вычесть символ 0:
- Из числа в символ – прибавить символ 0:
Дробные числа
(англ. float – плавающий) – тип данных для чисел с плавающей точкой, т.е. десятичных дробей. Arduino поддерживает три типа ввода чисел с плавающей точкой:
| Тип записи | Пример | Чему равно |
| Десятичная дробь | 20.5 | 20.5 |
| Научный | 2.34E5 | 2.34*10^5 или 234000 |
| Инженерный | 67e-12 | 67*10^-12 или 0.000000000067 |
Выше в таблице есть пометка “точность: 6-7 знаков” – это означает, что в этом типе можно хранить числа, размер которых не больше 6-7 цифр, остальные цифры будут утеряны! Причём целой части отдаётся приоритет. Вот так это выглядит в числах (в комментарии – реальное число, которое записалось в переменную):
float v; v = 123456.654321; // 123456.656250 v = 0.0123456789; // 0.0123456788 v = 0.0000123456789; // 0.0000123456788 v = 123456789; // 123456792.0
Другие особенности float чисел и работу с ними мы рассмотрим в уроках про математические операции и условия.






























