Таблица деления для 2-3 классов

Секреты устного счёта

Существуют приемы устного счета — простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.

Прибавляем числа 7,8,9

Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.

Примеры:

56+7=56+10-3=63

47+8=47+10-2=55

73+9=73+10-1=82

Быстро складываем двузначные числа

Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».

Примеры:

54+39=54+40-1=93

26+38=26+40-2=64

Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем — единицы.

Пример:

57+32=57+30+2=89

Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:

32+57=32+60-3=89

Складываем в уме трехзначные числа

Быстрый счет и сложение трехзначных чисел — это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.

Пример:

249+533=(200+500)+(40+30)+(9+3)=782

Особенности вычитания: приведение к круглым числам

Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.

Примеры:

67-9=67-10+1=58

576-88=576-100+12=488

Вычитаем в уме трехзначные числа

Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.

Пример:

843-596=843-500-90-6=343-90-6=253-6=247 

Умножить и разделить

Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения — это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения — с 11 до 19!

Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:

15*16=15*10+(10*6+5*6)=150+60+30=240

Умножаем и делим на 4, 6, 8, 9

Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.

Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:

• умножить на 4 — это дважды умножить на 2;

• умножить на 6 — это значит умножить на 2, а потом на 3;

• умножить на 8 — это трижды умножить на 2;

• умножить на 9 — это дважды умножить на 3.

Например:

37*4=(37*2)*2=74*2=148;

412*6=(412*2)·3=824·3=2472

Аналогично:

• разделить на 4 — это дважды разделить на 2;

• разделить на 6 — это сначала разделить на 2, а потом на 3;

• разделить на 8 — это трижды разделить на 2;

• разделить на 9 — это дважды разделить на 3.

Например:

412:4=(412:2):2=206:2=103

312:6=(312:2):3=156:3=52

Как умножать и делить на 5

Число 5 — это половина от 10 (10:2). Поэтому сначала умножаем на 10, затем полученное делим пополам.

Пример:

326*5=(326*10):2=3260:2=1630

Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.

326:5=(326·2):10=652:10=65,2.

Умножение на 9

Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:

37*9=(37*3)*3=111*3=333

или

37*9=37*10 — 37=370-37=333

Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма. Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко — это примеры занимательные, так называемые маленькие хитрости.

О. Наумова «Учим таблицу умножения. Большой тренажер»

Бесценный богатый тренажер!В книге вы найдете:

• 110 страниц интересных результативных упражнений;
• разнообразные задания;
• творческий подход;
• нестандартные приемы;
• задания разного уровня сложности;
• различные шифровки;
• игры и раскраски.

Ваш ребенок получит:

• легкое и без нервов запоминание таблицы умножения;
• развитие внимания и мышления;
• улучшение в целом математических способностей;
• огромное количество интересных и полезных заданий.

Книга может быть использована как для индивидуальной работы, так и работы в классе.Скучно точно не будет!

Тренажер удобен для распечатывания!

Считаем уникальные значения в столбце.

Предположим, у вас есть столбец с именами на листе Excel, и вам нужно подсчитать, сколько там есть неповторяющихся. Самое простое решение состоит в том, чтобы использовать функцию СУММ в сочетании с ЕСЛИ и СЧЁТЕСЛИ :

Примечание. Это формула массива, поэтому обязательно нажмите Ctrl + Shift + Enter, чтобы корректно ввести её. Как только вы это сделаете, Excel автоматически заключит всё выражение в {фигурные скобки}, как показано на скриншоте ниже. Ни в коем случае нельзя вводить фигурные скобки вручную, это не сработает.

В этом примере мы считаем уникальные имена в диапазоне A2: A10, поэтому наше выражение выглядит так:

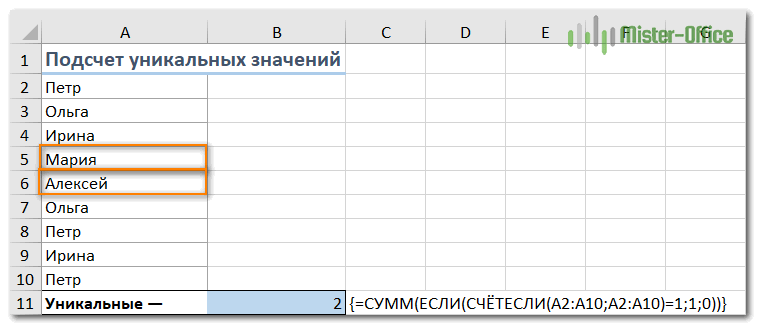
Этот метод подходит и для текстовых, и для цифровых данных. Недостатком является то, что в качестве уникального он будет пересчитывать любое содержимое, в том числе и ошибки.

Далее в этом руководстве мы обсудим несколько других подходов для подсчета уникальных значений разных типов. И поскольку в основном они являются вариациями этой базовой формулы, имеет смысл подробно рассмотреть её. Если вы поймете, как это работает, то сможете настроить ее для своих данных. Если кого-то не интересуют технические подробности, вы можете сразу перейти к следующему примеру.

Как работает формула подсчета уникальных значений?

Как видите, здесь используются 3 разные функции – СУММ, ЕСЛИ и СЧЁТЕСЛИ. Посмотрим, что делает каждая из них:

Функция СЧЁТЕСЛИ считает, сколько раз каждое отдельное значение появляется в анализируемом диапазоне.

В этом примере СЧЁТЕСЛИ(A2:A10;A2:A10)возвращает массив {3:2:2:1:1:2:3:2:3}.

Функция ЕСЛИ оценивает каждый элемент в этом массиве, сохраняет все единицы (то есть, уникальные) и заменяет все остальные цифры нулями.

Итак, функция ЕСЛИ(СЧЁТЕСЛИ(A2:A10;A2:A10)=1;1;0) преобразуется в  ЕСЛИ({3:2:2:1:1:2:3:2:3}) = 1,1,0).

И далее она превращается в массив чисел  {0:0:0:1:1:0:0:0:0}. Здесь 1 означает уникальное значение, а 0 – появляющееся более 1 раза.

Наконец, функция СУММ складывает числа в этом итоговом массиве и выводит общее количество уникальных значений. Что нам и нужно.

Целенаправленное запоминание

После того, как ваш ребенок освоил самые простые значения таблицы умножения, можно приступать к более сложным множителям

Тут важно использовать и элементы игры, и многие другие полезные приемы запоминания: ассоциации, повторение, дробление на части, проверочные задачки, применение на практике. Многие из примеров нужно будет заучивать, запоминать и повторять неоднократно, чтобы ваш ребенок смог потом с легкостью называть значения таблицы умножения. Лучше идти по порядку, и не пытаться выучить все сразу

Начать лучше с квадратов и умножения на 3 и 4, постепенно переходя к остальным числам

Лучше идти по порядку, и не пытаться выучить все сразу. Начать лучше с квадратов и умножения на 3 и 4, постепенно переходя к остальным числам.

Некоторые педагоги считают правильным способом начать изучение таблицы умножения с конца от более сложных примеров к более простым. Но лучше так не делать, чтобы избежать стресса ребенка от непонимания того, как эти значения были получены. Умножая 3 на 3, ребенок может проверить себя на пальцах, и убедиться, почему в таблице умножения стоит именно 9. А если ему сразу предложить умножить 8 на 9, и сказать, что результат нужно просто запомнить, он не сможет применить свои знания на практике, что ухудшит запоминание и может отрицательно сказаться на его мотивации.

Квадраты чисел. Квадратом числа называется его произведение на самого себя. В русской таблице умножения есть всего 10 квадратов, которые нужно запомнить. Квадраты до примера «шесть на шесть тридцать шесть» обычно запоминаются на ура, и следующие 3 квадрата обычно тоже не вызывают особых трудностей. А 10 на 10 – будет сто, что мы уже проходили ранее на предыдущих уроках.

Таблица умножения на 3. Именно на этом этапе могут возникнуть первые сложности. Если так случилось, что ребенок не может запомнить какие-то значения, то самое время начать использовать карточки. А если это не помогает, и вы знаете, что у вашего чада больше гуманитарный склад ума, то можете попробовать (о них еще будет написано ) для запоминания таблицы умножения.

Таблица умножения на 4. Здесь также можете использовать карточки и стихи. Кроме того, дайте ребенку понять, что умножение на четыре — это то же самое, что и умножение на 2 и еще раз на 2. Эти и другие простейшие арифметические закономерности, которые могут быть полезны для развития устного счета, вы найдете в данной статье.

Таблица умножения на 5. Умножение на пять обычно дается просто. Интуитивно ребенку становится понятно, что все значения этого умножения расположены через 5 друг от друга и заканчиваются либо на 5, либо на 0. Все четные числа, умноженные на 5, всегда оканчиваются на ноль, а нечетные – оканчиваются на 5.

Таблица умножения на 6, 7, 8 и 9. Есть определенная особенность изучения сложных примеров из таблицы умножения. Если ребенок выучил квадраты, а также таблицу умножения до 5, то на самом деле ему осталось выучить совсем немного, так как остальные примеры он уже знает

Это хорошо видно на этой таблице умножения, где зеленым выделены ячейки, уже освоенные ребенком к данному моменту

В итоге, оставшиеся клетки таблицы умножения содержат всего шесть произведений, которые и являются самыми сложными, и на которые стоит обратить пристальное внимание

1. 6×7=42
2. 6×8=48
3. 6×9=54
4. 7×8=56
5. 7×9=63
6. 8×9=72

Для запоминания этих выражений таблицы умножения лучше использовать игру в карточки, чтобы довести ответы до автоматизма. Эффективнее всего использовать 12 карточек (с переменой мест множителей). Как показывает практика, у школьников, а часто и у взрослых, именно с этими шестью произведениями часто бывают некоторые проблемы.

Вот и все! Всего за несколько уроков вся таблица умножения может быть легко и быстро выучена!

С чего начать изучение таблицы умножения?

Первый этап подготовки выполните сами – распечатайте таблицу Пифагора и таблицу с примерами

И вот тут важно обратить внимание, что это не одно то же. Во втором случае это просто примеры с готовыми ответами, представленные в столбиках для каждой цифры. Первый вариант и является настоящей таблицей умножения (Пифагора), которая представлена сеткой 10х10

Первый вариант и является настоящей таблицей умножения (Пифагора), которая представлена сеткой 10х10

Это отличный способ, как легко запомнить таблицу умножения

Первый вариант и является настоящей таблицей умножения (Пифагора), которая представлена сеткой 10х10. Это отличный способ, как легко запомнить таблицу умножения.

Прежде чем выучить наизусть всю таблицу умножения ребенку, покажите ему, что цифры, которые перемножаются, находятся слева и сверху, а если пальчиками от них провести навстречу друг другу, то на пересечении будет результат их перемножения.

Задаваясь вопросом, как быстро выучить таблицу умножения ребенку, и с чего начать этот процесс, то знакомить его с самими действиями нужно, начиная с тех манипуляций с умножением, которые ему понять и выполнить самостоятельно будет проще всего:

• На «1». Любое действие в этом случае дает результат, при котором число остается прежним. Так школьнику будет проще понимать, что это за процесс. Предложите ему попрактиковаться с умножением на один несколько раз с разными числами;
• На «10». Объясните ребенку, что, несмотря на то что это большое число, умножать на него очень просто. Нужно лишь к умножаемому приписывать ноль. Начните с небольших значений – например, 3х10, а потом предложите ему самостоятельно попробовать выполнить действия с большими числами.

На пути к тому, как научить быстро выучить таблицу умножения ребенка, это важные шаги. Теперь он знает, как работать с крайними значениями сетки Пифагора. Помимо практического значения, для него это играет и психологическую роль:

• у школьника сложится понятие того, как нужно работать с ней;
• он поймет, что начало положено, и ему знакомиться с сеткой не сложно, даже интересно, поэтому полностью ее освоить он сможет.

Если ученик еще не устал, можно приступать к следующему этапу того, как можно быстро выучить таблицу умножения:

предложите школьнику умножать на «2». Уже с первых классов обучения математике дети знают, как выполнять сложение до 10, в том числе одинаковых чисел. Поэтому занятие будет для обучаемого простым и даже интересным; перемена мест множителей

Это важное правило, часто непонятное детям, заключающееся в том, что при перестановке множителей их произведение остается прежним. Обязательно покажите это на самой сетке в соответствующих графах. Благодаря этому ребенку проще будет запомнить это правило, называемое коммутативным или переместительным

К тому же, так он быстрее запомнит определенные действия умножения и их произведения

Благодаря этому ребенку проще будет запомнить это правило, называемое коммутативным или переместительным. К тому же, так он быстрее запомнит определенные действия умножения и их произведения.

Это первые шаги, применяя которые вы положите начало запоминанию и к тому, чтобы быстро и просто потом выучить действия и результаты, указанные в сетке.

как выучить таблицу умножения

Подготовка к изучению таблицы умножения

Этот этап является в том числе организационным, но он входит в алгоритм того, как легко выучить таблицу умножения и сделать это быстро. Подготовка включает в себя такие шаги:

• подберите время, когда вы ежедневно будете заниматься с ребенком. Учитывайте, что на изучение нужно уделять не менее 30 минут (это длительность одного занятия). Поэтому в это время ученик не должен быть уставшим, но должен быть готов к эффективному обучению;
• приготовьтесь к тому, что процесс этот должен включать игровой момент, потому что игра – легкий способ выучить таблицу умножения;
• саму сетку или столбики с примерами вы можете распечатать, а можете расчертить самостоятельно;
• продумайте, как и когда, в какое время вы будете проверять выученный материал.

Помогите вашему ребенку выучить таблицу умножения: с чего начать

Если ваш ребенок уже сталкивался с таблицей умножения — видел, задавал вопросы, пробовал применить

• Объясните сыну или дочке, что такое количество цифр не должно пугать: не придется заучивать все наизусть
• В таблице умножения есть определенные логические закономерности.
• Дайте понять, что вы не собираетесь заставлять бездумно зубрить числа, но поможете увидеть связь между ними.

Если ребенок до этого не видел таблицу

Купите или распечатайте плакат с ней и повесьте над рабочим столом, чтобы школьник привык к ее виду. Даже если ребенок визуально знаком с таблицей, лучше все равно украсить ей детскую зону. Предлагаем несколько таких плакатов для распечатывания.

Примеры плакатов с таблицей умножения

Ребенок сопротивляется или просто не понимает, в чем смысл умножения?

Объясните, что это более короткая запись уже того, что он знает — сложения. Это станет первым шагом к снижению тревожности из-за нового учебного материала.

Покажите, что 2+2 — то же самое, что 2*2, а 3+3+3 можно спокойно заменить на 3*3 и так далее.

Наконец, перед реальными математическими занятиями вместе с ребенком через умножение:

1. Попробуйте считать количество конфет в коробке;
2. Количество предметов в недельном расписании;
3. Количество колес на всех игрушечных машинках или рук и ног у кукол — на что хватит фантазии.

Как заполнять бланк регистрации ЕГЭ

Состоит из 3-х частей.

1) Верхняя часть бланка:

Штрихкоды – важная часть бланка. Не заляпайте их чернилами, будут проблемы.

Недавно выпускникам немного упростили жизнь: все серые поля заполнятся автоматически при печати. Хотя бы тут не ошибемся.

Однако, если ваши бланкипривезут в пункт проведения ЕГЭ, а не распечатают на месте, заполненными будут только Код предмета, Название и Дата экзамена.

Поэтому, ВОЗМОЖНО, придётся заполнить:

• Код региона – Федеральный код региона, в котором вы сдаете экзамен. Например, в Москве это 77, а в Бурятии – 03. Узнайте заранее свой в справочнике, а потом сверьте с тем, что напишут на доске.
• Код пункта проведения ЕГЭ– код школы, в которую вы приехали сдавать экзамен. Нет, с ее номером не совпадает. Переписывайте с доски внимательно.

Эти 3 поля нужно заполнить самостоятельно

ТОЧНО придётся заполнить:

Код образовательной организации. Нет, это не номер вашей школы. У каждого образовательного учреждения есть собственный код. Мы знаем четыре варианта, как его узнать:

1. спросить в своей школе,
2. посмотреть в уведомлении участника ЕГЭ,
3. прочитать рядом со своей фамилией на двери аудитории перед экзаменом, 
4. спросить у наблюдающих во время заполнения бланков.

Вам обязательно помогут вписать код своей школы.

• Класс. Номер и буква вашего класса. Хотя в правилах написано, что участники ЕГЭ это поле не заполняют. Так что уточняйте у наблюдателей!
• Номер аудитории. Номер класса, куда вас посадили. Эта информация для всех в аудитории одинаковая, сверяйтесь с образцом на доске. «>

[Уильям Ховард Тафт сидит за столом, играет в карты со своей женой и двумя мужчинами на лодке по пути на Филиппины] — черно-белая копия фильма, отрицательная.

Подробнее об авторских правах и других ограничениях

Для получения рекомендаций по составлению полных ссылок обращайтесь
Ссылаясь на первоисточники.

• Консультант по правам :
  Нет известных ограничений на публикацию.
• Репродукция номер :
  LC-USZ62-132301 (черно-белая копия на пленке, отрицательная)
• Телефонный номер :
  Необработано в PR 13 CN 1980:167
• Консультативный доступ :
  —

Получение копий

Если отображается изображение, вы можете загрузить его самостоятельно. (Некоторые изображения отображаются только в виде эскизов за пределами
Библиотеке Конгресса из соображений прав, но у вас есть доступ к изображениям большего размера на
сайт.

Кроме того, вы можете приобрести копии различных типов через
Услуги тиражирования Библиотеки Конгресса.

1. Если отображается цифровое изображение: Качества цифрового изображения частично
   зависит от того, был ли он сделан из оригинала или промежуточного звена, такого как копия негатива или
   прозрачность. Если поле «Репродукционный номер» выше включает репродукционный номер, начинающийся
   с LC-DIG…, то есть цифровое изображение, которое было сделано непосредственно с оригинала
   и имеет достаточное разрешение для большинства целей публикации.
2. Если в поле Номер репродукции выше указана информация: Вы можете использовать репродукционный номер для покупки копии в Duplication Services. Это будет
   сделано из источника, указанного в скобках после номера.

   Если в списке указаны только черно-белые («ч/б») источники и вам нужна копия, показывающая
   цвета или оттенка (при условии, что они есть у оригинала), обычно можно приобрести качественную копию
   оригинал в цвете, указав номер телефона, указанный выше, включая каталог
   запись («Об этом элементе») с вашим запросом.

3. Если в поле Номер репродукции выше нет информации: Как правило, вы можете приобрести качественную копию через Duplication Services. Назовите номер телефона
   перечисленных выше, и включите запись каталога («Об этом элементе») в свой запрос.

Прайс-листы, контактная информация и формы заказа доступны на
Веб-сайт службы дублирования.

Доступ к оригиналам

Выполните следующие действия, чтобы определить, нужно ли заполнять бланк вызова в разделе «Печать».
и читальный зал фотографий, чтобы просмотреть исходные предметы. В некоторых случаях используется суррогатное изображение (замещающее изображение).
доступны, часто в виде цифрового изображения, копии или микрофильма.

Устный счёт на автомате

• Во-первых, необходимо хорошо знать состав числа и таблицу умножения.

• Во-вторых, надо запомнить приемы упрощения расчётов. Как выяснилось, таких математических алгоритмов не так уж много.

В-третьих, чтобы приём превратился в удобный навык, надо постоянно проводить краткие «мозговые штурмы» — упражняться в устных вычислениях, используя тот или иной алгоритм.

Тренировки должны быть короткими: решить в уме по 3-4 примера, используя один и тот же приём, затем переходить к следующему. Надо стремиться использовать любую свободную минутку — и полезно, и нескучно. Благодаря простым тренировкам все вычисления со временем будут совершаться молниеносно и без ошибок. Это очень пригодится в жизни и выручит в непростых ситуациях.

Кто составляет расчетный лист

Расчетный лист составляет специалист отдела бухгалтерии, т.е. сотрудник, который имеет полные данные обо всех полагающихся тому или иному работнику выплатах. Что характерно, заверять лист подписью руководителя компании или хотя бы даже самого бухгалтера необязательно, как и проставлять на нем печать.

Связано это с тем, что лист носит сугубо информационный характер, иными словами, он никак не подтверждает факт получения именно той суммы заработной платы, которая в нем была обозначена к выплате.

А вот что касается работника организации, то он в получении расчетного листка расписаться должен. Для этого бухгалтер или кассир может предоставить ему специальный бланк под названием «лист выдачи расчетных листков».

Этап первый «Что такое умножение»

Начинать изучать таблицу умножения надо с объяснения самих принципов данного действия. Малыш должен понять, что умножение – это всего лишь сложение некоторого количества одинаковых слагаемых.

Лучше всего объяснение проводить на понятных малышу примерах, а не просто расписать на бумаге математические формулы. К примеру, можно задать своему чаду такую задачку: «Мама и папа взяли из вазочки по 3 конфеты. Сколько конфет они взяли вместе?». При этом для наглядности лучше использовать настоящие конфеты. Сложив 3+3, ребёнок скажет нужный ответ. Теперь осталось объяснить ему, что сложение можно заменить и умножением (2*3 это тоже самое, что 3+3). Далее задачку следует усложнить, пусть столько же конфет возьмёт ещё и братик или сестричка. И снова пример: 3+3+3 или 3*3. При желании можно инсценировать целый спектакль, задействовав игрушки и любимые лакомства. И не беда, если ребёнок сразу не понял принципы умножения – обучение у всех проходит с разной скоростью. В конце концов, он разберётся. Главное, не злиться и не форсировать события. В противном случае малыш просто откажется заниматься.

Эффективно ли решение Таблиц Шульте?

Через методику специалисты отслеживали работоспособность и скорость ориентировочно-поисковых движений взгляда. Однако, после публикации данного метода, он приобрел популярность в более широких кругах психиатров и психотерапевтов. В ходе исследований была доказана высокая эффективность занятий для развития памяти, внимания, и интеллекта, в целом

При регулярном решении подобных задач, вне зависимости от возраста (заниматься может как школьник, так и взрослый), улучшается объемное внимание. Все дело в самой методике: когда символы воспринимаются сразу все вместе, а отыскиваются последовательно

Впоследствии их стали активно использовать во всевозможных курсах по развитию скорочтения и для расширения поля зрения, в целом.

В работах некоторых специалистов в области психиатрии и психологии внимание уделено и им.  Состояние человека, который занимается поиском символов схоже с состоянием, которое достигается во время сеанса медитации. А подобные состояния позволяют не только “перезагрузить голову”

Они положительно сказываются на всех областях нашего мозга.

Часто можно встретить случаи, когда таблицы Шульте являлись частью курсов по НЛП. Но как связаны Нейролингвистическое Программирование и эти задачи? Сознание перестраивается. Оно переключается от критического и избирательного восприятия к некоему апатичному состоянию, тем самым повышая способность мозга решать последовательные логические задачи.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

8*4=8+8+8+8=32

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Таблица умножения

Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

• 79*50=(70+9)*50=3500+450=3950
• 79*7=(70+9)*7=490+63=553
• 3950+553=4503

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.

Проверим и умножим 54 на 11.

• 5+4=9
• 54*11=594

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число 75.

• 7*8=56
• 5*5=25
• 75*75=5625

Раньше все считали без калькуляторов

🔲 Ведический квадрат

Понятие ведического квадрата известно из индийской математики, где он является вариацией обычной таблицы умножения 9 х 9. Запись в каждой ячейке – это цифровой корень произведения заголовков столбцов и строк, и этот же корень представляет собой остаток, получаемый при делении произведения заголовков строк и столбцов на 9.

Если говорить максимально просто, то в ведическом квадрате любой результат перемноженных чисел сведен к однозначному значению от 1 до 9. Например, 7 × 6 = 42 = 6, а 8 х 6 = 48 = 12 = 3:

Это делает ведический квадрат поистине уникальным явлением. Несложно заметить, что числа от 1 до 9, которые заполняют его клетки, повторяются определенным образом. Кроме 3, 6 и 9, все остальные числа занимают по шесть клеток, числа 3 и 6 занимают по двенадцать клеток, а число 9 повторяется 21 раз.

Однако истинная работа с ведическим квадратом – это не просто умножение или деление, а произведение сложнейших вычислений из области модульной арифметики, теории категорий, абстрактной алгебры, теоретической информатики, моноидов и других алгебраических структур.

Мало того, в ведическом квадрате можно наблюдать огромное количество симметрий и геометрических узоров, некоторые из которых можно отследить в традиционном индийском и исламском искусстве (если соединить повторяющиеся числа, на выходе получится диаграмма или вполне определенный узор):

А еще этот квадрат используется в нумерологии, ведь он считается примером древнего знания, дошедшего до современного человека, в котором числа являют собой посланников космической энергии. Вот так могут выглядеть нумерологические вычисления (они вам уже знакомы):

2 × 1 = 2
2 × 2 = 4
2 × 3 = 6
2 × 4 = 8
2 × 5 = 10 = 1
2 × 6 = 12 = 3
2 × 7 = 14 = 5
2 × 8 = 16 = 7
2 × 9 = 18 = 9

Сегодня ведический квадрат не пользуется большой популярностью среди обывателей, но в Древней Индии он имел колоссальное значение. Сейчас же, как мы и сказали, он более распространен в нумерологии и, по мнению ее приверженцев, помогает улучшать жизни многих людей по всему миру.

Уверены, вы смогли заметить, что таблица умножения и содержащиеся в ней цифры – это в некоторой степени нечто магическое. Однако практическое их применение – вовсе не магия, а использование в повседневных делах, работе, учебе или бизнесе.

Вариантов таблицы умножения существует немало, и есть и те, о которых мы сегодня не рассказали, но все они говорят об одном – уметь умножать, делить и производить другие вычисления важно и нужно всем, а уж каким образом это делать – личный выбор каждого из нас