Символы, обозначения, понятия школьного курса математики (антипов, шварцбурд) 1978 год

Перенос

Для использования чисел еще рановато, но мы уже близко. Возьмем вместо них пока нечто попроще и породнее. Алисе я бы посоветовал посмотреть на пальцы. Ну а для «пастуха» — пальцев будет маловато. Но всегда можно найти объект поменьше коровы, который можно поместить в руках, например, камешки. И что нужно с ними сделать? Правильно сопоставить! Палец сопоставим слову «один». А камешек сопоставим одной корове. Легко сказать «сопоставить». А каким алгоритмом это можно сделать?

У Алисы ситуация проще. На каждое услышанное слово «один» достаточно «комплементарно» загнуть один палец на своих руках. Для «пастуха» это сопоставление чуть сложнее, но принцип схож. Стадо тоже необходимо выстроить в структуру — и лучше всего использовать структуру линейную, совсем как у слов «один» во фразе Королевы. Например, это можно сделать утром, когда коровы выходят из коровника с узкой дверью, пропускающей за раз только одну корову. Необходимо заранее запастись камешками. И для каждой выходящей коровы брать камешек и «загнуть его», ну, нет, конечно, это же не палец Алисы. Нужно положить его в отдельное выбранное место. Так формируется кучка камней. И когда последняя корова выйдет, в кучке будет лежать столько же камней сколько коров в стаде. А зачем нам эти загнутые пальцы и кучка камней? Правильно! С ними проще работать, чем с растворяющейся в памяти длинной фразой или большим стадом. С ними можно выполнить подсчет. С кучкой камней легко придумать алгоритм формирования запаса сена на зиму в отдельном от коровника хранилище. И можно выполнить много еще чего. Мы Перенесли опору алгоритма запаса сеном на зиму с использования коров на использование камешков. И упростили жизнь «пастуху», сделав его уже немного «математиком».

До серьезного математика остался один шаг. Этот шаг — появление операции сложения. И шаг прост. Например, нужно, два «пастуха», хранящих в кармане кучки камешков, которые соответствуют каждая своему стаду. При этом достаточно только возникновения ситуации, когда два стада нужно объединить. В этом случае, конечно, можно прогнать полученное объединенное стадо через коровник с узкой дверью. Но ведь гораздо проще просто высыпать две кучки камешков в одно место!

Наверно, как-то так и родился алгоритм сложения! А вместе с ним зародилась и математика. Как способ повышать эффективность алгоритмов Переносом в более удобную область. И эта область только поначалу была камешками, а в последствие дополнилась числами, интегралами, исчислением предикатов и много, много, много еще чем.

Но, а как же второй близнец «Трансляция«? Да, да… он тоже нам нужен, и тоже нужен Алисе.

Математические обозначения знаки, буквы и сокращения

Для объявления надо написать название типа переменных (int, float или char и др.), а затем через запятую имена всех объявляемых этим типом переменных. При желании можно сразу записать в новую ячейку нужное число, как показано в примерах ниже. Если переменной не присваивается никакого значения, то в ней находится «мусор», то есть то, что было там раньше.

По описанию переменной в памяти компьютера резервируется ячейка для хранения ее значения. В зависимости от объявленного типа переменной ячейка может иметь разную внутреннюю структуру, т.е. содержать различное число байт.

int a; // выделить память под целую переменную a

float b, c; //две вещественных переменных b и c

int Tu104, Dl86=23, Yak42; //три целых переменных,

//причем в D186 сразу записывается число 23.

float x=4.56, y, z; //три вещественных переменных,

// причем в x сразу записывается число 4.56.

char c, c2=’A’, m; //три символьных переменных,

//причем в c2 сразу записывается символ ‘A’.

Арифметические выражения строятся из операндов, арифметических операций и круглых скобок. Операндами могут быть константы, переменные и функции.

В бесскобочных арифметических выражениях операции выполняются слева направо в соответствии с их приоритетом.

1. * (умножение); / (деление); % ( остаток от деления целых чисел).

2. + (сложение); — (вычитание).

Изменить порядок выполнения операций можно с помощьюкруглых скобок. Выражение, заключенное в круглые скобки, выполняется в первую очередь. Например, выражению: а/b*с соответствует математическая запись: , а выражению а/(b*с) – запись .

Тип арифметического выражения определяется типом входящих и него операндов.

Арифметическое выражение является целым, если все входящие и него операнды целого типа.

Если в арифметическом выражении содержится хотя бы один вещественный операнд, то результат — вещественный. Целые операнды в вещественном арифметическом выражении всегда преобразуются к вещественному типу.

Операция выделения остатка или деление по модулю ( % ) применима только к целым числам. Результат ее выполнения имеет целый тип.

Исключение составляет операция деления с использованием символа ‘/’ (косая черта). Результат выполнения этой операции всегда зависит от типа операндов.

Например, значением выражения 2/5 будет число 0.

Прямая на плоскости

Общее уравнение прямой: Ax+By+C=0.
Уравнение прямой с угловым коэффициентом: y=kx+b (k – угловой коэффициент).
Острый угол между прямыми y=k₁x+b₁ и y=k₂x+b₂ определяется по формуле:

k₁=k₂ — условие параллельности прямых y=k₁x+b₁ и y=k₂x+b_2.
Условие перпендикулярности этих же прямых:

Уравнение прямой, имеющей угловой коэффициент k, и проходящей

через точку М(х₁; у₁), имеет вид: у-у₁=k (х-х₁).

Уравнение прямой, проходящей через две данные точки (х1; у1) и (х2; у2) имеет вид:

Длина отрезка М1М2 с концами в точках М1(х1; у1) и М2(х2; у2):

Координаты точки М(хо; уо) – середины отрезка М1М2

Координаты точки С(х; у), делящей в заданном отношении λ отрезок М1М2 между точками М1(х1; у1) и М2(х2; у2):

Расстояние от точки М(хо; уо) до прямой ax+by+c=0:

ЗНАКИ МАТЕМАТИЧЕСКИЕ

ЗНАКИ МАТЕМАТИЧЕСКИЕ — условные обозначения (символы) различных математических понятий (операций, функций, отношений и др.). Для некоторых З. м. существует общепринятая символика как в нашей стране, так и за рубежом; однако все еще существует разнобой как у нас, так и за рубежом в символике одних и тех же понятий. Так, во всех европейских странах отношение длины окружности к длине диаметра, как и у нас в стране, обозначают символом (греч. буква «пи»). Логика обозначения функции, обратной синусу, не поддается строгому объяснению: в нашей стране эта функция обозначается , англичане же эту функцию обозначают (в этом есть тоже определенный резон, так как функция, обратная функции обозначается символом ).

Сумму конечного числа слагаемых обозначают знаком , а бесконечного числа слагаемых в виде (иногда встречаются обозначения и такие: и ).

О роли З. м. великий русский математик Н. И. Лобачевский писал: «Подобно тому как дар слова обогащает нас мнениями других, так язык математических знаков служит средством еще более совершенным, более точным и ясным, чтобы один передавал другому понятия, которые он приобрел, истину, которую он постигнул, и зависимость между всеми частями, которую он открыл…» (Н. И. Лобачевский. Наставление учителям математики в гимназиях).

Удачно выбранные З. м. могут содействовать развитию той или иной отрасли математических знаний; так, тензорное исчисление в XIX в. получило успешное развитие благодаря удачно созданной символике. З. м. прошли довольно длительную и сложную историю своего развития, прежде чем они приняли современный вид.

Знаки в математике в основном подразделяются на три группы:

1) знаки математических объектов;

2) знаки различных операций;

3) знаки всевозможных отношений.

Приведем несколько примеров.

1. Точки обычно обозначаются прописными буквами латинского алфавита или иногда цифрами ; прямые, проходящие через две какие-либо точки, обозначаются так: или или обозначаются строчными буквами латинского алфавита . Отрезки и обозначаются в школьном курсе математики так: , а длины этих отрезков — .

2. З. м. операций (действий): + и — (сложение и вычитание) были введены немецкими математиками в конце XV в.; З. м. • и : (умножение и деление) ввел Г. Лейбниц (1698); З. м. (степени) введены Р. Декартом (1637), З. м. (корни) введены X. Рудольфом (1525) и А. Жираром (1629); З. м. — И. Кеплером (1624), — Б. Кавальери (1632); знаки тригонометрических функций — Эйлером (1753); З. м. ! (факториал) — X. Крампом (1808); З. м. (дифференциалы и интеграл) — Г. Лейбницем (1675); в печати появились в 1684); З. м. (модуль) — Вейерштрассом (1841).

3. З. м. отношений: = (равенство) введено Ф. Рекордом (1557); (больше, меньше) — Т. Гарриотом (1631); (отношение параллельности) — У. Оутредом (1677); (знак отношения перпендикулярности) — П. Эригоном. Это все З. м. бинарных отношений. З. м. (принадлежности элемента множеству; сокращение греческого слова — быть) введен итальянским математиком и логиком Джузеппе Пеано (1858—1922).

Логические выражения и таблица истинности

Примеры задач с решениями по этой теме Пройти тестирование по теме Контрольная по теме

Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.

Логическое выражение — составные высказывания в виде формулы.

Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».

Алгоритм построения таблицы истинности:

1.подсчитать количество переменных n в логическом выражении;

2. определить число строк в таблице по формуле m=2n, где n — количество переменных;

3. подсчитать количество логических операций в формуле;

4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;

5. определить количество столбцов: число переменных + число операций;

6. выписать наборы входных переменных;

7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.

Заполнение таблицы:

1.разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;

2.разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;

3.продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.

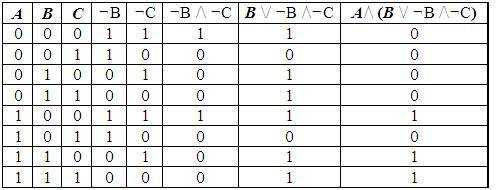
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.

Количество логических переменных 3, следовательно, количество строк — 23 = 8.

Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.

Пример 2. Определите истинность логического выражения F(А, В) = (А\/ В)/\(¬А\/¬В) .

1. В выражении две переменные А и В (n=2).

2. m_строк=2n, m=22=4 строки.

3. В формуле 5 логических операций.

4. Расставляем порядок действий

1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).

5. К_{столбцов}=n+5=2+5=7 столбцов.

А	В	А\/ В	¬А	¬В	¬А\/¬В	F
1	1	1
1	1	1	1	1
1	1	1	1	1
1	1	1

Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.

Пример 3. Построёте таблицу истинности для логического выражения

F = (A\/ B) /\ ¬С

В данной функции три логические переменные – А, В, С
количество строк таблицы = 23 =8
В формуле 3 логические операции.
Расставляем порядок действий

1) А\/ В; 2) ¬С; 3) (AVB) /\ ¬С .

количество столбцов таблицы = 3 + 3 = 6

А	В	С	A\/B	¬С	(A\/B) /\ ¬С
1
1
1	1	1	1
1	1	1
1	1	1	1
1	1	1
1	1	1	1	1
1	1	1	1

Пример 4. Определите истинность формулы: F = ((С \/В) => В) /\ (А /\ В) => В.

Построим таблицу истинности этой формулы.

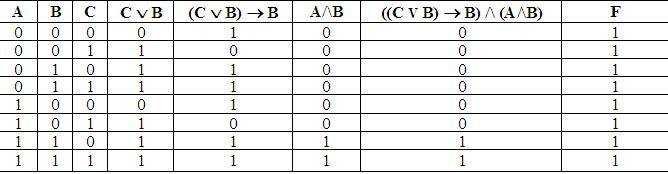
Ответ: формула является тождественно истинной.

Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.

Дан фрагмент таблицы истинности выражения F:

X	Y	Z	F
1
1
1	1

Какое выражение соответствует F?

1) ¬X/\¬Y/\Z 2) ¬X\/¬Y\/Z 3) X\/Y\/¬Z 4) X\/Y\/Z

Решение (вариант 1, через таблицы истинности):

Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:

X	Y	Z	F	¬X	¬Y	¬Z	¬X/\¬Y/\Z	¬X\/¬Y\/Z	X\/Y\/¬Z	X\/Y\/Z
1	1	1	1	1	1
1	1	1	1	1	1
1	1	1	1	1	1	1

Очевидно, что значения заданной функции F совпадают со значениями выражения X\/Y\/¬Z. Следовательно, правильный ответ – 3.

Ответ: 3

Решение (Вариант 2):

Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.

Рассмотрим данный конкретный пример:

1)первое заданное выражение ¬X/\¬Y/\Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;

2)второе заданное выражение ¬X\/¬Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы;

3)третье выражение X\/Y\/¬Z соответствует F при всех предложенных комбинациях X,Y и Z;

4)четвертое выражение X\/Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.

Ответ: 3

О происхождения знака

Появление символа связано с греческими языком, но сама буква появилась от стародревнего финийского языка, в котором именовалась – далет, что обозначало («вход в дверь»). Выглядела «далет» как перевернутый влево равнобедренный треугольник. В греческом алфавите, была такая буква. Позже эта буква дала начало всем известной буквы латинского набора – D , которая и поныне есть во многих алфавитных рядах разных государств мира, к примеру, английский алфавит ее содержит.

Буква, которая служит аналогом в русском алфавите – Д, а вот символ везде одинаков и изображается, как геометрическая фигура, а именно треугольник с равными сторонами (Δ). Эта версия является заглавной, прописная версия выглядит немного иначе, представляя собой кружок с хвостиком, похожий на обозначение в физике плотности (δ).

Что означает знак в алгебре?

Алгебра — это раздел математики, который изучает структуры и операции над ними, такие как числа, переменные, функции и т.д. Знаки в алгебре являются символами, используемыми для обозначения этих операций и структур.

Один из наиболее распространенных знаков в алгебре — это ‘+’ (плюс). Он обозначает операцию сложения. Например, если мы имеем два числа: 3 и 5, то их суммой будет 3+5=8.

Еще один знак — ‘-‘ (минус), обозначает операцию вычитания. Если мы вычитаем 5 из 7, то мы пишем это как 7-5=2.

Другой знак — ‘*’ (звездочка), используется для обозначения умножения. Например, если мы имеем два числа: 2 и 4, то их произведение будет 2*4=8.

‘/’ (деление) — это знак для обозначения операции деления. Например, если мы делим 6 на 2, то мы пишем это как 6/2=3.

Знак ‘^’ (возведение в степень) используется для обозначения возведения в степень. Например, если мы возводим число 2 в квадрат, то это будет 2^2=4.

Еще один знак в алгебре — ‘=’ (равно) — используется для обозначения равенства. Например, если мы пишем уравнение 2+x=6, то мы можем решить его, написав x=4.

В алгебре есть и более сложные знаки, такие как скобки, индексы и дроби. Знание значений этих знаков является важным для успешного изучения алгебры и решения математических проблем.

Параллельность. У.Оутред (посмертное издание 1677 года).

Параллельность – отношение между некоторыми геометрическими фигурами; например, прямыми. Определяется по-разному в зависимости от различных геометрий; например, в геометрии Евклида и в геометрии Лобачевского. Знак параллельности известен с античных времён, его использовали Герон и Папп Александрийский. Сначала символ был похож на нынешний знак равенства (только более протяжённый), но с появлением последнего, во избежание путаницы, символ был повёрнут вертикально ||. В таком виде он появился впервые в посмертном издании работ английского математика Уильяма Оутреда в 1677 году.

Равенство. Р.Рекорд (1557).

Знак равенства предложил уэльский врач и математик Роберт Рекорд в 1557 году; начертание символа было намного длиннее нынешнего, так как имитировало изображение двух параллельных отрезков. Автор пояснил, что нет в мире ничего более равного, чем два параллельных отрезка одинаковой длины. До этого в античной и средневековой математике равенство обозначалось словесно (например est egale). Рене Декарт в XVII веке при записи стал использовать æ (от лат. aequalis), а современный знак равенства он использовал чтобы указать, что коэффициент может быть отрицательным. Франсуа Виет знаком равенства обозначал вычитание. Символ Рекорда получил распространение далеко не сразу. Распространению символа Рекорда мешало то обстоятельство, что с античных времён такой же символ использовался для обозначения параллельности прямых; в конце концов было решено символ параллельности сделать вертикальным. В континентальной Европе знак «=» был введён Готфридом Лейбницем только на рубеже XVII–XVIII веков, то есть более чем через 100 лет, после смерти впервые использовавшего его для этого Роберта Рекорда.

Корни. К.Рудольф (1525), Р.Декарт (1637), А.Жирар (1629).

Арифметический корень n-й степени из действительного числа а≥0, – неотрицательное число n-я степень которого равна а. Арифметический корень 2-й степени называется квадратным корнем и может записываться без указания степени: √. Арифметический корень 3-й степени называется кубическим корнем. Средневековые математики (например, Кардано) обозначали квадратный корень символом R_x (от латинского Radix, корень). Современное обозначение впервые употребил немецкий математик Кристоф Рудольф, из школы коссистов, в 1525 году. Происходит этот символ от стилизованной первой буквы того же слова radix. Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт (1637) для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня. Кубический корень в XVI веке обозначался следующим образом: R_x.u.cu (от лат. Radix universalis cubica). Привычное нам обозначение корня произвольной степени начал использовать Альбер Жирар (1629). Закрепился этот формат благодаря Исааку Ньютону и Готфриду Лейбницу.

Сравнимость. К.Гаусс (1801).

Сравнение – соотношение между двумя целыми числами n и m, означающее, что разность n–m этих чисел делится на заданное целое число а, называемое модулем сравнения; пишется: n≡m(mod а) и читается «числа n и m сравнимы по модулю а». Например, 3≡11(mod 4), так как 3–11 делится на 4; числа 3 и 11 сравнимы по модулю 4. Сравнения обладают многими свойствами, аналогичными свойствам равенств. Так, слагаемое, находящееся в одной части сравнения можно перенести с обратным знаком в другую часть, а сравнения с одним и тем же модулем можно складывать, вычитать, умножать, обе части сравнения можно умножать на одно и то же число и др. Например,

3≡9+2(mod 4) и 3–2≡9(mod 4)

– одновременно верные сравнения. А из пары верных сравнений 3≡11(mod 4) и 1≡5(mod 4) следует верность следующих:

3+1≡11+5(mod 4)

3–1≡11–5(mod 4)

3·1≡11·5(mod 4)

32≡112(mod 4)

3·23≡11·23(mod 4)

В теории чисел рассматриваются методы решения различных сравнений, т.е. методы отыскания целых чисел, удовлетворяющих сравнениям того или иного вида. Cравнения по модулю впервые использовались немецким математиком Карлом Гауссом в его книге «Арифметические исследования» 1801 года. Он же предложил утвердившуюся в математике символику для сравнений.