Родоначальник античной науки фалес милетский и его теоремы

Пример задачи

Дан отрезок AB на плоскости. Разделите его на 3 равные части.

Решение

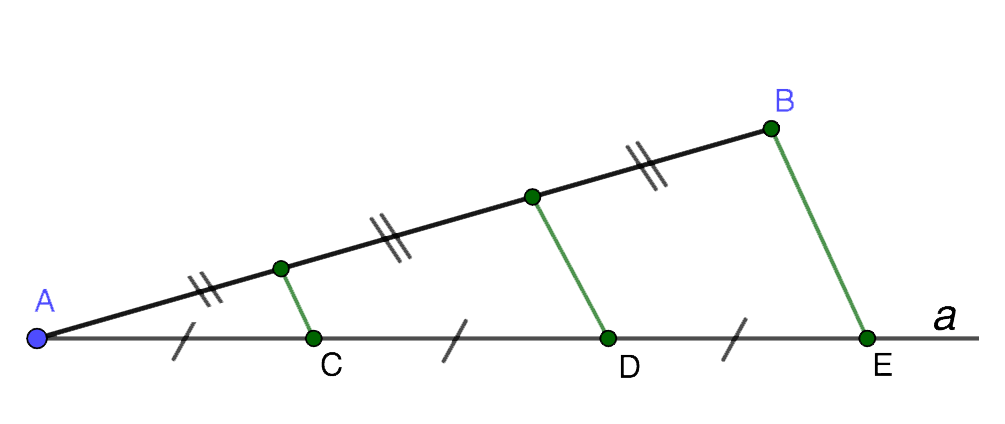
Проведем из точки A прямую a и отметим на ней три подряд идущих равных отрезка: AC, CD и DE.

Крайнюю точку E на прямой a соединяем с точкой B на отрезке. После этого через оставшиеся точки C и D параллельно BE проведем две прямые, пересекающие отрезок AB.

Образованные таким образом точки пересечения на отрезке AB делят его на три части, равные между собой (согласно теореме Фалеса).

Публикации по теме:

• Нахождение площади квадрата: формула и примеры Нахождение площади прямоугольника: формула и пример Нахождение площади треугольника: формула и примеры Нахождение площади круга: формула и примеры Нахождение площади ромба: формула и примеры Нахождение площади параллелограмма: формула и примеры Нахождение площади эллипса: формула и пример Нахождение площади выпуклого четырехугольника: формула и пример Нахождение периметра квадрата: формула и задачи Нахождение периметра треугольника: формула и задачи Нахождение периметра прямоугольника: формула и задачи Нахождение периметра трапеции: формула и задачи Нахождение периметра параллелограмма: формула и задачи Нахождение длины окружности: формула и задачи Теорема Пифагора для прямоугольного треугольника: формула и задачи Теорема косинусов для треугольника: формула и задачи Теорема синусов для треугольника: формула и задачи Теорема о сумме углов треугольника: формула и задачи Тригонометрические функции острого угла в прямоугольном треугольнике Нахождение объема конуса: формула и задачи Нахождение объема цилиндра: формула и задачи Нахождение объема куба: формула и задачи Нахождение объема пирамиды: формула и задачи Нахождение площади правильного шестиугольника: формула и примеры Нахождение объема тетраэдра: формула и задачи Нахождение объема призмы: формула и задачи Нахождение объема параллелепипеда: формула и задачи Нахождение площади поверхности куба: формула и задачи Нахождение площади поверхности цилиндра: формула и задачи Нахождение площади поверхности конуса: формула и задачи Нахождение площади поверхности шара (сферы): формула и задачи Нахождение площади поверхности вписанного в цилиндр шара Нахождение радиуса круга: формула и примеры Нахождение радиуса цилиндра: формула и примеры Нахождение площади прямоугольного параллелепипеда: формула и пример Нахождение площади правильной призмы: формула и задачи Нахождение площади правильной пирамиды: формулы Формула Герона для треугольника Теорема о внешнем угле треугольника: формулировка и задачи Теорема Чевы: формулировка и пример с решением Теорема Стюарта: формулировка и пример с решением Теорема о трех перпендикулярах Геометрическая фигура: треугольник Признаки равенства треугольников Признаки подобия треугольников Признаки равенства прямоугольных треугольников Свойства прямоугольного треугольника Свойства равнобедренного треугольника: теория и задача Определение и свойства медианы треугольника Определение и свойства медианы прямоугольного треугольника

Дан отрезок AB на плоскости. Разделите его на 3 равные части.

Теорема Фалеса: формулировка и пример решения задачи

В данной публикации мы рассмотрим одну из основных теорем по геометрии 8 класса – теорему Фалеса, которая получила такое название в честь греческого математика и философа Фалеса Милетского. Также разберем пример решения задачи для закрепления изложенного материала.

скрыть

геометрия — почему основная теорема о пропорциональности всегда верна?

спросил 6 лет, 8 месяцев назад

Изменено
3 года, 9 месяцев назад

Просмотрено
1к раз

$\begingroup$

Выписка:

Теперь есть несколько способов доказать это, а также доказать обратное. Следовательно, мы можем убедить себя, что это действительно так. Но почему? Что такого в природе, что делает это «истинным»?

Если представить два объекта, равномерно движущихся из точки $A$ по линиям $AB$ и $AC$ с разными скоростями, то $x$ и $y$. Вы берете несколько перехватов времени $t_1, t_2, t_3 и т. д. $. Скажем так, точки, которые они делают, помечены так же, как $A_{xt_1}, A_{xt_2} и т. д.$ и $B_{yt_1}, B_{yt_2} и т. д. $… Вы всегда замечали, что $$ A_{xt_1}B_{yt_1} \параллельно A_{xt_2}B_{yt_2} \параллельно A_{xt_3}B_{yt_3} …$$
Я зашел в тупик с этим вопросом: почему так?!

геометрия

$\endgroup$

2

$\begingroup$

Во многих языках это известно как Теорема Фалеса.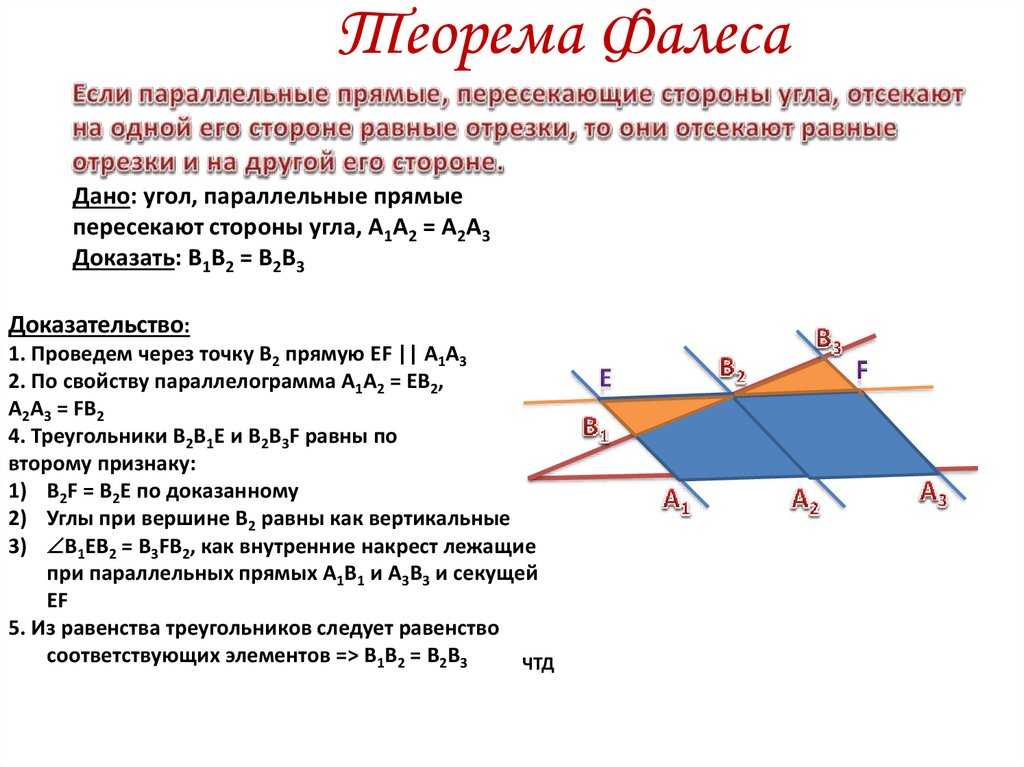

Позвольте мне сначала сказать, что я не согласен с комментариями, что это доказывается с использованием подобных треугольников. Вместо этого для доказательства фактов о подобных треугольниках обычно используется теорема Фалеса.

На странице английской Википедии приведено доказательство теоремы с использованием площади. Но поскольку площадь представляет собой сложное понятие, возможно, предпочтительнее привести доказательство, в котором площадь не используется.

Теорема обычно доказывается в следующие шаги:

1. Пусть несколько параллельных прямых пересекают две прямые $l_1$ и $l_2$, секущие к ним. Если параллельные прямые отмечают равные отрезки на $l_1$, то они также отмечают равные отрезки на $l_2$. Доказательство этого шага использует факты о параллелограммах и критерии конгруэнтности треугольников.

2. Даны три параллельные прямые, пересекающие две прямые $l_1$ и $l_2$, предположим, что они отмечают на $l_1$ отрезки, находящиеся в некотором рациональном соотношении.

   Тогда отрезки, отмеченные на $l_2$, находятся в таком же отношении. Это доказывается вставкой дополнительных параллельных линий так, чтобы все линии были на равном расстоянии друг от друга.

3. Пункт 2 распространен на иррациональные отношения. Делается это абсурдно: предположим, что отношения на $l_1$ и $l_2$ различны. Тогда должно быть какое-то рациональное отношение, которое больше одного и меньше другого. (Любые два различных действительных числа имеют между собой некоторое рациональное число. Геометрически это соответствует использованию аксиомы Архимеда.) Затем вы используете пункт 2, чтобы получить противоречие.

К сожалению, я не знаю книги на английском языке, где проводится это доказательство. Но доказательство можно найти в Geometría elemental Погорелова (испанский перевод с русского). Кажется вероятным, что доказательство может быть также дано в книге Киселева по геометрии, которая недавно была переведена на английский язык, но я не знаю наверняка.

$\endgroup$

$\begingroup$

Основная идея в том, что
два треугольника подобны,
потому что их соответствующие углы
подобные.

Отсюда
(который,
конечно,
суть доказательства)
соответствующие стороны
пропорциональны.

Иногда
полагая, что теорема верна
просто сводится к пониманию доказательства.

$\endgroup$

1

$\begingroup$

После долгих размышлений это можно доказать с помощью других истин. Например, для закона синусов, т. е.

$$\frac{a}{\sin{A}} = \frac{b}{\sin{B}}= \frac{c}{\sin{C}} $$

Это легко доказать. Нужно понимать, что синус также является отношением. (Плюс, если вы понимаете, как формируется это отношение. Вы можете легко понять это из доказательства).

Но суть этого закона в том, что

$$\frac{\text{длина стороны}}{\text{отношение (длины высоты) от другой вершины к (длине соответствующей соседней стороны )}} = \text{constant}$$

Член в знаменателе зависит от направления стягиваемого угла.

Параллельные линии просто дают еще один способ выразить соотношение синусов. Следовательно, подключив это к результату закона синусоиды, мы получим желаемое соотношение.

Вот почему… или я так думаю.

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Теорема Фалеса

Одна из основополагающих теорем (теорема Фалеса) в геометрии говорит о том, что проведенные через концы одинаковых отрезков прямой параллельные линии отсекают на  другой прямой тоже одинаковые по длине отрезки.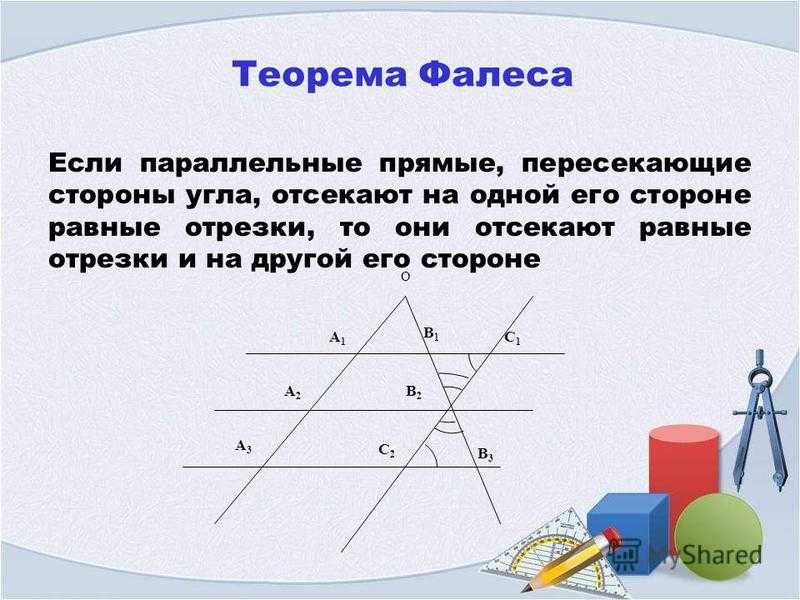

формулировка теоремы Фалеса

Ключевые слова в теореме (при любой формулировке) — прямые, отрезки, равные, пропорциональные, параллельные. Это говорит о том, что теорема Фалеса касается только планиметрии, то есть изображения линий на плоскости. Она очень важна для картографии и навигации, широко используется в архитектуре и живописи, строительстве и проектировании.

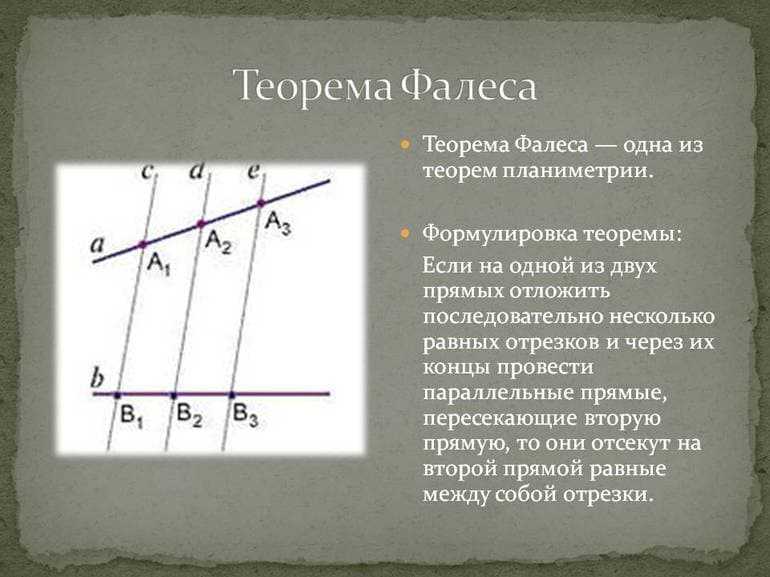
Классической формулировки, единой в своем роде нет. Например, формулировку можно услышать  в такой редакции:

Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.

А можно и в такой:

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Рис 2.

Если внимательно присмотреться, то можно увидеть, что одно утверждение не противоречит другому, а рисунки практически идентичны. Если продолжить прямые на первом рисунке по получим тот же угол.

Кроме прямых, которые проходят под углом, такая же картина происходит при пересечении параллельных прямых. Разница состоит в том, что на пересекающихся прямых отрезки АВ и А₁В₁  могут быть как одинаковыми, так и пропорциональными, в зависимости от угла наклона секущих. А для случая параллельных — только одинаковыми. Если обобщить два случая, то обобщенная теорема Фалеса звучит так: Параллельные прямые отсекают на секущих пропорциональные отрезки.

A₁A₂/B₁B₂=A₂A₃/B₂B₃=A₁A₃/B₁B₃

Для иллюстрации можно воспользоваться рисунком 1.

Теорема Фалеса это не только теоретическое утверждение, доказанное методами математики, но и практический инструмент для построения различных фигур.

Для решения задачи нарисуем отрезок ВС, образующий с данным  ВА угол. Как видим, отрезок ВС проходит вдоль клеток на бумаге, что позволяет выбрать на нем равные отрезки. В нашем случае, это:

BD=DE=EF=FG=GH=HJ=JC.

Начиная от крайних точек А и С проведем параллельные линии, пересекающие отрезок ВА. На нем тоже получиться семь равных отрезков: BR=RP=PN=NM=ML=LK=KA.

С таким же успехом мы можем разделить отрезок на 5, 6, 4 или любое другое количество равных частей. Суть метода состоит в том, что длину отрезка ВС мы заведомо выбираем такой, чтобы его можно было легко разделить на заданное количество частей. Например, длина отрезка ВА 37 см, а его нужно разделить на 5 частей. Выбираем длину отрезка ВС в 25 см, отмечаем точки и выполняем построение по теореме Фалеса.

Не менее широко используется и теорема, названная обратной. То есть, доказательства требует не равность или пропорциональность отрезков, а параллельность прямых.

обратная теорема Фалеса

Если две или более прямых (a, b, c) отсекают от двух других прямых (d, f) равные или пропорциональные отрезки, то они параллельные.

Утверждение справедливо, независимо от того, параллельные d, f или пересекаются.

Математика, тем более, геометрия, наука точная. Каждое утверждение, кроме аксиом, требует доказательства. В геометрии под термином «теорема» подразумевается утверждение, которое доказано на базе ранее полученных знаний в виде аксиом и других теорем.

Теорема Фалеса с доказательством приведена в большинстве учебников. В отличие от теоремы Пифагора, доказательств у нее меньше, но все они четкие, понятные и аргументированные. Покажем одно из них.

Не будем повторять формулировок, продемонстрируем только ход мыслей и выполним необходимые построения:

Выберем точку В₂  и проведем прямую, параллельную стороне угла ОС.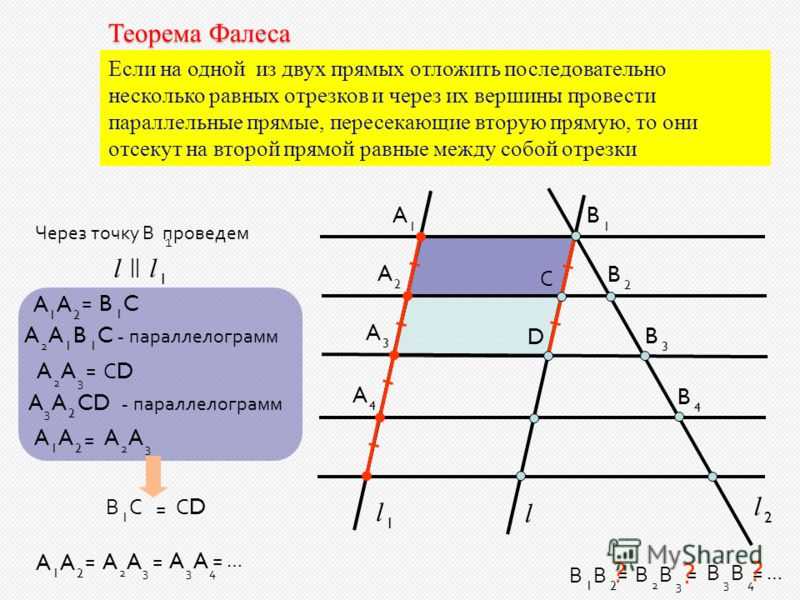

₁₃

А₁FЕА₃ замечаем, что А₁F и ЕА₃ параллельны по определению, а А₁А₃ и FВ₃ параллельны по построению. Отсюда вытекает, что А₁ FЕА ₃ — параллелограм и А₁А₃ = EF.

Аналогичным образом доказываем равенство других сторон и получаем, что по равенству вертикальных и внутренних углов ∠B₁B₂F=∠B₃B₂E  и ∠B₂FB₁=∠B₂EB₃ треугольники B₂B₁F и B₂B₃E равны, откуда вытекает, что B₁B₂=B₂B₃.

Именно это и требовалось доказать.

По легенде, впервые на практике использовал теорему греческий философ Фалес Милетский. Он применил ее для измерения высоты пирамиды Хеопса, пользуясь падающей на песок тенью. Для  сравнения длины отрезков использовалась воткнутая рядом палка.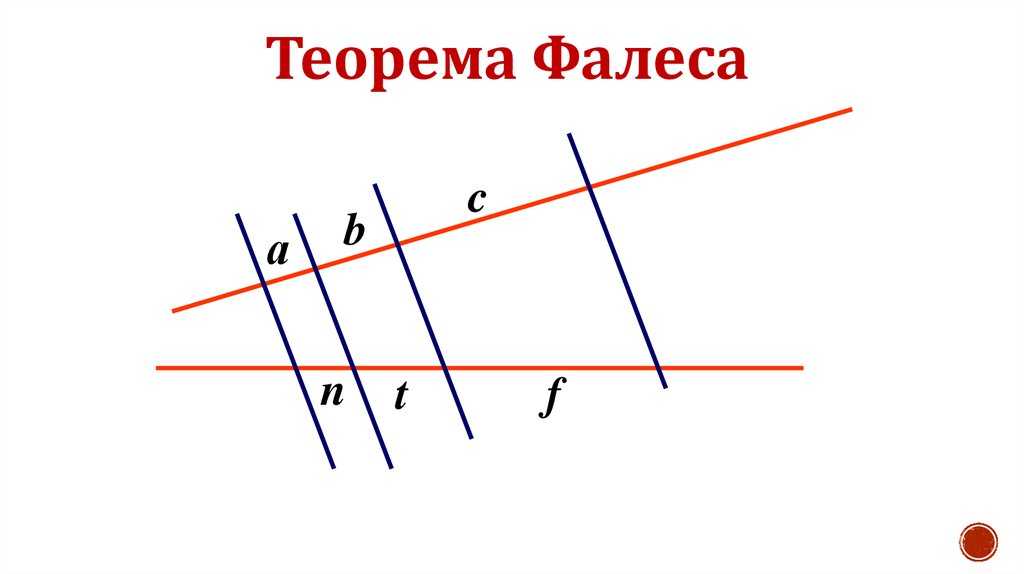

Но доказательство теоремы, самое давнее из известных, зафиксированных в письменных источниках, дано в книге «Элементы» другого философа и математика — Эвклида. Тем не менее, утверждение получило имя Фалеса, под которым известно до сих пор.

Математика

Четыре отрезка называются пропорциональными, если они такой величины, что образуют пропорцию. В этом случае отношение двух отрезков по длине равно отношению других двух отрезков.

Так четыре отрезка AB, CD, EF, GH (черт. 144) будут пропорциональными, если они удовлетворяют пропорции:

В этой пропорции под отрезками AB, CD подразумевают их длины. Так как длина отрезков может быть выражена числом, которое выражает отношение длины отрезка к длине, принятой за единицу, то под отрезками AB, CD, EF, GH можно подразумевать и сами числа.

На этом основании пропорция из отрезков обладает всеми свойствами пропорции, составленной из чисел.

Члены пропорции можно переставлять, перемножать и т. д.

Таким образом из пропорции (1) вытекает равенство

а также пропорции:

AB/EF = CD/GH, GH/CD = EF/AB и т. д.

Каждый из отрезков по отношению к остальным называется четвертым пропорциональным .

Таким образом отрезок GH будет четвертым пропорциональным отрезкам EF, CD, AB. Отрезок AB четвертым пропорциональным отрезкам CD, EF, GH.

Отрывок, характеризующий Теорема Фалеса

Анатоль последнее время переселился к Долохову. План похищения Ростовой уже несколько дней был обдуман и приготовлен Долоховым, и в тот день, когда Соня, подслушав у двери Наташу, решилась оберегать ее, план этот должен был быть приведен в исполнение. Наташа в десять часов вечера обещала выйти к Курагину на заднее крыльцо. Курагин должен был посадить ее в приготовленную тройку и везти за 60 верст от Москвы в село Каменку, где был приготовлен расстриженный поп, который должен был обвенчать их. В Каменке и была готова подстава, которая должна была вывезти их на Варшавскую дорогу и там на почтовых они должны были скакать за границу.
У Анатоля были и паспорт, и подорожная, и десять тысяч денег, взятые у сестры, и десять тысяч, занятые через посредство Долохова.
Два свидетеля – Хвостиков, бывший приказный, которого употреблял для игры Долохов и Макарин, отставной гусар, добродушный и слабый человек, питавший беспредельную любовь к Курагину – сидели в первой комнате за чаем.
В большом кабинете Долохова, убранном от стен до потолка персидскими коврами, медвежьими шкурами и оружием, сидел Долохов в дорожном бешмете и сапогах перед раскрытым бюро, на котором лежали счеты и пачки денег. Анатоль в расстегнутом мундире ходил из той комнаты, где сидели свидетели, через кабинет в заднюю комнату, где его лакей француз с другими укладывал последние вещи. Долохов считал деньги и записывал.
– Ну, – сказал он, – Хвостикову надо дать две тысячи.
– Ну и дай, – сказал Анатоль.
– Макарка (они так звали Макарина), этот бескорыстно за тебя в огонь и в воду. Ну вот и кончены счеты, – сказал Долохов, показывая ему записку. – Так?
– Да, разумеется, так, – сказал Анатоль, видимо не слушавший Долохова и с улыбкой, не сходившей у него с лица, смотревший вперед себя.

Доказательство теоремы Фалеса

Математика, тем более, геометрия, наука точная. Каждое утверждение, кроме аксиом, требует доказательства. В геометрии под термином «теорема» подразумевается утверждение, которое доказано на базе ранее полученных знаний в виде аксиом и других теорем.

Теорема Фалеса с доказательством приведена в большинстве учебников. В отличие от теоремы Пифагора, доказательств у нее меньше, но все они четкие, понятные и аргументированные. Покажем одно из них.

Не будем повторять формулировок, продемонстрируем только ход мыслей и выполним необходимые построения:

Выберем точку В₂ и проведем прямую, параллельную стороне угла ОС. При этом отмечаем, что А₁А₃ || EF. Рассматривая четырехугольник

А₁FЕА₃ замечаем, что А₁F и ЕА₃ параллельны по определению, а А₁А₃ и FВ₃ параллельны по построению. Отсюда вытекает, что А₁ FЕА ₃ — параллелограм и А₁А₃ = EF.

Аналогичным образом доказываем равенство других сторон и получаем, что по равенству вертикальных и внутренних углов ∠B₁B₂F=∠B₃B₂E и ∠B₂FB₁=∠B₂EB₃ треугольники B₂B₁F и B₂B₃E равны, откуда вытекает, что B₁B₂=B₂B₃.

Именно это и требовалось доказать.

Доказательство теоремы Фалеса

Докажем эту теорему.

Рассмотрим рисунок:

теоремы Фалеса. Автор24 — интернет-биржа студенческих работ» />Рисунок 3. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ

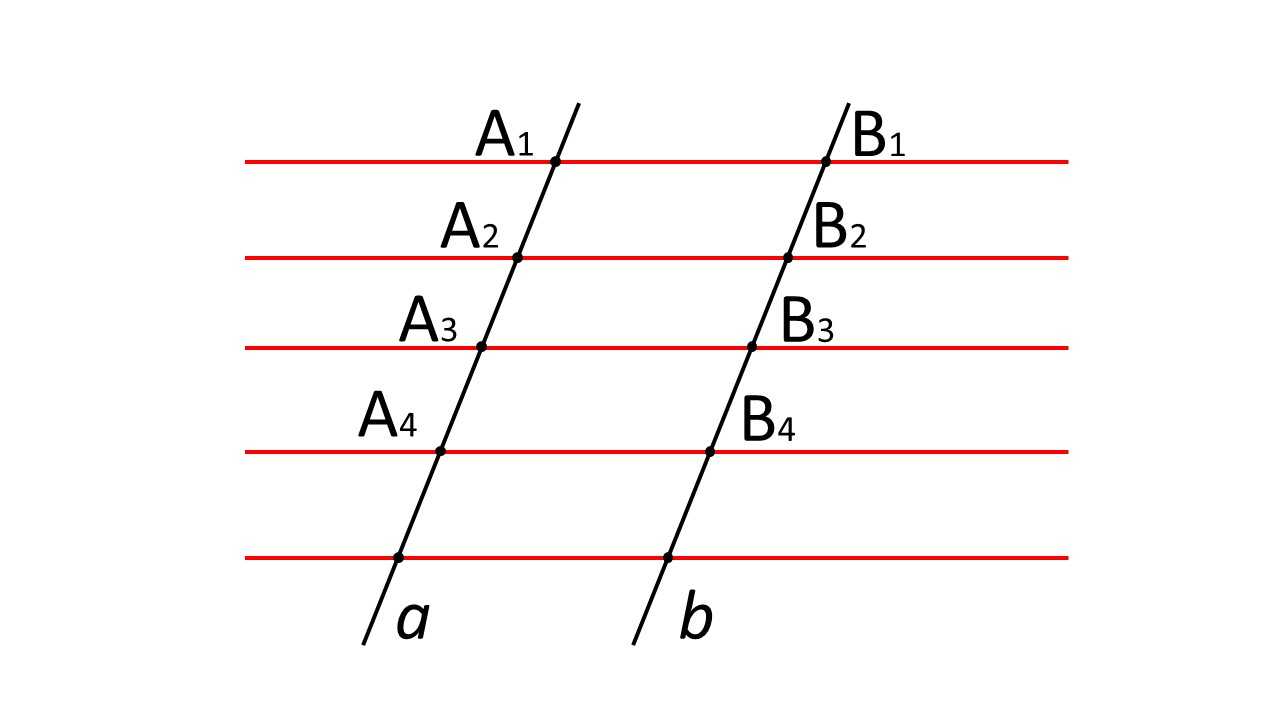
На прямой $a$ отложены следующие отрезки: $A_1 A_2, A_2 A_3, A_3 A_4,…$. Через эти отрезки проведены несколько параллельных прямых, пересекающих прямую $b$ в соответствующих точках $B_1,B_2,B_3,B_4,…$. Докажем, что отрезки $B_1 B_2, B_2 B_3, B_3 B_4,…$ равны между собой. Для начала упростим задачу и докажем следующее: $B_1 B_2 = B_2 B_3$.

На рисунке прямые $a$ и $b$ параллельны. Следовательно, $A_1 B_1 B_2 A_2$ и $A_2 B_2 B_3 A_3$ — параллелограммы. Это означает, что противоположные стороны параллелограммов равны, следовательно, $A_1 A_2 = B_1 B_2, A_2 A_3 = B_2 B_3$. И из $A_1 A_2=A_2 A_3$ следует, что $B_1 B_2= B_2 B_3$.

Есть и другой случай, когда прямые $a$ и $b$ не параллельны:

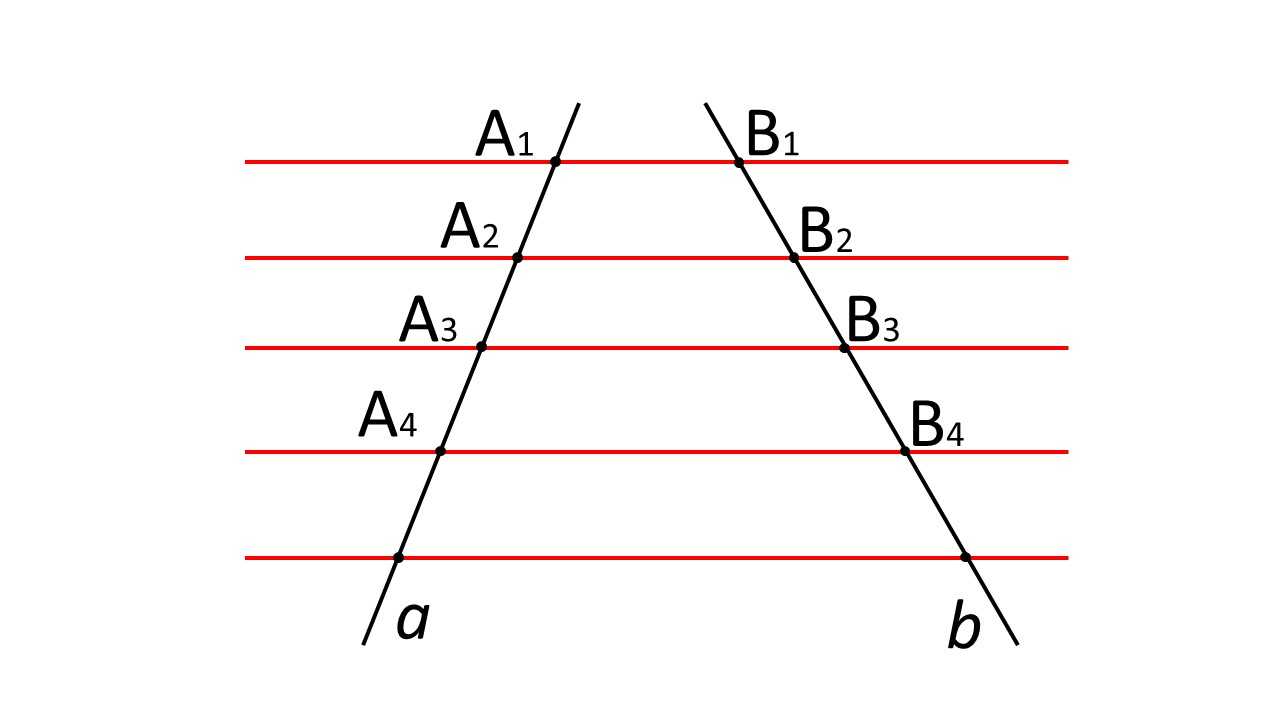Рисунок 4. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ

Проведём такую прямую $c$, которая параллельна $a$:

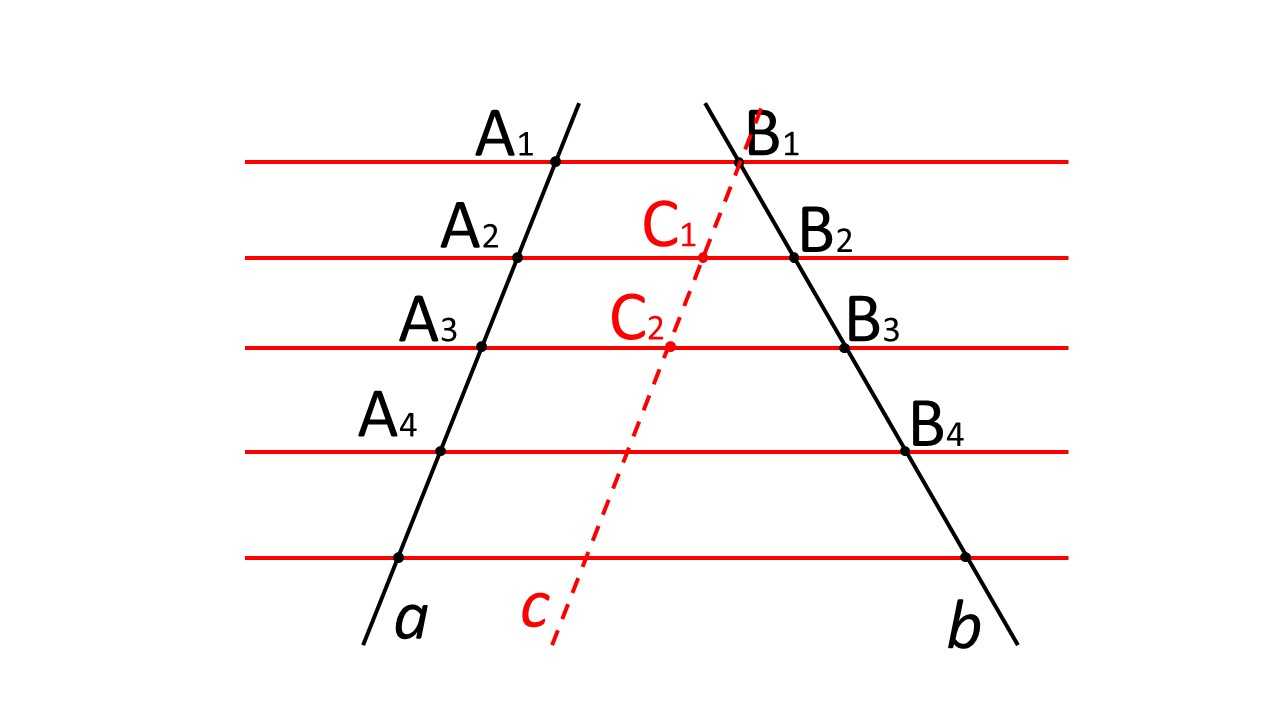Рисунок 5. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ

Прямая $c$ пересекает $A_2 B_2$ и $A_3 B_3$ соответственно в т. $C_1, C_2$. Так как $A_1 A_2=A_2 A_3$, то, по аналогии в предыдущем случае, $B_1 C_1 = C_1 C_2$.

Рассмотрим $\triangle C_2 B_1 B_3$. $C_1$ — середина $B_1 C_2$. $B_2 C_1$ параллельна $B_3 C_2$.

Проведём через точку $B_3$ такую прямую, которая параллельна $B_1 C_2$.

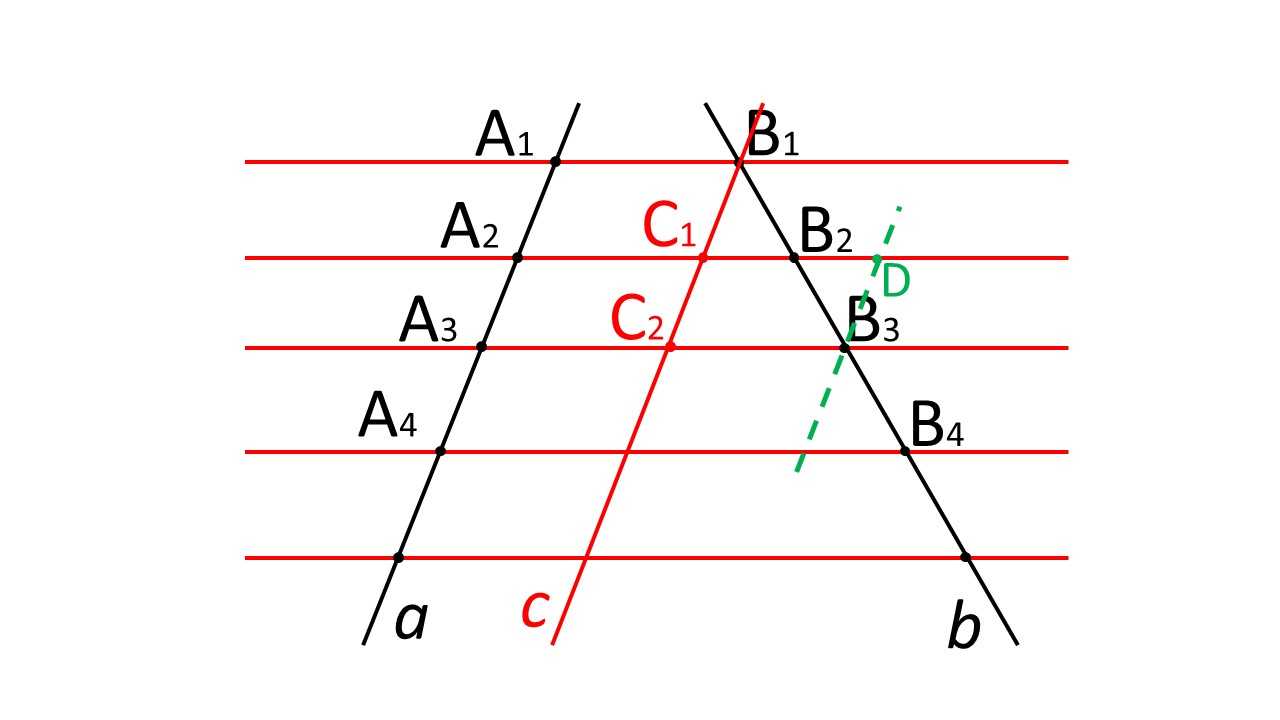Рисунок 6. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ

Точкой $D$ обозначено пересечение $B_2 C_1$ с проведённой прямой. Получаем параллелограмм $C_1 C_2 B_3 D$. Так как $C_1$ — середина $B_1 C_2$, а $C_1 C_2= B_3 D$ (как противоположные стороны параллелограмма), следовательно, $C_1 B_1 = B_3 D$.

Рассмотрим $\triangle C_1 B_1 B_2$ и $\triangle B_2 B_3 D$ Они равны согласно второму признаку равенства треугольников. То есть так как выполняются равенства $C_1 B_1 = B_3 D$, $\angle C_1 B_1 B_2 = \angle B_2 B_3 D$ и $\angle B_1 C_1 B_2=\angle B_2 D B_3$ (как лежащие накрест углы при пересечении параллельных прямых $B_1 C_2$ и $B_3 D$ секущими $B_1 B_3$ и $C_1 D$).

Следовательно, $B_1 B_2= B_2 B_3$.

Аналогично доказывается равенство $B_2 B_3=B_3 B_4$ и другие.

Таким образом, в данной статье мы полностью разобрали теорему Фалеса, произвели подробное её доказательство, фигурируя известными понятиями.

Как пользоваться теоремой Фалеса на практике

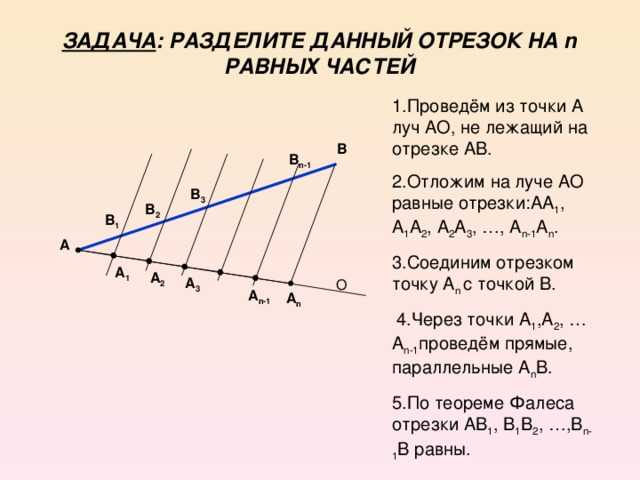
Теорема Фалеса это не только теоретическое утверждение, доказанное методами математики, но и практический инструмент для построения различных фигур. Простейшая задача — разделить на равные части произвольный отрезок ВА. Пусть этих частей будет 7.

Для решения задачи нарисуем отрезок ВС, образующий с данным  ВА угол. Как видим, отрезок ВС проходит вдоль клеток на бумаге, что позволяет выбрать на нем равные отрезки. В нашем случае, это:

BD=DE=EF=FG=GH=HJ=JC.

Начиная от крайних точек А и С проведем параллельные линии, пересекающие отрезок ВА. На нем тоже получиться семь равных отрезков: BR=RP=PN=NM=ML=LK=KA.

С таким же успехом мы можем разделить отрезок на 5, 6, 4 или любое другое количество равных частей. Суть метода состоит в том, что длину отрезка ВС мы заведомо выбираем такой, чтобы его можно было легко разделить на заданное количество частей. Например, длина отрезка ВА 37 см, а его нужно разделить на 5 частей. Выбираем длину отрезка ВС в 25 см, отмечаем точки и выполняем построение по теореме Фалеса.

Основные понятия

Фалесом было доказано, что две прямые линии RF и NS называются параллельными исключительно в том случае, если они проложены в одной плоскости и не пересекаются между собой вне зависимости от длины. Это правило всегда обозначают как RF || NS.

Абсолютно все существующие точки конкретной прямой располагаются на неизменном расстоянии от второй линии. А это значит, что все линии, которые параллельны одной прямой, являются параллельными между собой. Математики полагают, что итоговый угол между параллельными линиями приравнивается 0. Но это утверждение актуально только в том случае, если у отрезков одинаковые направления и они расположены под углом 180 градусов.

В качестве наглядного примера можно рассмотреть ситуацию, когда перпендикуляры RF, NS, EF относятся к одной и той же прямой РЕ и параллельны между собой. При этом прямая РЕ перпендикулярна ко всем остальным линиям. Итоговая длина сформированного отрезка перпендикуляра, расположенного между двумя параллельными прямыми, соответствует расстоянию средних линий. При изучении пространственной теоремы обязательно нужно понимать, что сразу восемь углов возникает при пересечении двух параллельных прямых третьей прямойю

Представленная специалистами формулировка теоремы Фалеса содержит много нюансов, в которых обязательно должен разбираться каждый человек, планирующий решать различные математические задачи. В противном случае будет сложно избежать самых распространённых ошибок. Даже кратко изложенная теория позволяет разобраться в главных математических тонкостях. Чтобы ученику стало понятно то, как именно нужно использовать теорему, можно задействовать специальные таблицы, которые помогут расширить итоговые математические возможности.

Примеры решения задач

Задание. Разделить данный отрезок на четыре равные части.

Решение. Пусть $AB$ — заданный отрезок (рис. 3), который необходимо разделить на четыре равные части.

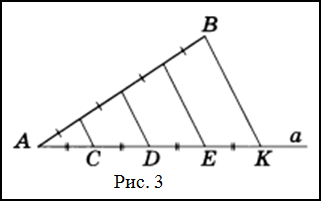
Через точку $A$ проведем произвольную полупрямую $a$ и отложим на ней последовательно четыре равных между собой отрезка $AC, CD, DE, EK$ .

Соединим точки $B$ и $K$ отрезком и проведем через оставшиеся точки $C$, $D$ и $E$ прямые, параллельные прямой $BK$ так, чтобы они пересекли отрезок $AB$ .

Согласно теореме Фалеса отрезок $AB$ разделится на четыре равные части.

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Задание. На стороне $AB$ треугольника $ABC$ отмечена точка $K$. Отрезок $CK$ пересекает медиану $AM$ треугольника в точке $P$, причем $AK = AP$. Найти отношение $BK : PM$ .

Решение. Проведем через точку $M$ прямую, параллельную $CK$, которая пересечет $AB$ в точке $D$ (рис. 4).

По теореме Фалеса $BD = KD$ .

По теореме о пропорциональных отрезках имеем, что

$P M=K D=\frac \Rightarrow B K: P M=2: 1$

Ответ. $B K: P M=2: 1$

Теорема Фалеса является частным случаем Теоремы о пропорциональных отрезках*: параллельные прямые отсекают на секущих пропорциональные отрезки.

Публикации по теме:

Свойства прямоугольного треугольника.

11.09.2019 4:13:30

2019-09-11 04:13:30

Любые данныеЛюбые данныеЛюбые данныеЛюбые данные Любые данные

Список использованных источников

1. Энциклопедия для детей. Т.11. Математика/Глав.ред.М.Д.Аксенова.-м.:Аванта+,2001.
   
2. «Единый государственный экзамен 2006. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Рособрнадзор, ИСОП – М.: Интеллект-Центр, 2006»
   
3. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина «Геометрия, 7 – 9: учебник для общеобразовательных учреждений»
   

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Доказательство. Пусть А 1 , А 2 , А 3 — точки пересечения параллельных прямых с одной из сторон угла и А 2 лежит между А 1 и А 3 (рис.1).

Пусть B 1 В 2 , В 3 — соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если А 1 А 2 = A 2 A 3 , то В 1 В 2 = В 2 В 3 .

Проведем через точку В 2 прямую EF, параллельную прямой А 1 А 3 . По свойству параллелограмма А 1 А 2 = FB 2 , A 2 A 3 = B 2 E .

И так как А 1 А 2 = A 2 A 3 , то FB 2 = В 2 Е.

Треугольники B 2 B 1 F и В 2 В 3 Е равны по второму признаку. У них B 2 F = В 2 Е по доказанному. Углы при вершине В 2 равны как вертикальные, а углы B 2 FB 1 и B 2 EB 3 равны как внутренние накрест лежащие при параллельных А 1 В 1 и A 3 B 3 и секущей EF. Из равенства треугольников следует равенство сторон: В 1 В 2 = В 2 В 3 . Теорема доказана.

С использованием теоремы Фалеса устанавливается следующая теорема.

Теорема 2. Средняя линия треугольника параллельна третьей стороне и равна ее половине.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке 2 отрезок ED — средняя линия треугольника ABC.

ED — средняя линия треугольника ABC

Пример 1.
Разделить данный отрезок на четыре равные части.

Решение.

Пусть АВ — данный отрезок (рис.3), который надо разделить на 4 равные части.

Деление отрезка на четыре равные части

Для этого через точку А проведем произвольную полупрямую а и отложим на ней последовательно четыре равных между собой отрезка AC, CD, DE, ЕК.

Соединим точки В и К отрезком. Проведем через оставшиеся точки С, D, Е прямые, параллельные прямой ВК, так, чтобы они пересекли отрезок АВ.

Согласно теореме Фалеса отрезок АВ разделится на четыре равные части.

Пример 2.
Диагональ прямоугольника равна а. Чему равен периметр четырехугольника, вершины которого являются серединами сторон прямоугольника?

Решение.

Пусть условию задачи отвечает рисунок 4.

Тогда EF — средняя линия треугольника ABC и, значит, по теореме 2.
$$ EF = \frac{1}{2}AC = \frac{a}{2} $$

Аналогично $$
HG = \frac{1}{2}AC = \frac{a}{2} , EH = \frac{1}{2}BD = \frac{a}{2} , FG = \frac{1}{2}BD = \frac{a}{2}
$$ и, следовательно, периметр четырехугольника EFGH равен 2a.

Пример 3.
Стороны треугольника равны 2 см, 3 см и 4 см, а вершины его — середины сторон другого треугольника. Найти периметр большого треугольника.

Решение.

Пусть условию задачи отвечает рисунок 5.

Отрезки АВ, ВС, АС — средние линии треугольника DEF. Следовательно, согласно теореме 2 $$
AB = \frac{1}{2}EF\ \ ,\ \ BC = \frac{1}{2}DE\ \ ,\ \ AC = \frac{1}{2}DF
$$ или $$
2 = \frac{1}{2}EF\ \ ,\ \ 3 = \frac{1}{2}DE\ \ ,\ \ 4 = \frac{1}{2}DF
$$ откуда $$
EF = 4\ \ ,\ \ DE = 6\ \ ,\ \ DF = 8
$$ и, значит, периметр треугольника DEF равен 18 см.

Пример 4.
В прямоугольном треугольнике через середину его гипотенузы проведены прямые, параллельные его катетам. Найти периметр образовавшегося прямоугольника, если катеты треугольника равны 10 см и 8 см.

Решение.

В треугольнике ABC (рис.6)

∠ А прямой, АВ = 10 см, АС = 8 см, KD и MD — средние линии
треугольника ABC, откуда $$
KD = \frac{1}{2}AC = 4 см.
\\
MD = \frac{1}{2}AB = 5 см.
$$ Периметр прямоугольника К DMА равен 18 см.

Напечатать

Вариации и обобщения

Обратная теорема

Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:

Таким образом (см. рис.) из того, что
C
B
1
C
A
1
=
B
1
B
2
A
1
A
2
=
…
{\displaystyle {\frac {CB_{1}}{CA_{1}}}={\frac {B_{1}B_{2}}{A_{1}A_{2}}}=\ldots }
, следует, что
A
1
B
1
|
|
A
2
B
2
|
|
…
{\displaystyle A_{1}B_{1}||A_{2}B_{2}||\ldots }
.

Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).

Этой теоремой пользуются в навигации: столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется направление с одного судна на другое.

Лемма Соллертинского

Следующее утверждение, двойственно к лемме Соллертинского :

Пусть f {\displaystyle f} — проективное соответствие между точками прямой l {\displaystyle l} и прямой m {\displaystyle m} . Тогда множество прямых X f (X) {\displaystyle Xf(X)} будет множеством касательных к некоторому

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Доказательство. Пусть А 1 , А 2 , А 3 — точки пересечения параллельных прямых с одной из сторон угла и А 2 лежит между А 1 и А 3 (рис.1).

Пусть B 1 В 2 , В 3 — соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если А 1 А 2 = A 2 A 3 , то В 1 В 2 = В 2 В 3 .

Проведем через точку В 2 прямую EF, параллельную прямой А 1 А 3 . По свойству параллелограмма А 1 А 2 = FB 2 , A 2 A 3 = B 2 E .

И так как А 1 А 2 = A 2 A 3 , то FB 2 = В 2 Е.

Треугольники B 2 B 1 F и В 2 В 3 Е равны по второму признаку. У них B 2 F = В 2 Е по доказанному. Углы при вершине В 2 равны как вертикальные, а углы B 2 FB 1 и B 2 EB 3 равны как внутренние накрест лежащие при параллельных А 1 В 1 и A 3 B 3 и секущей EF. Из равенства треугольников следует равенство сторон: В 1 В 2 = В 2 В 3 . Теорема доказана.

С использованием теоремы Фалеса устанавливается следующая теорема.

Теорема 2. Средняя линия треугольника параллельна третьей стороне и равна ее половине.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке 2 отрезок ED — средняя линия треугольника ABC.

ED — средняя линия треугольника ABC

Пример 1.
Разделить данный отрезок на четыре равные части.

Решение.

Пусть АВ — данный отрезок (рис.3), который надо разделить на 4 равные части.

Деление отрезка на четыре равные части

Для этого через точку А проведем произвольную полупрямую а и отложим на ней последовательно четыре равных между собой отрезка AC, CD, DE, ЕК.

Соединим точки В и К отрезком. Проведем через оставшиеся точки С, D, Е прямые, параллельные прямой ВК, так, чтобы они пересекли отрезок АВ.

Согласно теореме Фалеса отрезок АВ разделится на четыре равные части.

Пример 2.
Диагональ прямоугольника равна а. Чему равен периметр четырехугольника, вершины которого являются серединами сторон прямоугольника?

Решение.

Пусть условию задачи отвечает рисунок 4.

Тогда EF — средняя линия треугольника ABC и, значит, по теореме 2.
$$ EF = \frac{1}{2}AC = \frac{a}{2} $$

Аналогично $$
HG = \frac{1}{2}AC = \frac{a}{2} , EH = \frac{1}{2}BD = \frac{a}{2} , FG = \frac{1}{2}BD = \frac{a}{2}
$$ и, следовательно, периметр четырехугольника EFGH равен 2a.

Пример 3.
Стороны треугольника равны 2 см, 3 см и 4 см, а вершины его — середины сторон другого треугольника. Найти периметр большого треугольника.

Решение.

Пусть условию задачи отвечает рисунок 5.

Отрезки АВ, ВС, АС — средние линии треугольника DEF. Следовательно, согласно теореме 2 $$
AB = \frac{1}{2}EF\ \ ,\ \ BC = \frac{1}{2}DE\ \ ,\ \ AC = \frac{1}{2}DF
$$ или $$
2 = \frac{1}{2}EF\ \ ,\ \ 3 = \frac{1}{2}DE\ \ ,\ \ 4 = \frac{1}{2}DF
$$ откуда $$
EF = 4\ \ ,\ \ DE = 6\ \ ,\ \ DF = 8
$$ и, значит, периметр треугольника DEF равен 18 см.

Пример 4.
В прямоугольном треугольнике через середину его гипотенузы проведены прямые, параллельные его катетам. Найти периметр образовавшегося прямоугольника, если катеты треугольника равны 10 см и 8 см.

Решение.

В треугольнике ABC (рис.6)

∠ А прямой, АВ = 10 см, АС = 8 см, KD и MD — средние линии
треугольника ABC, откуда $$
KD = \frac{1}{2}AC = 4 см.
\\
MD = \frac{1}{2}AB = 5 см.
$$ Периметр прямоугольника К DMА равен 18 см.

Огромные заслуги талантливого математика

В своё время Фалес Милетский был главным основателем Ионийской школы. Неоценимой заслугой этого человека было создание многофункциональной научной геометрии. Великий учёный специфического египетского искусства измерения смог самостоятельно создать полезную для человечества дедуктивную геометрию.

Благодаря целеустремлённости Фалеса все доступные в то время знания были оперативно переведены в научную категорию. Математик смог донести результаты своих наблюдений до того уровня, который подходит для учеников школ, указав при этом на определённый комплекс понятий. Доказанная талантливым и наблюдательным Фалесом теорема играет одну из самых важных ролей в геометрии. Она была хорошо известна не только в Древнем Египте, но и в других крупных странах. Актуальность и многогранность теоремы позволяет специалистам ежедневно строить новые здания, дороги и другие конструкции.

Фалес смог при помощи обычного посоха и тени установить габариты египетской пирамиды. Для этого он в обычный ясный день закрепил свой массивный посох на том участке, на котором заканчивалась тень от величественного сооружения. Он весь день прождал того момента, когда итоговая длина имеющейся тени от посоха максимально сравнялась с его высотой, после он измерил длину тени.