Аксиоматический метод

Понятие Теорема и Аксиома Лемма, Следствия с тестами кратко

Сразу хочу сказать, что здесь никакой воды про теорема, и только нужная информация. Для того чтобы лучше понимать что такое теорема, аксиома, лемма, следствия, аксиоматизация теории , настоятельно рекомендую прочитать все из категории введение в математику. основы. Кликните на вариант (или варианты ответов), если он правильный — то будет подсвечен зеленым цветом и вам будет зачислено пару монеток, а если неверный — то красным и будет снята монетка. Удачи в прохождении онлайн теста!

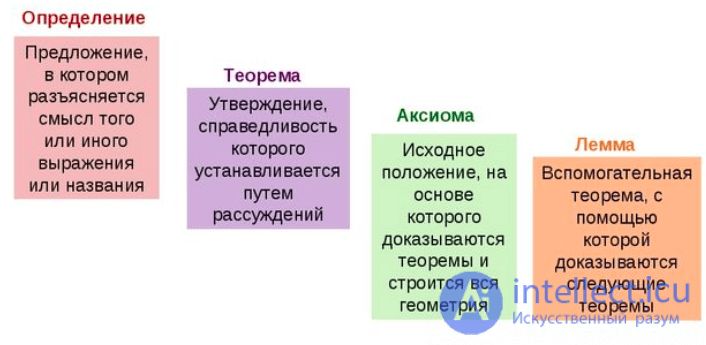
В математических дисциплинах широко используются четкие понятия такие как определения, теоремы, леммы, аксиомы, расссмотрим что это такое?

теорема (др.-греч. θεώρημα — «доказательство, вид; взгляд; представление, положение») — утверждение, для которого в рассматриваемой теории существует доказательство (иначе говоря, вывод). В отличие от теорем, аксиома ми называются утверждения, которые в рамках конкретной теории принимаются истинными без всяких доказательств или обоснований.

В математических текстах теоремами обычно называют только те доказанные утверждения, которые находят широкое применение в решении математических задач. При этом требуемые доказательства обычно кем-либо найдены (исключение составляют в основном работы по логике, в которых изучается само понятие доказательства, а потому в некоторых случаях теоремами называют даже неопределенные утверждения). Менее важные утверждения-теоремы обычно называют лемма ми,предложениями, следствия ми, условиями и прочими подобными терминами. Утверждения, о которых неизвестно, являются ли они теоремами, обычно называютгипотезами.

Наиболее знаменитыми являются теоремы Ферма, Пифагора и Птолемея.

Лемма (греч. λημμα — предположение) — доказанное утверждение, полезное не само по себе, а для доказательства других утверждений. Примеры известных лемм —лемма Евклида, лемма Жордана, лемма Гаусса, лемма Накаямы, лемма Гриндлингера, Лемма Лоренца, Лемма Лебедева.

Аксиома (др.-греч. ἀξίωμα — утверждение, положение), постула́т — исходное положение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства и используемое в основе доказательства других ее положений.

Необходимость в принятии аксиом без доказательств следует из индуктивного соображения: любое доказательство вынуждено опираться на какие-либо утверждения, и если для каждого из них требовать своих доказательств, цепочка получится бесконечной. Чтобы не уходить в бесконечность, нужно где-то эту цепочку разорвать — то есть какие-то утверждения принять без доказательств, как исходные. Именно такие, принятые в качестве исходных, утверждения и называются аксиомами.

В современной науке аксиомы — это те положения теории, которые принимаются за исходные, причем вопрос об истинности решается либо в рамках других научных теорий, либо посредством интерпретации данной теории.

Аксиоматизация теории — явное указание конечного или счетного, рекурсивно перечислимого (как, например, в аксиоматике Пеано) набора аксиом и правил вывода . Об этом говорит сайт https://intellect.icu . После того как даны названия изучаемым объектам и их основным отношениям, а также аксиомы, которым эти отношения должны подчиняться, все дальнейшее изложение должно основываться исключительно лишь на этих аксиомах, не опираясь на обычное конкретное значение этих объектов и их отношений. Утверждения на основе аксиом называются теоремами.

Примеры различных, но равносильных наборов аксиом можно встретить в математической логике и Евклидовой геометрии.

Набор аксиом называется непротиворечивым, если из аксиом набора, пользуясь правилами логики, нельзя прийти к противоречию, то есть доказать одновременно и некое утверждение, и его отрицание. Аксиомы являются своего рода «точками отсчета» для построения теорий в любой науке, при этом сами они не доказываются, а выводятся непосредственно из эмпирического наблюдения (опыта) или обосновываются в более глубокой теории.

Австрийский математик Курт Гедель доказал «теоремы о неполноте», согласно которым всякая система математических аксиом (формальная система) начиная с определенного уровня сложности либо внутренне противоречива, либо неполна (то есть в достаточно сложных системах найдется хотя бы одно высказывание, истинность и ложность которого не может быть доказана средствами самой этой системы).

• Аксиома выбора
• Аксиома параллельности Евклида
• Аксиома Архимеда
• Аксиома объемности
• Аксиома регулярности
• Аксиома полной индукции
• Аксиома Колмогорова
• Аксиома булеана

Индивидуальные доказательства

1. Quantity, Германн: Большой греческий немецкий словарь Лангеншайдса, Берлин, 1979 (23-е издание)
2. Питер Прехтль: Аксиома . В: Гельмут Глюк (ред.): Metzler Lexikon Sprache . JB Metzler Verlag GmbH, Штутгарт 2016, ISBN 978-3-476-02641-5 , стр.81 .
3. диссертация . В: Регенбоген, Мейер: Словарь философских терминов. 2005 г.
4. вывод . В: Регенбоген, Мейер: Словарь философских терминов. 2005 г.
5. Как у Тарского: Введение в математическую логику. 5-е издание. (1977), с. 127.
6. См. Карнап: Введение в символическую логику. 3. Издание. (1968), с. 172.
7. Так з. Б. Пол Руппен: Введение в формальную логику. Учебное пособие и тетрадь для нематематиков. Питер Ланг, Берн, 1996, с. 125.
8. ↑ Боченский: Современные методы мышления. 10-е изд. (1993), с. 79.
9. Bußmann: Лексикон лингвистики. 3-е издание, 2002 г., исчисление.
10. Иммануил Кант: Критика чистого разума . В: Бенно Эрдманн (Ред.): Издание Прусской Академии Наук . ЛентаIII . Георг Реймер, Берлин 1904 г., стр.480f .
11. Ульрих Фельгнер: «Основы геометрии» Гильберта и их место в истории фундаментальных дискуссий . В: Годовой отчет Немецкой ассоциации математиков . Лента115 , нет.3 , 2014, с.185-206 , DOI : .
12. ср. Б. Майкл Поттер: теория множеств и ее философия. Критическое введение. Oxford University Press, Oxford / New York 2004, p. 8.
13. Ср. Иосиф Мария Бохенский : Современные методы мышления. 10-е издание 1993 г., стр. 78 и т. Д.
14. Радуга / Мейер: Словарь философских терминов (2005) / Аксиома.
15. ↑ Seiffert: Theory of Science IV. 1997, начало.
16. Зайфферт: Теория науки IV.1997 , Аксиома.
17. Карнап: Введение в символическую логику. 3-е изд., 1968, с. 174.
18. Spree, in: Rehfus: Краткий словарь философии. 2003, аксиома.
19. См. Вводную и репрезентативную для состояния дискуссии в то время, Вольфганг Штегмюллер : Проблемы и результаты философии науки и аналитической философии, Том II: Теория и опыт, Вторая часть: Структуры теории и динамика теории. Springer, Berlin et al., 2-е изд., 1985, стр. 34 и далее.
20. См. Особенно Х. Райхенбах: Аксиоматика релятивистской теории пространства-времени. Vieweg, Брауншвейг, 1924 г.
21. О современных дискуссионных вопросах см. К. Брэдинг, Т. Рикман: «Основы физики» Гильберта: гравитация и электромагнетизм в рамках аксиоматического метода. В кн . : Исследования по истории и философии современной физики 39. 2008, 102–53.
22. См. А. А. Роб: Теория пространства и времени. Издательство Кембриджского университета, Кембридж, 1914.
23. См. К. Каратеодори: Об аксиоматике теории относительности. В кн . : Отчеты заседаний Прусской академии наук. Физико-математический класс 5. 1924, 12–27.
24. См. JCC McKinsey, AC Sugar, P. Suppes: Аксиоматические основы классической механики элементарных частиц. В: Журнал рациональной механики и анализа 2. 1953, стр. 253-272. Этот подход резюмируется в несколько измененной форме и обсуждается в Stegmüller, l. c., p. 106 ff.
25. См. Г. Хамель: Аксиомы механики. В: Х. Гейгер, К. Шил (Hrsg.): Handbuch der Physik, Том 5: Механика точек и твердых тел. Springer, Берлин, 1927, стр. 1-42.
26. См. Г. Людвиг: Интерпретация термина «физическая теория» и аксиоматическая основа структуры гильбертова пространства квантовой механики через основные принципы измерения. Конспект лекций по физике 4, Springer, Berlin 1970 and Ders .: Аксиоматическая основа квантовой механики. Том 1/2, Springer, Берлин, 1985/1987.
27. Опубликовано в 1964 году в A. Wightman, Ray Streater : PCT, Spin, Statistics и все такое. Карманная книга Университета BI 1964 ( PCT, Spin, Statistics и все такое. Бенджамин, Нью-Йорк 1964.)
28. См. Р. Джайлс: Математические основы термодинамики. Пергамон, Оксфорд, 1964.
29. См. Дж. Б. Бойлинг: Аксиоматический подход к классической термодинамике. В: Proceedings of the Royal Society of London 329. 1972, 35-71.
30. См. J. Jauch: На новом основании равновесной термодинамики. В: Основы физики 2. (1972), 327–332.
31. См. Э. Х. Либ, Дж. Ингвасон: Физико- математические аспекты второго закона термодинамики

Планиметрия — коротко о главном

Аксиомы принадлежности:

• Аксиома 1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
• Аксиома 2. Через любые две точки можно провести прямую, и только одну.

Аксиомы порядка:

• Аксиома 3. Из трех точек на прямой одна и только одна лежит между двумя другими.
• Аксиома 4. Прямая, лежащая в плоскости, разбивает эту плоскость на две полуплоскости. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.

Аксиомы мер для отрезков и углов:

• Аксиома 5. Каждый отрезок имеет определенную длину, больше нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
• Аксиома 6. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен \( \displaystyle 180{}^\circ \). Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Аксиомы существования треугольника, равного данному:

Аксиома 7. Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.

Следствие 1. От данной точки данной прямой в данную сторону можно отложить отрезок данной длины, причем единственным образом

Следствие 2. От данного луча в данную полуплоскость можно отложить угол данной величины, причем единственным образом

Аксиома параллельных:

Аксиома 8. На плоскости через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.

Основные факты об углах:

Теорема. Сумма смежных углов равна \( \displaystyle 180{}^\circ \).

\( \displaystyle 180{}^\circ=x_{1}^{{}^\circ }+x_{2}^{{}^\circ }\)

Теорема. Вертикальные углы равны.

\( \displaystyle \angle 1=\angle 2\).

Планиметрия — подробнее

Почему все в картинках и без слов? А нужны ли слова? Мне кажется, на первых порах не очень нужны.

Описания ты найдешь далее в этой статье, а сейчас продолжим картинками.

Что же еще? Ах да, нам же нужно научиться измерять отрезки и углы.

У каждого отрезка есть длина – число, которое этому отрезку (зачем-то …) поставили в соответствие. Длину принято измерять … линейкой, конечно, в сантиметрах, миллиметрах, метрах и даже в километрах.

А теперь измерение углов. Углы почему-то принято измерять в градусах. Почему? На это есть исторические причины, но мы сейчас занимаемся не историей. Поэтому придется принять просто как должное следующее соглашение.

Для краткости пишут: \( \displaystyle {{180}^{\circ }}\). При этом, конечно же, величину всех остальных углов можно найти, если выяснить, какую часть от развернутого угла составляет данный угол.

Инструмент для измерения углов называется транспортир. Думаю, ты его уже не раз в жизни видел.

Теоретические материалы

Планиметрия

1. Введение

1.1. Понятие об аксиоме и теореме

Наука начинается с установления понятий, геометрия — с понятий геометрическое тело (часть пространства, ограниченная со всех сторон); поверхность (граница тела), в частности плоскость; линия (граница поверхности), в частности прямая линия; точка (общая часть двух встречающихся прямых). Плоскость и прямую можно продолжать неограниченно, они не имеют толщины. В дальнейшем понятия вводятся с помощью определений.

Определение

Любую совокупность точек, линий, поверхностей и тел называют фигурой. В геометрии изучают свойства фигур.

Результат изучения свойств фигур (или чисел, величин, их соотношений, операций над ними) выражается математическим предложением.

Определение

Математическое предложение, правильность которого доказывается, называют теоремой.

Определение

Математическое предложение принимаемое без доказательства, называют аксиомой.

Приведем аксиомы, выражающие свойства прямой, плоскости и отрезка.

Аксиома 1

Через две точки можно провести прямую линию и притом только одну.

Аксиома 2

Если две точки прямой принадлежат плоскости, то и каждая точка этой прямой принадлежит плоскости.

Аксиома 3

Отрезок прямой короче всякой другой линии (ломаной или кривой), соединяющей его концы.

Расстояние между двумя точками измеряется по прямой линии. В геометрии используются еще и такие аксиомы, которые уже применялись в арифметике и алгебре (сформулируем их для произвольных величин , и ):

Аксиома 4

Если и , то .

Аксиома 5

Если , то и .

Теорема состоит из условия (того, что дано) и заключения (утверждения, которое требуется доказать). Условие может начинаться словом «если», а заключение — словом «то». Теоремы, например: «Вертикальные углы равны», «Углы при основании равнобедренного треугольника равны» можно сформулировать так: «Если углы вертикальные, то они равны», «Если треугольник равнобедренный, то углы при основании равны».

Если условие данной теоремы сделать заключением, а заключение — условием, то первая теорема будет прямой, а полученная — обратной теоремой.

Теоремы, обратные приведенным выше: «Если углы равны, то они вертикальные», «Если углы при основании треугольника равны, то треугольник равнобедренный». Первая из этих теорем неверна, хотя ее прямая теорема верна. Каждая обратная теорема требует своего доказательства.

Определение

Предложение, непосредственно вытекающее из теоремы, называют следствием.

Определение

Вспомогательную теорему, которая вводится для облегчения доказательства основной теоремы, называют леммой.

16.4. Аксиомы и теоремы в геометрии window.top.document.title = «16.4. Аксиомы и теоремы в геометрии»;

Как было отмечено ранее, изучение геометрии основано на аксиоматическом методе. После формулировки основных понятий и аксиом все дальнейшие результаты теории – результаты логических рассуждений, которые оформляются в виде определенного вида утверждений. Рассмотрим это более подробно.

Теорема – утверждение, требующее доказательства. Таковыми являются, например, теоремы 1.1 и 1.2.

Лемма – вспомогательная теорема, которая приводится для того, чтобы с ее помощью доказать следующую теорему или группу теорем. Например, с помощью леммы 1.1 мы доказали теорему 1.2.

Следствие (из определения, теоремы, аксиомы) – теорема, которая позволяет более полно трактовать содержание данной теоремы, аксиомы, определения. Например, следствие 1.1 раскрывает дополнительные свойства двух прямых на основании аксиомы 1.2; следствие 1.2 – свойства точек, принадлежащих разным полуплоскостям, следующие непосредственно из определения 1.9 и аксиомы 1.6. Таким образом, основным средством познания (выяснения новых свойств геометрических фигур) в геометрии является доказательство теорем.

Рассмотрим, например, формулировку теоремы, данную в следствии 1.1: если на луче отложить от начальной его точки два отрезка AB и AC и если AB = AC, то точки B и C совпадут. Условием теоремы является предложение {на луче отложить от начальной его точки два отрезка AB и AC и AB = AC}. Это предложение не является в данном виде высказыванием, но содержит описание множества объектов, относительно которых делается высказывание вида AB = AC. Из описания ясно, что речь идет о множестве отрезков луча a, отложенных от начальной его точки. Поскольку один конец отрезка фиксирован, то отрезок определяется однозначно точкой луча. Обозначим как P множество точек луча, отличных от его начальной точки. Пусть B  P – заданная точка. Тогда условие теоремы является предложением относительно точки множества P. Перепишем условие теоремы в виде: A (x) = {длина отрезка Ax = AB}. Очевидно, это предикат. Заключение теоремы есть предикат B (x) = {точка x совпадает с точкой B}. Тогда теорему можно переформулировать следующим образом: если x – произвольная точка луча AB такая, что Ax = AB, тогда точка x совпадает с точкой B, которую можно записать в виде

Утверждается, что любую теорему можно записать в таком виде (мы показали на данном примере, как это можно сделать в частном случае), поэтому проанализируем структуру теоремы.В ней можно выделить три части:

1. Условие теоремы: предикат A (x), заданный на множестве точек луча AB, без его начальной точки.
2. Заключение теоремы: предикат B (x), заданный на множестве точек луча AB за исключением точки A.
3. Разъяснительная часть: в ней описывается множество объектов, о которых идет речь в теореме.

В символической записи теоремы к разъяснительной части теоремы следует отнести запись

Пусть  – запись истинной теоремы. Тогда ее условие и заключение образуют импликацию, истинную при всех x из множества X, и, следовательно, предикат B (x) логически следует из предиката A (x). Поэтому заключение теоремы B (x) является необходимым условием для условия A (x), а условие A (x) – достаточным для заключения теоремы B (x).

Определение 16.30. 

Пусть A (x) и B (x) – два предиката, заданные на множестве X. Тогда теоремы  и  называются обратными друг к другу.

Определение 16.31. 

Если истинны обе теоремы  и  то говорят, что каждый из предикатов A (x) и B (x) является необходимым и достаточным условием другого. Обе теоремы при этом можно объединить в одну теорему вида

Пусть дана теорема

Определение 16.32. 

Теорема  называется противоположной к данной.

Определение 16.33. 

Теорему  называют теоремой, противоположной обратной.

Теорема 16.1. 

Теорема  равносильна противоположной обратной.

На основании этого утверждения основан метод доказательства от противного. Суть этого метода состоит в том, что доказывают истинность теоремы, противоположной обратной, поскольку если эта теорема истинна, то и исходная теорема тоже верна.

Сайт знакомств: чат рулетка с девушками 18 . Видеочат онлайн.

virtruletka18.ru

Понятие аксиомы

Аксиома — это правило, которое считают верным и которое не нужно доказывать. В переводе с греческого «аксиома» значит принятое положение — то есть взяли и договорились, что это истина, с которой не поспоришь.

Аксиоматический метод — это подход к получению знаний, при котором сначала разрабатывают аксиомы, а потом с их помощью формулируют новые теории.

Синоним аксиомы — постулат. Антоним — гипотеза.

Основные аксиомы евклидовой геометрии

Через любые две точки проходит единственная прямая.
Каждая точка на прямой разбивает эту прямую на две части так, что точки из разных частей лежат по разные стороны от данной точки. А точки из одной части лежат по одну сторону от данной точки.
На любом луче от его начала можно отложить только один отрезок, равный данному.
Отрезки, полученные сложением или вычитанием соответственно равных отрезков — равны.
Каждая прямая на плоскости разбивает эту плоскость на две полуплоскости. При этом если две точки принадлежат разным частям, то отрезок, который соединяет эти две точки, пересекается с прямой. Если две точки принадлежат одной части, то отрезок, соединяющий эти точки, не пересекается с прямой.
От любого луча на плоскости в заданную сторону можно отложить только один угол, который равен данному. Все развернутые углы равны.
Углы равны, если они получились путем сложения или вычитания соответственно равных углов.

Учить наизусть эти аксиомы не обязательно. Главное — помнить о них и держать под рукой, чтобы при доказательстве теоремы сослаться на одну из них.

А теперь давайте рассмотрим несколько аксиом из геометрии за 7 и 8 класс.

Самая известная аксиома Евклида — Аксиома о параллельных прямых. Звучит она так:

Это значит, что если дана прямая и любая точка, которая не лежит на этой прямой, то через неё можно провести только одну единственную прямую, которая будет параллельна этой первой данной прямой.

У этой аксиомы два следствия:

• прямая, которая пересекает одну параллельную прямую, обязательно пересекает и другую; если две прямые параллельны третьей, то между собой они также параллельны.

Аксиома Архимеда заключается в том, что, если отложить достаточное число раз меньший из двух отрезков, то можно покрыть больший из них. Звучит так:

Если на прямой есть меньший отрезок А и больший отрезок B, то, можно сложить А достаточное количество раз, чтобы покрыть B.

На картинке можно увидеть, как это выглядит:

Из этого следует, что не существует бесконечно малых и бесконечно больших величин. В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Реши домашку по математике на 5. Подробные решения помогут разобраться в самой сложной теме. Получить

Разграничения

В рамках теории, которую можно формализовать, тезис — это утверждение, которое необходимо доказать. С другой стороны, аксиома — это утверждение, которое не предполагается доказывать теоретически, но предполагается без доказательства. Если выбранные аксиомы теории логически независимы , ни одна из них не может быть выведена из других. Аксиомы этого исчисления всегда можно вывести в рамках формального исчисления . В формальном или синтаксическом смысле это доказательство ; С семантической точки зрения это круговой аргумент . В противном случае применяется следующее: «Если вывод основан на аксиомах исчисления или на истинных утверждениях, то говорят о доказательстве».

Аксиома используется как противоположность теореме (в более узком смысле). Теоремы и аксиомы — это теоремы формализованного исчисления, которые связаны производными отношениями. Теоремы — это теоремы, выведенные из аксиом с помощью формальных доказательств. Иногда, однако, термины тезис и теорема используются в более широком смысле для всех действительных утверждений формальной системы, т. Е. ЧАС. как общий термин, который включает в себя как аксиомы, так и теоремы в первоначальном смысле.

Таким образом, аксиомы можно понимать как условия полной теории , поскольку они могут быть выражены в формализованном исчислении. В рамках интерпретируемого формального языка различные теории можно выделить путем выбора аксиом. В случае неинтерпретируемых исчислений формальной логики вместо теорий говорят о логических системах, которые полностью определяются аксиомами и правилами вывода . Это релятивизирует концепцию выводимости или доказуемости: она всегда существует только по отношению к данной системе. Аксиомы и производные утверждения принадлежат , правила — метаязыку .

Однако исчисление не обязательно является аксиоматическим исчислением, которое, следовательно, состоит из «набора аксиом и минимально возможного набора правил вывода». Есть также и табличные исчисления .

Иммануил Кант называет аксиомы «синтетическими принципами априори, если они непосредственно достоверны» и этим определением исключает их из области философии. Это основано на концепциях, которые, как абстрактные образы, никогда не имеют никаких свидетельств в качестве объекта непосредственной интуиции. Таким образом, он отличает дискурсивные принципы философии от интуитивных принципов математики: первые должны «чувствовать себя комфортно, обосновывая свой авторитет на их основе тщательной дедукцией» и, следовательно, не соответствуют критериям априори.

Аксиомы стереометрии с рисунками

Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Аксиома 2. Если две точки прямой лежат в плоскости, то все точки данной прямой лежат в этой плоскости. В этом случае говорят, что прямая лежит в плоскости или что плоскость проходит через прямую.

Аксиома 3. Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей. В этом случае говорят, что плоскости пересекаются по прямой.

Аксиома 4. В любой плоскости пространства выполняются все аксиомы планиметрии. Таким образом, в любой плоскости пространства можно использовать все доказанные теоремы и формулы из планиметрии.

Следствия из аксиом

Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.

Следствие 2. Через две пересекающиеся прямые проходит плоскость и притом только одна.

Следствие 3. Через две параллельные прямые проходит плоскость и притом только одна.

Следствие 4. Из аксиомы (математическое утверждение не требующее доказательства) 2 следует, что прямая, не лежащая в плоскости, не может иметь с плоскостью более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость.

Понятие теоремы

Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.

Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.

Состав теоремы: условие и заключение или следствие.

Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.

Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.

Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.

Примеры следствий из аксиомы о параллельности прямых:

• если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую; если две прямые параллельны третьей прямой, то они параллельны.

Доказательство теоремы — это процесс обоснования истинности утверждения.

Каждая доказанная теорема служит основанием доказательства для следующей теоремы

Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам

Способы доказательства геометрических теорем

• Синтетический или синтез — метод, при котором данное предложение выступает, как необходимое следствие другого, уже доказанного. Аналитический или анализ — обратный синтезу способ. Рассуждения всегда начинаются с доказываемой теоремы и закачиваются другой известной истиной.

Часть аналитического способа — Доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.

Приемы для доказательства в геометрии:

• Способ наложения — когда одну геометрическую величину накладывают на другую. Этим способом убеждаются в равенстве или неравенстве геометрических протяжений в зависимости от того, совмещаются они или нет при наложении. Способ пропорциональности — применение свойств пропорций. Этот способ пригодится для доказательства теорем про подобные фигуры и пропорциональные отрезки. Способ пределов — когда вместо данной величины берут свойства другой, близкой к ней. А потом перекладывают эти выводы на исходные данные.

Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.

Прямая и обратная теорема взаимно-обратные. Например:

• прямая теорема: в треугольнике

Против равных сторон лежат равные Углы. обратная теорема: в треугольнике Против равных углов лежат равные Стороны.

В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов. А во второй всё наоборот.

Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.

Вот, как выглядит взаимное отношение теорем на примере:

• Прямая: если при пересечении двух прямых третьей соответственные углы равны, то данные прямые параллельны. Обратная: если две прямые параллельны, то при пересечении их третьей, соответственные углы равны. Противоположная: если при пересечении двух прямых третьей соответственные углы не равны, прямые не параллельны. Обратная противоположной: если прямые не параллельны, соответственные углы не равны.

В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Основные понятия введения в стереометрию

Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.

Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два из которых, имеющие общую сторону, не лежат в одной плоскости. При этом сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника.

Фигура, образованная всеми гранями многогранника, называется его поверхностью (полной поверхностью), а сумма площадей всех его граней – площадью (полной) поверхности.

Куб – это многогранник, имеющий шесть граней, которые являются равными квадратами. Стороны квадратов называются ребрами куба, а вершины – вершинами куба.

Параллелепипед – это многогранник, у которого шесть граней и каждая из них – параллелограмм. Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра, а имеющие общее ребро называются смежными. Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, – его боковыми ребрами.

Прямой параллелепипед – это такой параллелепипед, у которого боковые грани – прямоугольники.

Прямоугольный параллелепипед – это параллелепипед, у которого все грани – прямоугольники. Заметим, что всякий прямоугольный параллелепипед является прямым параллелепипедом, но не любой прямой параллелепипед есть прямоугольный.

Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий противолежащие вершины параллелепипеда, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.

Призма (n-угольная) – это многогранник, у которого две грани – равные n-угольники, а остальные n граней – параллелограммы. Равные n-угольники называются основаниями, а параллелограммы – боковыми гранями призмы.

Прямая призма – это такая призма, у которой боковые грани – прямоугольники. Правильная n-угольная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильные n-угольники.

Сумма площадей боковых граней призмы называется площадью ее боковой поверхности (обозначается Sбок). Сумма площадей всех граней призмы называется площадью поверхности призмы (обозначается Sполн).

Пирамида (n-угольная) – это многогранник, у которого одна грань – какой-нибудь n-угольник, а остальные n граней – треугольники с общей вершиной; n-угольник называется основанием; треугольники, имеющие общую вершину, называются боковыми гранями, а их общая вершина называется вершиной пирамиды. Стороны граней пирамиды называются ее ребрами, а ребра, сходящиеся в вершине, называются боковыми.

Сумма площадей боковых граней пирамиды называется площадью боковой поверхности пирамиды (обозначается Sбок). Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается Sполн).

Правильная n-угольная пирамида – это такая пирамида, основание которой – правильный n-угольник, а все боковые ребра равны между собой. У правильной пирамиды боковые грани – равные друг другу равнобедренные треугольники.

Треугольная пирамида называется тетраэдром, если все ее грани – равные правильные треугольники. Тетраэдр является частным случаем правильной треугольной пирамиды (т.е. не каждая правильная треугольная пирамида будет тетраэдром).