Тригонометрия: таблица косинусов, синусов, тангенсов и катангенсов

Определение значения синуса, косинуса, тангенса и котангенса

Определение

Тригонометрия — это техническая часть математики, в которой представлены особенности взаимосвязи между сторонами и углами треугольников.

Тригонометрические функции, является очень важной составляющей не только математики, но других технических наук. Применяя основные формулы и законы тригонометрии при вычислении задач

Огромное значение имеют таблицы значений данных функций. Они существенно упрощают решение задач различной сложности.

Применяя основные формулы и законы тригонометрии при вычислении задач. Огромное значение имеют таблицы значений данных функций. Они существенно упрощают решение задач различной сложности.

Процесс работы и расчета функций данного вида, очень непростой. Решение задач и уравнение, очень часто вызывают сложности. Поэтому, со временем, были созданы и разработаны несколько видов решений, чтобы облегчить жизнь математика и всем представителям технических наук. Преобразовывая тригонометрические формулы, необходимо руководствоваться следующими правилами:

Нельзя продумывать весь процесс решения от начала до самого конца сразу. Нужно определиться с основными задачами и данными.
Весь пример, подвергать упрощению или преобразования постепенно;
Разрешается применять все преобразования и действия, связанные с алгеброй, а именно: вынести значение за пределы скобок. сократить значение и многое другое:

Зная основные определения тригонометрических функций, можно определить их угловые значения. Для углов от нуля до трехсот шестидесяти градусов, вычислим данные и запишем их в виде таблицы.

Значения вышеупомянутых математических функций, в частности в разделе геометрия, вычисляются как соотношения длин прямоугольного треугольника.

Углы геометрической фигуры имеют соответствующие значения в градусах. Используя основные определения математики, а именно тригонометрии можно определить нужные нам данные.

Определим основные значения

1.синуса (sin):

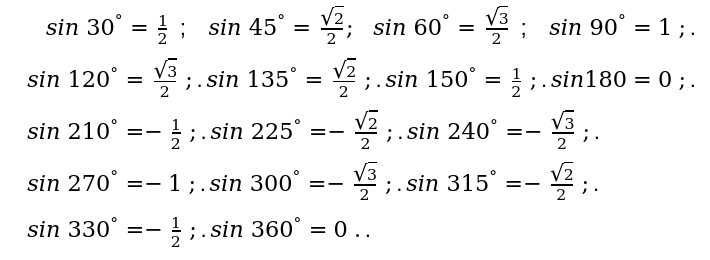
2. косинуса (cos):

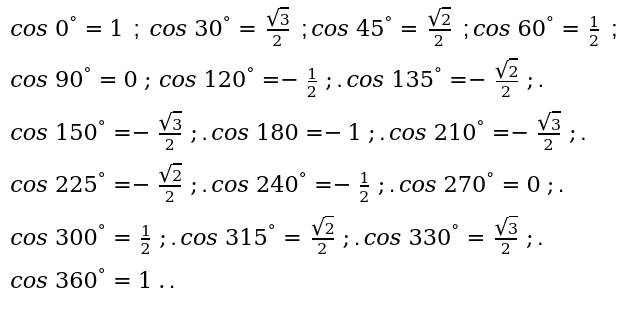
3. тангенса(tg):

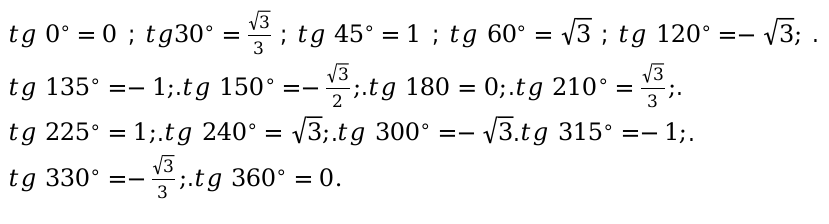
Данные выше угловые значения, не определяются, согласно основным законам геометрии и математики.

4. котангенса (ctg)

Для перечисленных выше угловых значений по законам математики и всех технических наук в целом, значения не определяются

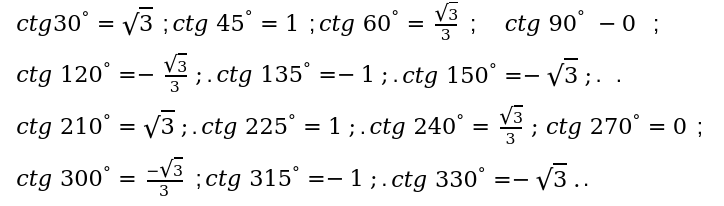
Мы произвели основные расчеты. Определили результаты угловых значений.

Мы определились с основными угловыми значениями функций. Следующим шагом будет их сведение в таблицу.

Таблица1. Основные значения функций косинус, синус, тангенс и котангенс, для угловых значений и радиан

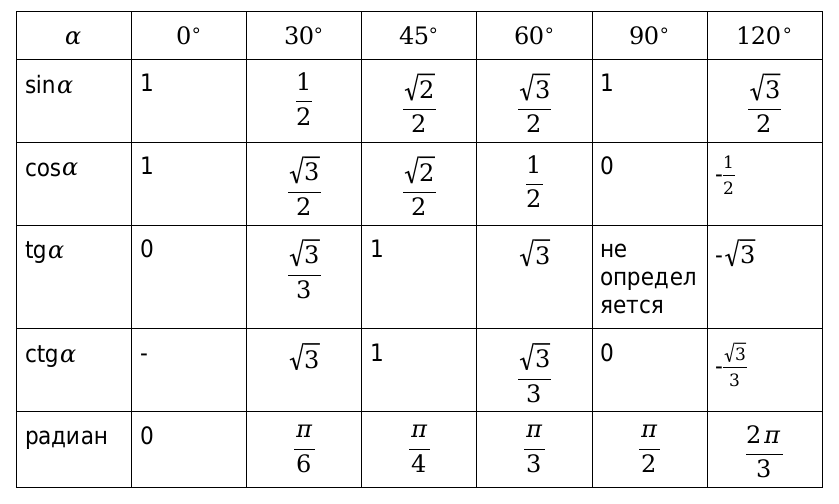
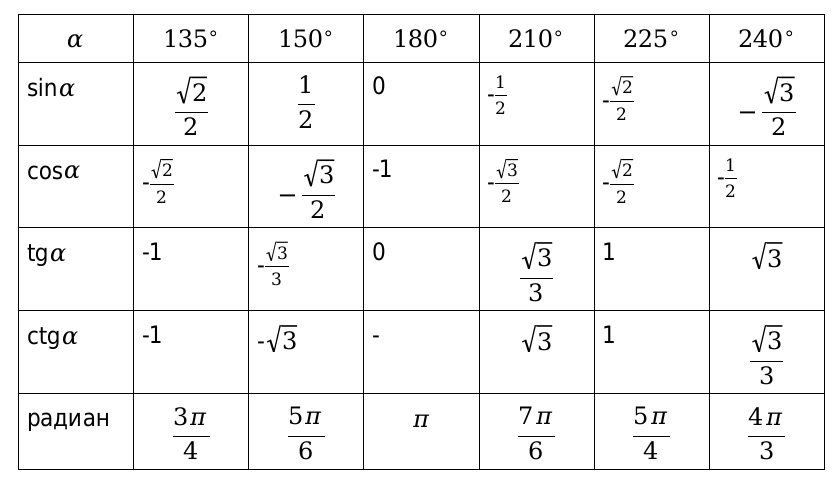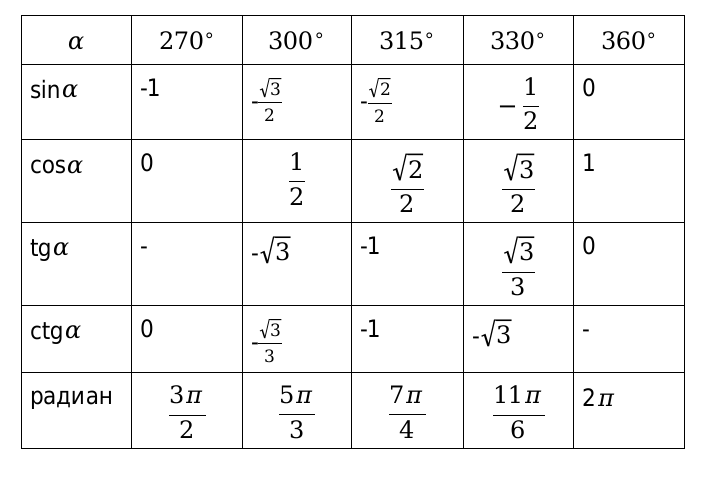Продолжение таблицы 1

Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более лучшего восприятия. Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.

Таблица 2. Нестандартные углы функций косинус, синус, тангенс и котангенс в тригонометрии

В данной таблице приведены значения углов, которые считаются нестандартными, также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.

Например:

Значение заданной функции берется из таблицы. Оно равняется данному, которое попадает на пересечение столбца и строки.

Пример №1. Необходимо определить чему равен \

Берем левый столбец с наименованием функции, находим в верхней строке нужный градус, и на пересечении определяем нужный ответ.

Следовательно:\.

Пример №2. Необходимо определить чему равен \.

Берем левый столбец с наименованием функции, находим в нижней строке значение радиан, поднимается на верх таблицы и определяем градусы.

Пример №3. Необходимо определить чему равен \.

Проводим аналогичные действия, как в предыдущих двух примерах и определяем угловое значение.

Тригонометрический круг

Графически соотношение упомянутых величин можно представить следующим образом:

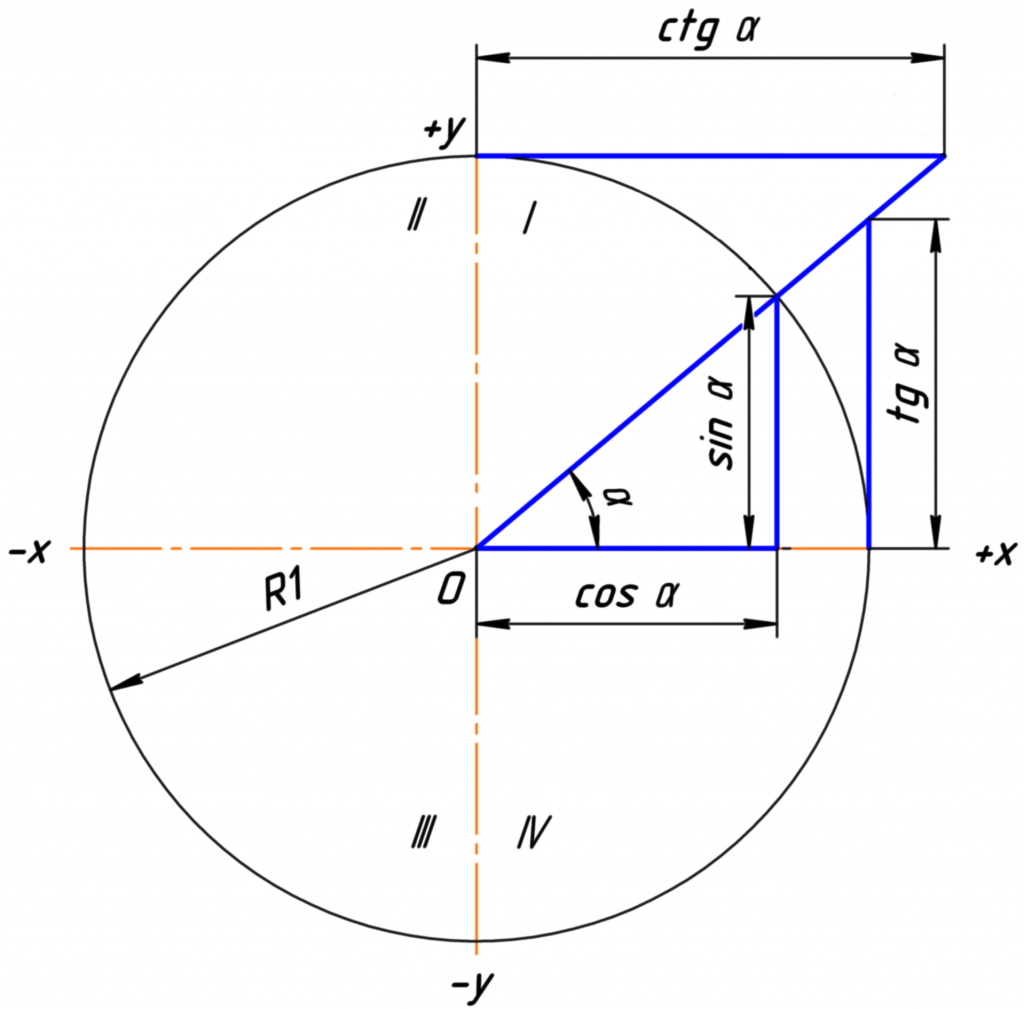
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.

Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.

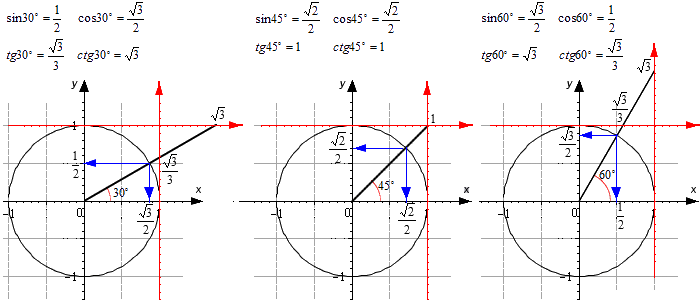
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.

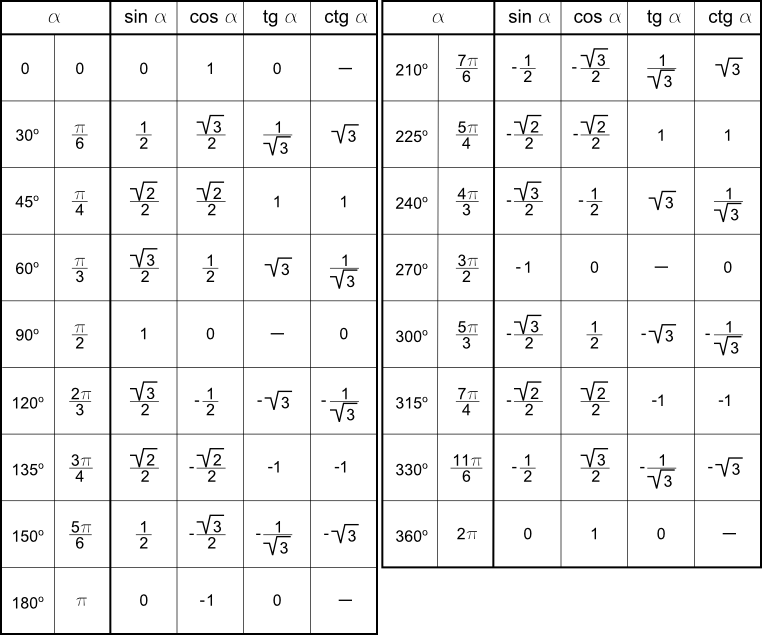
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.

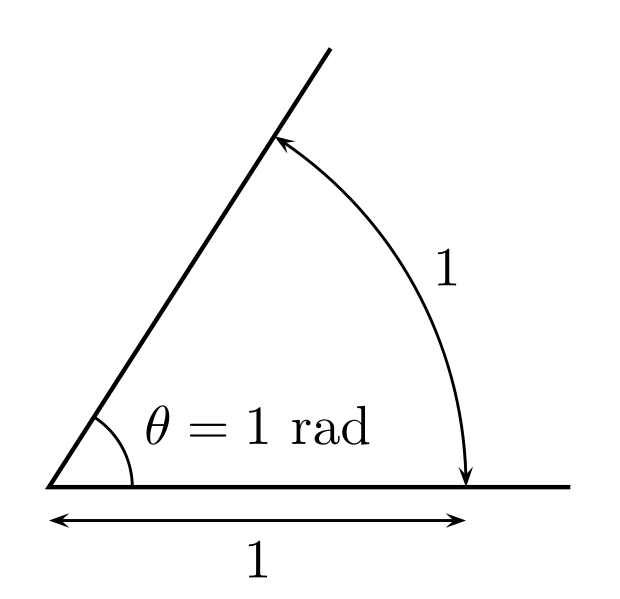
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:

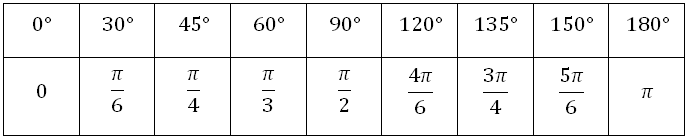
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.

Вычисление данных при помощи фигуры — прямоугольный треугольник

Для этого строится нужный треугольник заданным углом, который необходимо определить. Строится угол, точка и луч, которые выходят из данной точки под определенным углом. Соединяем лучи, прямой линией перпендикулярной, одному из лучей. В конечном итоге получаем фигуру, угол которой равняется заданному в задаче углу. В процессе вычисления, также задаются длины сторон. Поэтому трудней с построением не должно возникнуть.

Вычисление при помощи длин сторон треугольника происходит следующим образом:

обозначается катет;
сторона возле угла;
сторона напротив угла с прямым значением.

Функции могут выражаться по-разному в отношении сторон. Например, нам нужно определим значение sin 45°. Поделим имеющуюся длину значения противолежащего катета на значение длины гипотенузы. Если заданные значения длины равны 4 и 6 соответственно. Тогда, составим следующее выражение и получим sin\

Для определения значений основных функций в математике, необходимо заучить наизусть определение основных понятий, связанный с данной темой.

В процессе решения задачи, это придется применять постоянно.

Значения косеканса и секанса определяются в обратном порядке. Для этого необходимо знать какие стороны нужно делить для определения вышеперечисленных функций.

Косеканс находится \ следовательно, нужно разделить гипотенузу на противолежащий катет. Секанс, наоборот к прилежащему катету \.

Например, для определения cosec 40°, если катет равен 5, а гипотенуза соответственно равна 8. Нужно разделить 5/8 и получим ответ cosec 40° = 0,63.

При вычислениях всегда рекомендуется исключать значение под корнем в знаменателе, это наиболее облегчает процесс расчета.

Рассмотренная тема преобразования и расчета функций, является довольно громоздкой, на первый взгляд. Применяя для решения огромные формулы и функции можно растеряться и не сразу сообразить, как производить их расчет. Однако досконально рассмотрев и изучив каждый раздел, становится понятно, что все достаточно просто и громоздкие таблицы освоить можно быстро и легко.

Значения от 181 до 360 градусов

Таблицы Брадиса дают значения для углов от 0° до 90°. Остальные величины можно легко найти с помощью формул приведения. В этом случае угол, величину которого необходимо узнать, представляется как сумма (или разность) угла, кратного 90° и острого угла, например, для 140° это будет:

90° + 50°;
180° — 40°.

Формулы приведения, которые используются в этом случае, имеют вид:

$\sin\;(90^\circ\;+\;a)\;=\;\cos\;a,\;\sin\;(180^\circ\;-\;\beta)\;=\;\sin\;a$;
$\cos\;(90^\circ\;+\;a)\;=\;-\sin\;a,\;\cos\;(180^\circ\;-\;\beta)\;=\;-\cos\;a$;
$tg\;(90^\circ\;+\;a)\;=\;-ctg\;a,\;tg\;(180^\circ\;-\;\beta)\;=\;-tg\;a$;
$ctg\;(90^\circ\;+\;a)\;=\;-tg\;a,\;ctg\;(180^\circ\;-\;\beta)\;=\;-ctg\;a$.

Для примера можно провести расчет для ситуации, когда угол в 140° представлен как 90° + 50°:

$\sin\;(90^\circ\;+\;50^\circ)\;=\;\cos\;50^\circ\;=\;0,6428$;
$\cos\;(90^\circ\;+\;50^\circ)\;=\;-\sin\;50^\circ\;=\;-0,7660$;
$tg(90^\circ+50^\circ)=-ctg50^\circ=-0,8391$;
$ctg\;(90^\circ\;+\;50^\circ)\;=\;tg\;50^\circ\;=\;1,1918$.

Стандартные углы

Итак, значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $ и $\operatorname{ctg}\alpha $ однозначно определяются величиной угла $\alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.

Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:

Для большинства углов $\alpha $ нельзя найти точные значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $.
Верно и обратное: для большинства «красивых» $\sin \alpha $, $\cos \alpha $ и т.д. нельзя подобрать подходящий угол $\alpha $.

Звучит немного непонятно, поэтому разберём каждый пункт на конкретных примерах.

3.1. Три стандартных угла

Существует лишь три острых угла, для которых легко считаются синусы, косинусы и т.д. Это 30°, 45°, 60°. Вот их синусы, косинусы и тангенсы:

Чтобы понять, чем эти углы такие особенные, просто посчитаем все эти синусы, косинусы и тангенсы. Начнём с $\alpha =45{}^\circ $. Для этого рассмотрим равнобедренный прямоугольный треугольник. Мы уже встречались с ним:

Поскольку в равнобедренном треугольнике $\angle A=\angle B=45{}^\circ $, получим:

Это именно те значения, которые указаны в таблице!

Теперь разберёмся с углами $\alpha =30{}^\circ $ и $\alpha =60{}^\circ $. Здесь рассуждения будут чуть сложнее. Сначала рассмотрим равносторонний треугольник $ABC$ со стороной $AB=2$ (просто так удобнее) и проведём высоту $BH$:

Мы знаем, что высота $BH$ — ещё и медиана, и биссектриса. Поэтому $AH=CH=1$, $\angle ABH=\angle CBH=30{}^\circ $.

Следовательно, треугольник $ABH$ — прямоугольный, да ещё и с острыми углами 30° и 60°. По теореме Пифагора легко найти $BH=\sqrt{3}$. Нанесём все данные на чертёж:

Разберёмся с углом 60°:

И с углом 30°:

Попробуйте повторить все эти рассуждения самостоятельно. Это очень полезное упражнение!

Возникает вопрос: как быть с другими углами? Например, можно ли найти $\sin {50}^\circ $? Или, быть может, $\cos {10}^\circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.

Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?

3.2. Что с другими углами?

Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:

Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $\alpha $:

Итак, мы знаем синус

Внимание, вопрос: каким должен быть угол $\alpha $, чтобы $\sin \alpha =0,6$? Сколько градусов должно быть в угле $\alpha $? Ответ: неизвестно.:). Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$

Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует

Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.

Из всех этих рассуждений сделаем важный вывод. В тригонометрии мы:

Либо берём угол и считаем для него синусы, косинусы и т.д. Но лишь для трёх острых углов — 30°, 45°, 60° — всё будет считаться быстро и красиво. Такие углы называются табличными.
Либо берём синус, косинус или тангенс и для него пытаемся подобрать острый угол. Но лишь для табличных значений мы сможем подобрать такие углы. И да: это будут углы 30°, 45°, 60°.

Ещё раз:

И наоборот:

С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.

Что такое таблицы тригонометрических функций

Определение

Тригонометрические функции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе.

Для определения неизвестных элементов треугольника (сторон или углов), необходимо использовать известные элементы и правила зависимости между ними. Подобные зависимости называют также тригонометрическими функциями. Таким образом, зная значения некоторого угла или стороны, пользуясь тригонометрическими функциями можно найти неизвестные углы и стороны треугольника. Именно поэтому, без знаний тригонометрии решать геометрические задачи не представляется возможным.

Основные тригонометрические функции:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Синус — отношение противолежащего катета к гипотенузе.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к прилежащему. Также равен частному от деления синуса определенного угла на его косинус.
Котангенс — отношение прилежащего катета к противолежащему. Также равен частному от деления косинуса определенного угла на его синус.

Примечание

Синус и косинус являются прямыми тригонометрическими функциями, тангенс и котангенс — производными. Существуют и другие тригонометрические функции, например — арктангенс. Арктангенс относится к так называемым обратным тригонометрическим функциям, и является функцией, обратной тангенсу. Это означает, что если тангенс некоторого угла у градусов (радиан) равен х, значит арктангенс x равняется y градусов (радиан).

Вычисленные тригонометрические функции (синус, косинус и тангенс) представляют в виде специальных таблиц, которые можно использовать при решении задач — это и есть таблицы тригонометрических функций. В них приведены значения тригонометрических функций углов от 0° до 360°.

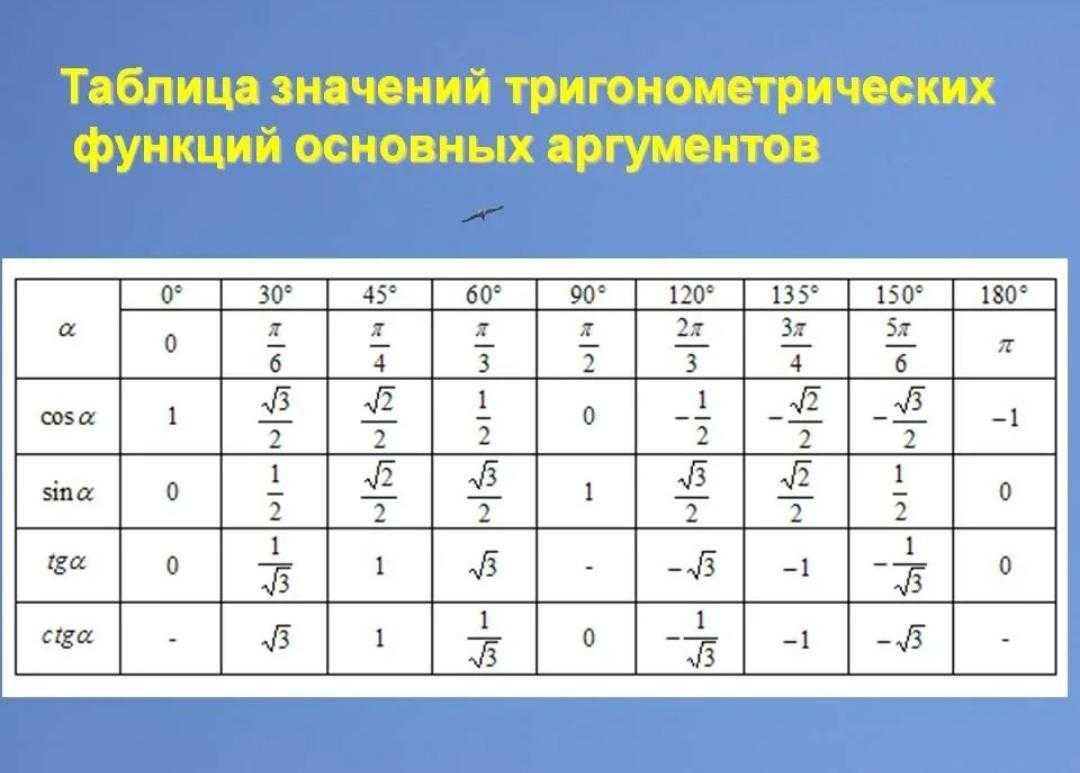
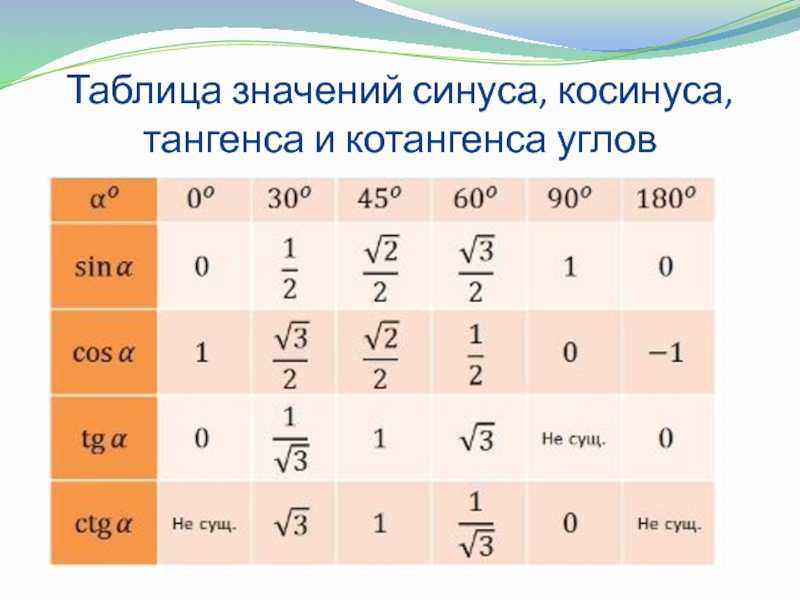
Для прямоугольных треугольников в диапазоне углов от 30° до 90° тригонометрические функции равняются следующим значениям:

sin 30° = 1/2, cos 30° = √3/2, tg 30° = √3/3, ctg 30° = √3
sin 45° = √2/2, cos 45° = √2/2, tg 45°= 1, ctg 45° = 1
sin 60° = √3/2, cos 60° = 1/2, tg 60° =√3 , ctg 60° = √3/3

Как выглядит для значений, синуса, косинуса, тангенса и котангенса

Таблица тригонометрических функций выглядит следующим образом:

Значение аргумента α задано в верхней строке задано в градусах (от 0° до 90°), во второй строке — в радианах (0, π/6, π/4, π/3, π/2 радиан). Иногда в таблице присутствуют значения только в радианах. Для перевода в градусы необходимо подставить число π = 180°, например, π/6 = 180/6 = 30°.

Обозначение «не определен» в таблице (тангенс 90° и котангенс 0°) означает, что функция является неопределенной.

Пример

Алгоритм решения задач с помощью данной таблицы крайне прост. К примеру, нам необходимо найти значение косинуса 30°. Для этого найдем ячейку пересечения строки косинуса и столбца значений для 30°. В данной ячейке находится искомое значение.

Таблица косинусов для 0°-180°

cos(1°)	0.9998
cos(2°)	0.9994
cos(3°)	0.9986
cos(4°)	0.9976
cos(5°)	0.9962
cos(6°)	0.9945
cos(7°)	0.9925
cos(8°)	0.9903
cos(9°)	0.9877
cos(10°)	0.9848
cos(11°)	0.9816
cos(12°)	0.9781
cos(13°)	0.9744
cos(14°)	0.9703
cos(15°)	0.9659
cos(16°)	0.9613
cos(17°)	0.9563
cos(18°)	0.9511
cos(19°)	0.9455
cos(20°)	0.9397
cos(21°)	0.9336
cos(22°)	0.9272
cos(23°)	0.9205
cos(24°)	0.9135
cos(25°)	0.9063
cos(26°)	0.8988
cos(27°)	0.891
cos(28°)	0.8829
cos(29°)	0.8746
cos(30°)	0.866
cos(31°)	0.8572
cos(32°)	0.848
cos(33°)	0.8387
cos(34°)	0.829
cos(35°)	0.8192
cos(36°)	0.809
cos(37°)	0.7986
cos(38°)	0.788
cos(39°)	0.7771
cos(40°)	0.766
cos(41°)	0.7547
cos(42°)	0.7431
cos(43°)	0.7314
cos(44°)	0.7193
cos(45°)	0.7071
cos(46°)	0.6947
cos(47°)	0.682
cos(48°)	0.6691
cos(49°)	0.6561
cos(50°)	0.6428
cos(51°)	0.6293
cos(52°)	0.6157
cos(53°)	0.6018
cos(54°)	0.5878
cos(55°)	0.5736
cos(56°)	0.5592
cos(57°)	0.5446
cos(58°)	0.5299
cos(59°)	0.515
cos(60°)	0.5

cos(61°)	0.4848
cos(62°)	0.4695
cos(63°)	0.454
cos(64°)	0.4384
cos(65°)	0.4226
cos(66°)	0.4067
cos(67°)	0.3907
cos(68°)	0.3746
cos(69°)	0.3584
cos(70°)	0.342
cos(71°)	0.3256
cos(72°)	0.309
cos(73°)	0.2924
cos(74°)	0.2756
cos(75°)	0.2588
cos(76°)	0.2419
cos(77°)	0.225
cos(78°)	0.2079
cos(79°)	0.1908
cos(80°)	0.1736
cos(81°)	0.1564
cos(82°)	0.1392
cos(83°)	0.1219
cos(84°)	0.1045
cos(85°)	0.0872
cos(86°)	0.0698
cos(87°)	0.0523
cos(88°)	0.0349
cos(89°)	0.0175
cos(90°)
cos(91°)	-0.0175
cos(92°)	-0.0349
cos(93°)	-0.0523
cos(94°)	-0.0698
cos(95°)	-0.0872
cos(96°)	-0.1045
cos(97°)	-0.1219
cos(98°)	-0.1392
cos(99°)	-0.1564
cos(100°)	-0.1736
cos(101°)	-0.1908
cos(102°)	-0.2079
cos(103°)	-0.225
cos(104°)	-0.2419
cos(105°)	-0.2588
cos(106°)	-0.2756
cos(107°)	-0.2924
cos(108°)	-0.309
cos(109°)	-0.3256
cos(110°)	-0.342
cos(111°)	-0.3584
cos(112°)	-0.3746
cos(113°)	-0.3907
cos(114°)	-0.4067
cos(115°)	-0.4226
cos(116°)	-0.4384
cos(117°)	-0.454
cos(118°)	-0.4695
cos(119°)	-0.4848
cos(120°)	-0.5

cos(121°)	-0.515
cos(122°)	-0.5299
cos(123°)	-0.5446
cos(124°)	-0.5592
cos(125°)	-0.5736
cos(126°)	-0.5878
cos(127°)	-0.6018
cos(128°)	-0.6157
cos(129°)	-0.6293
cos(130°)	-0.6428
cos(131°)	-0.6561
cos(132°)	-0.6691
cos(133°)	-0.682
cos(134°)	-0.6947
cos(135°)	-0.7071
cos(136°)	-0.7193
cos(137°)	-0.7314
cos(138°)	-0.7431
cos(139°)	-0.7547
cos(140°)	-0.766
cos(141°)	-0.7771
cos(142°)	-0.788
cos(143°)	-0.7986
cos(144°)	-0.809
cos(145°)	-0.8192
cos(146°)	-0.829
cos(147°)	-0.8387
cos(148°)	-0.848
cos(149°)	-0.8572
cos(150°)	-0.866
cos(151°)	-0.8746
cos(152°)	-0.8829
cos(153°)	-0.891
cos(154°)	-0.8988
cos(155°)	-0.9063
cos(156°)	-0.9135
cos(157°)	-0.9205
cos(158°)	-0.9272
cos(159°)	-0.9336
cos(160°)	-0.9397
cos(161°)	-0.9455
cos(162°)	-0.9511
cos(163°)	-0.9563
cos(164°)	-0.9613
cos(165°)	-0.9659
cos(166°)	-0.9703
cos(167°)	-0.9744
cos(168°)	-0.9781
cos(169°)	-0.9816
cos(170°)	-0.9848
cos(171°)	-0.9877
cos(172°)	-0.9903
cos(173°)	-0.9925
cos(174°)	-0.9945
cos(175°)	-0.9962
cos(176°)	-0.9976
cos(177°)	-0.9986
cos(178°)	-0.9994
cos(179°)	-0.9998
cos(180°)	-1

Таблица основных тригонометрических функций для углов 0, 30, 45, 60, 90, … градусов

Из тригонометрических определений функций $\sin$, $\cos$, $\tan$ и $\cot$ можно узнать их значения для углов $0$ и $90$ градусов:

$\sin⁡0°=0$, $\cos0°=1$, $\tan 0°=0$, $\cot 0°$ не определяется;

$\sin90°=1$, $\cos90°=0$, $\cot90°=0$, $\tan 90°$ не определяется.

В школьном курсе геометрии при изучении прямоугольных треугольников находят тригонометрические функции углов $0°$, $30°$, $45°$, $60°$ и $90°$.

Найденные значения тригонометрических функций для указанных углов в градусах и радианах соответственно ($0$, $\frac{\pi}{6}$, $\frac{\pi}{4}$, $\frac{\pi}{3}$, $\frac{\pi}{2}$) для удобства запоминания и использования заносят в таблицу, которую называют тригонометрической таблицей, таблицей основных значений тригонометрических функций и т.п.

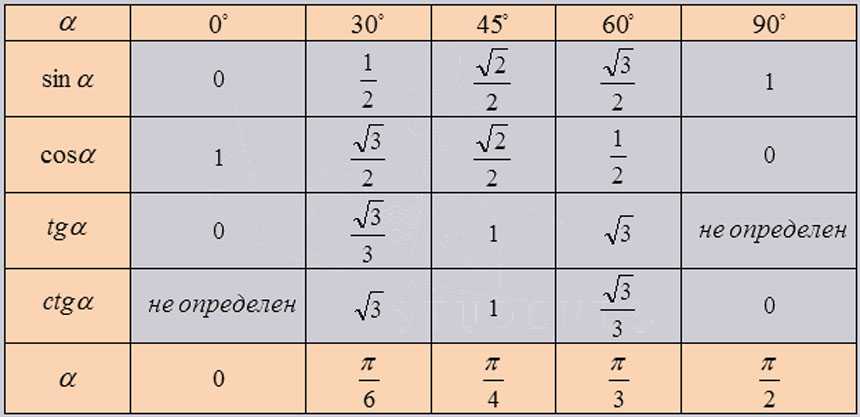
При использовании формул приведения, тригонометрическая таблица может быть расширена до угла $360°$ и соответственно $2\pi$ радиан:

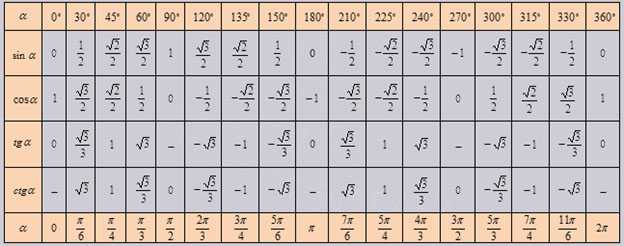
Применяя свойства периодичности тригонометрических функций, каждый угол, который будет отличаться от уже известного на $360°$, можно рассчитать и записать в таблицу. Например, тригонометрическая функция для угла $0°$ будет иметь такое же значение и для угла $0°+360°$, и для угла $0°+2 \cdot 360°$, и для угла $0°+3 \cdot 360°$ и т.д.

С помощью тригонометрической таблицы можно определить значения всех углов единичной окружности.

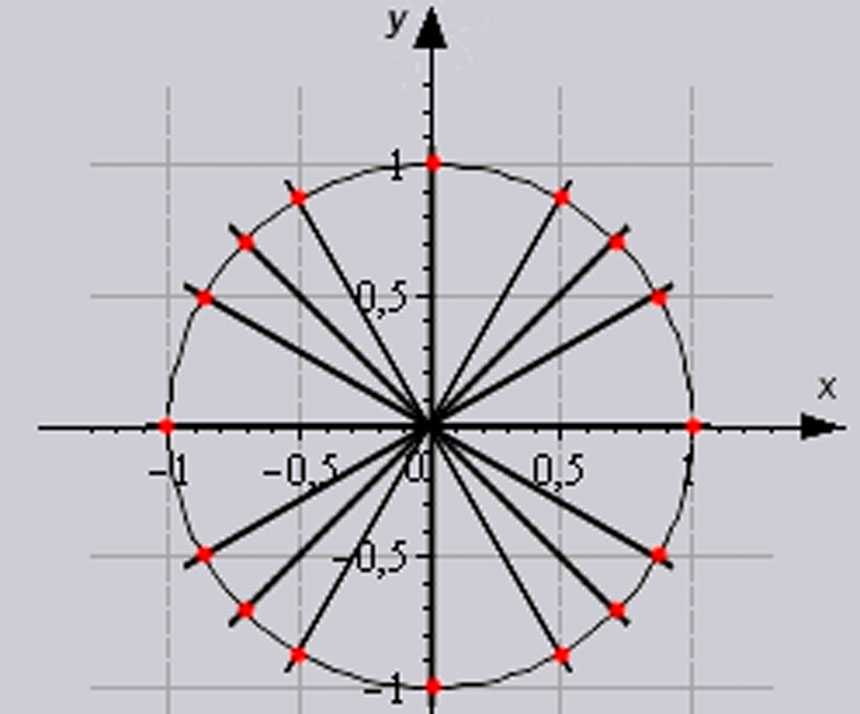
В школьном курсе геометрии предполагается запоминание основных значений тригонометрических функций, собранных в тригонометрической таблице, для удобства решения тригонометрических задач.

Практические примеры использования таблицы

Таблицам Брадиса легко можно найти применение в современном учебном процессе, например, выполняя школьные уроки.

Задача №1

10-метровая лестница опирается на здание таким образом, что имеет угол наклона 35°. Необходимо узнать расстояние от земли до ее вершины.

Решение

Имеем треугольник, где угол BСA = 90°, BАC = 30°. По определению^

sin ВАС = ВС /АВ

где ВС — высота лестницы, которую нужно найти, а АВ — известная из условия длина.

Таким образом:

$ВС\;=\;АВ\;х\;\sin\;ВАС$.

Узнав из таблицы Брадиса нужный синус и подставив все известные значения в формулу, можно найти ответ:

ВС (высота лестницы) = 10 м х 0,5736 = 5,736 метров.

Задача №2

Найдете длину тени от маяка высокой 30 м, если солнце находится в 60° над горизонтом.

Решение

Схематически условия задачи можно представить в виде треугольника, с прямым углом ВСА, и ВАС = 55°. По определению:

$ tg\;ВАС\;=\;АВ\;/\;СВ$

где АВ — высота маяка, а СВ — длина тени.

Отсюда $СВ\;=\;АВ\;/\;tg\;ВАС$.

Определив по таблице Брадиса нужную величину и подставив в формулу все известные значения, получим:

Использование таблицы

В таблице достаточно найти необходимую тригонометрическую функцию и значение угла или радиан, для которых эту функцию нужно вычислить. На пересечении строки с функцией и столбца со значением получим искомое значение тригонометрической функции заданного аргумента.

На рисунке можно увидеть, как найти значение $\cos⁡60°$, которое равно $\frac{1}{2}$.

Аналогично используется расширенная тригонометрическая таблица. Преимуществом ее использования является, как уже упоминалось, вычисление тригонометрической функции практически любого угла. Например, легко можно найти значение $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300°$:

Таблица синусов и косинусов

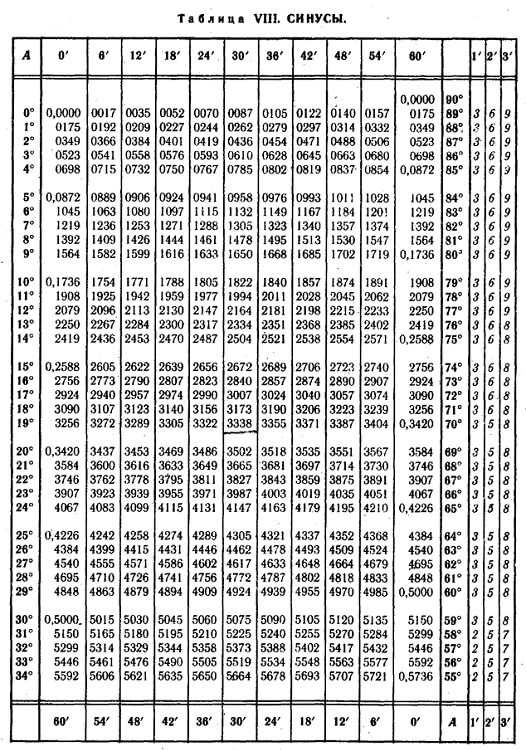
В силу широкого использования синусов и косинусов в учебных задачах, это самая распространенная из таблиц Брадиса. Она дает значение этих тригонометрических функций для любого острого угла от 0° до 90°. С помощью дополнительных колонок можно находить и более точные спецификации. Это 6′, 12′,18, 24′, 30′, 36′, 42′, 48′ и 54′ для углов указанного диапазона, например:

$\sin\;10^\circ\;=\;0,1736$. С помощью дополнительных колонок находим — $\sin\;10^\circ\;12’\;=\;0,1771,\;\sin\;10^\circ\;24’\;=\;0,1805$;
$\sin\;50^\circ\;=\;0,7660$. Обращаясь к дополнительной колонке выясняем, что $\sin\;50^\circ\;12’\;=\;0,7683,\;\sin\;50^\circ\;24’\;=\;0,7705$.

Если нужны еще более точные показатели, то нужно использовать поправочные коэффициенты, отнимая и прибавляя их к ближайшему табличному значению минут. Используя их, находим:

$\sin\;10^\circ\;15’\;=\;\sin\;10^\circ\;12’\;+\;0,0009\;=\;0,1771+0,0009\;=\;0,1780$;
$\sin\;50^\circ\;22’\;=\;\sin\;50^\circ\;24′-0,0004\;=\;0,7705-0,0004\;=\;0,7701$.

Для нахождения косинусов можно использовать значения в правой колонке, но куда удобнее вычислять через синус угла, дополняющего до 90°. В этом случае:

$\cos\;10^\circ\;=\;\sin\;80^\circ\;=\;0,9848;$
$\cos\;50^\circ\;=\;\sin\;40^\circ\;=\;0,6428.$

Аналогично проводят и более точные вычисления, в том числе — с использованием поправочных коэффициентов:

$\cos\;10^\circ\;12’\;=\;\sin\;79^\circ\;48’\;=\;0,9842;$
$\cos\;10^\circ\;15’\;=\;\sin\;79^\circ\;45’\;=\;\sin\;79^\circ\;48′-0,0002\;=\;0,9842-0,002\;=\;0,9840;$
$\cos\;50^\circ\;24’\;=\;\sin\;39^\circ\;36’\;=\;0,6374;$
$\cos\;50^\circ\;22’\;=\;\sin\;39^\circ\;38’\;=\;\sin\;39^\circ\;36’\;+\;0,0004\;=0,6374\;+\;0,0004\;=\;0,6380.$