Как посчитать среднее арифметическое
Чтобы посчитать среднее арифметическое, нужно сложить все имеющиеся значения какой-либо величины и разделить на количество этих значений. Для четырёх значений $a, b, c, d$ среднее арифметическое равно
$\frac{a+b+c+d}{4}$.
Если же $a, b, c$ и $d$ заданы не в одной единице измерения, а, например, в метрах и сантиметрах, то сначала нужно выбрать общую единицу измерения и привести все значения к ней.
Пример 1
Эдуард прыгнул в длину $5$ раз. Первый раз он прыгнул на расстояние $173$ см, второй раз на $169$ см, третий раз на $1,7$ м, а четвёртый и пятый соответственно — на $168$ и $175$ см. Посчитайте, на какую длину в среднем прыгает Эдуард.
Решение:
Длина третьего прыжка Эдуарда дана в метрах, а остальные его результаты — в сантиметрах. Поэтому переведём длину третьего результата также в сантиметры. Для этого умножим метры на $100$, так как в одном метре содержится 100 сантиметров:
$l_3=1,7 м = 1,7 \cdot 100 см= 170$ см.
Теперь мы можем найти среднюю длину его прыжка:
$l_{ср.}=\frac{173+169+170+168+175}{5}=171$ см.
Ответ: В среднем Эдуард прыгает на длину в 171 см.
Средне-арифметическое – что это значит?
Не только в различных математических науках, но и в повседневной жизни возникают случаи, когда нужно рассчитать средний показатель чего-либо. Например, среднюю стоимость огурцов на рынке, средний рост ребенка, среднюю стоимость проживания в гостинице и пр.
Всему этому уже давно было придумано научное название – «среднее арифметическое». Данный показатель активно применяется в статистике для обобщения результатов. К примеру, средний возраст для рождения детей, средний возраст смерти среди мужчин и женщин, средняя заработная плата по регионам и по России в целом.
К примеру, при принятии закона о повышении пенсионного возраста, власти как раз исходили из среднего возраста смерти в нашей стране.
Разберемся, что же представляет собой данный показатель.
К примеру, в 2017 году полное среднее образование получили дети разных возрастов : 16, 17 и 18 лет. Среднее арифметическое будет рассчитано, как сумма всех возрастов, деленная на три. Итого средний возраст ребёнка, окончившего 11 класс, составил 17 лет.
В данном примере показан примитивный расчет на примере трех детей. По факту суммировать нужно все данные, имеющиеся в наличии. То есть если речь будет идти о пяти детях, то мы суммируем их возраст, к примеру, 17+17+18+16+17 и делим полученное на пять.
То есть в общем виде формулу можно представить так:
Среднее арифметическое = (сумма всех имеющихся значений)/общее число значений, что участвуют в операции.
Таким образом, расчет довольно прост, даже для школьников
Затруднения могут возникнуть лишь по причине большого количества респондентов, участвующих в операции.
Важно понимать, что средний показатель не является просто числом. Он имеет особый физический смысл, который уже долгие годы применяется в реальном мире на практике.
Средних, на самом деле, существует несколько
Однако в каждом случае, только одно из них верное. В каждой из операций, нужно использовать только тот вид среднего, который необходим, иначе будет допущена огромная ошибка.
Какие виды средних используются на практике? Самые распространенные средние – это:
Среднее арифметическое;
Среднее геометрическое;
Среднее гармоническое.
Эти значения наиболее часто используются, как в повседневной жизни, так и в науках. Наиболее часто, конечно же, рассчитывается первый показатель.
Зачастую данный показатель в реальных условиях применяется и рассчитывается неверно. Почему так происходит? Фактически, базой среднего арифметического выступает применение закона о больших числах. Кроме того, применяется и допущение, согласно которому исходная величина является нормально определенной.
Это означает, что вокруг представленного в ряде значений, имеется наиболее частое отклонение в какую-либо сторону. То есть. В большую или меньшую. Например, в ряду чисел 8,8,9,8,9,8,8, отклонение будет в меньшую сторону, так как больше восьмерок. А в ряде: 17,17, 20,20,20,20,20, отклонение, наоборот, будет в большую сторону, так как в этом случае больше все же «двадцаток».
Однако в большинстве случаев, такие отклонения являются небольшими и обычно равными по вероятности. Суть проблемы в том, что в бизнесе, как и в реальной жизни, нормальность распределения на практике можно встретить крайне редко.
На практике нормальность распределения часто можно встретить при наличии большого количества значений, начиная с сотен и тысяч. К примеру, количество обращений в техническую поддержку крупной компании может быть распределено нормально, как на бумаге, так и фактически.
Тем не менее, только лишь количества не будет достаточно, ведь в каждой конкретной ситуации нужно следить и за правильностью распределения. Только так можно будет правильно в итоге рассчитать значение среднего арифметического.
Средняя арифметическая взвешенная
Рассмотрим следующую простую задачу. Между пунктами А и Б расстояние S, которые автомобиль проехал со скоростью 50 км/ч. В обратную сторону – со скоростью 100 км/ч.
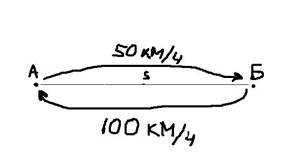
Какова была средняя скорость движения из А в Б и обратно? Большинство людей ответят 75 км/ч (среднее из 50 и 100) и это неправильный ответ. Средняя скорость – это все пройденное расстояние, деленное на все потраченное время. В нашем случае все расстояние – это S + S = 2*S (туда и обратно), все время складывается из времени из А в Б и из Б в А. Зная скорость и расстояние, время найти элементарно. Исходная формула для нахождения средней скорости имеет вид:
Теперь преобразуем формулу до удобного вида.
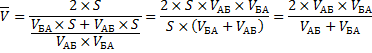
Подставим значения.
Правильный ответ: средняя скорость автомобиля составила 66,7 км/ч.
Средняя скорость – это на самом деле среднее расстояние в единицу времени. Поэтому для расчета средней скорости (среднего расстояния в единицу времени) используется средняя арифметическая взвешенная по следующей формуле.
где x – анализируемый показатель; f – вес.
Аналогичным образом по формуле средневзвешенной средней рассчитывается средняя цена (средняя стоимость на единицу продукции), средний процент и т.д. То есть если средняя считается по другим усредненным значениям, нужно применить среднюю взвешенную, а не простую.
Выборка. Объем. Размах
Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней
Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6
n = 6
Элементы выборки обозначаются с помощью переменных с индексами . Последний элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.
Обозначим элементы нашей выборки через переменные
Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.
Размахом выборки называют разницу между самым большим и маленьким элементом выборки.
В нашем случае, самым большим элементом выборки является элемент 250, а самым маленьким — элемент 150. Разница между ними равна 100
Формула средневзвешенного значение в Excel
Обычная функция среднего значения в Excel СРЗНАЧ, к сожалению, считает только среднюю простую. Готовой формулы для среднего взвешенного значения в Excel нет. Однако расчет несложно сделать подручными средствами.
Самый понятный вариант создать дополнительный столбец. Выглядит примерно так.
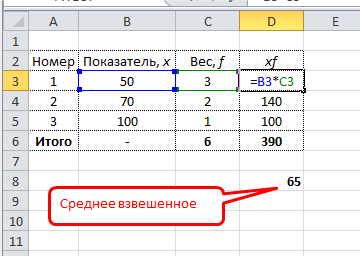
Имеется возможность сократить количество расчетов. Есть функция СУММПРОИЗВ. С ее помощью можно рассчитать числитель одним действием. Разделить на сумму весов можно в этой же ячейке. Вся формула для расчета среднего взвешенного значения в Excel выглядит так:
=СУММПРОИЗВ(B3:B5;C3:C5)/СУММ(C3:C5)
Интерпретация средней взвешенной такая же, как и у средней простой. Средняя простая – это частный случай взвешенной, когда все веса равны 1.
Натуральные и десятичные дроби
Если массив чисел представлен десятичными дробями, решение происходит по способу вычисления среднего арифметического целых чисел, но сокращение итога производится по требованиям задачи к точности результата.При работе с естественными дробями их следует привести к всеобщему знаменателю, тот, что умножается на число чисел в массиве. В числителе результата будет сумма приведенных числителей начальных дробных элементов.
Совет 5: Как обнаружить среднее геометрическое чисел
Среднее геометрическое чисел зависит не только от безусловной величины самих чисел, но и от их числа. Невозможно путать среднее геометрическое и среднее арифметическое чисел, от того что они находятся по различным методологиям. При этом среднее геометрическое неизменно поменьше либо равно среднему арифметическому.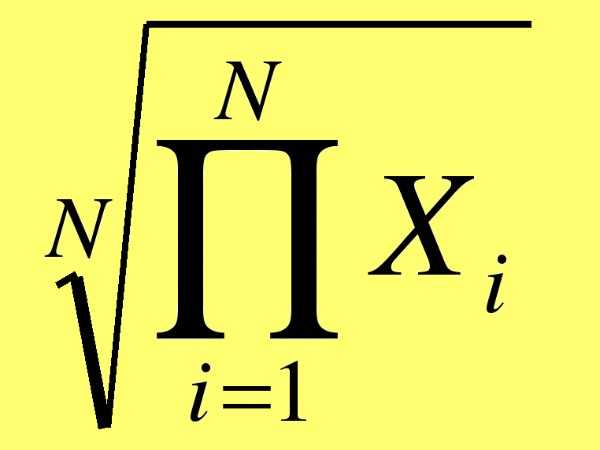
Вам понадобится
Инженерный калькулятор.
Инструкция
1. Рассматривайте, что в всеобщем случае среднее геометрическое чисел находится путем перемножения этих чисел и извлечения из них корня степени, которая соответствует числу чисел. Скажем, если надобно обнаружить среднее геометрическое пяти чисел, то из произведения необходимо будет извлекать корень пятой степени.2. Для нахождения среднего геометрического 2-х чисел используйте основное правило. Обнаружьте их произведение, позже чего извлеките из него квадратный корень, от того что числа два, что соответствует степени корня. Скажем, для того дабы обнаружить среднее геометрическое чисел 16 и 4, обнаружьте их произведение 16•4=64. Из получившегося числа извлеките квадратный корень ?64=8. Это и будет желанная величина
Обратите внимание на то, что среднее арифметическое этих 2-х чисел огромнее и равно 10. Если корень не извлекается нацело, произведите округление итога до надобного порядка.3
Дабы обнаружить среднее геометрическое больше чем 2-х чисел, тоже используйте основное правило. Для этого обнаружьте произведение всех чисел, для которых надобно обнаружить среднее геометрическое. Из полученного произведения извлеките корень степени, равной числу чисел. Скажем, дабы обнаружить среднее геометрическое чисел 2, 4 и 64, обнаружьте их произведение. 2•4•64=512. От того что необходимо обнаружить итог среднего геометрического 3 чисел, что из произведения извлеките корень третей степени. Сделать это устно затруднительно, следственно воспользуйтесь инженерным калькулятором. Для этого в нем есть кнопка “x^y”. Наберите число 512, нажмите кнопку “x^y”, позже чего наберите число 3 и нажмите кнопку “1/х”, дабы обнаружить значение 1/3, нажмите кнопку “=”. Получим итог возведения 512 в степень 1/3, что соответствует корню третьей степени. Получите 512^1/3=8. Это и есть среднее геометрическое чисел 2,4 и 64.4. С поддержкой инженерного калькулятора дозволено обнаружить среднее геометрическое иным методом. Обнаружьте на клавиатуре кнопку log. Позже этого возьмите логарифм для всего из чисел, обнаружьте их сумму и поделите ее на число чисел. Из полученного числа возьмите антилогарифм. Это и будет среднее геометрическое чисел. Скажем, для того дабы обнаружить среднее геометрическое тех же чисел 2, 4 и 64, сделайте на калькуляторе комплект операций. Наберите число 2, позже чего нажмите кнопку log, нажмите кнопку “+”, наберите число 4 и вновь нажмите log и “+”, наберите 64, нажмите log и “=”. Итогом будет число, равное сумме десятичных логарифмов чисел 2, 4 и 64. Полученное число поделите на 3, от того что это число чисел, по которым ищется среднее геометрическое. Из итога возьмите антилогарифм, переключив кнопку регистра, и используйте ту же клавишу log. В итоге получится число 8, это и есть желанное среднее геометрическое.Обратите внимание!
Среднее значение не может быть огромнее самого большого числа в комплекте и поменьше самого маленького.Полезный совет
В математической статистике среднее значение величины именуется математическим ожиданием.
Среднее арифметическое число в 6 классе
Среднее арифметическое число является одним из основных понятий в математике. Этот термин широко используется в школьной программе для обучения учащихся.
Среднее арифметическое число получается путем нахождения суммы всех чисел и деления этой суммы на их количество. Другими словами, среднее арифметическое число представляет собой средний результат численного ряда.
Для вычисления среднего арифметического числа, вам нужно сложить все числа в данной последовательности и разделить полученную сумму на их количество.
Например, если у вас есть последовательность чисел: 2, 4, 6, 8, 10, среднее арифметическое число будет:
- Сложить все числа: 2 + 4 + 6 + 8 + 10 = 30.
- Количество чисел в последовательности равно 5.
- Разделить сумму на количество: 30 / 5 = 6.
Таким образом, среднее арифметическое число для данной последовательности равно 6.
Среднее арифметическое число имеет несколько свойств. Одно из них — прибавление или вычитание одной и той же величины к каждому числу в последовательности не изменяет его среднего арифметического числа. Кроме того, если все числа в последовательности умножаются или делятся на одно и то же число, среднее арифметическое число также умножается или делится на это число.
Среднее арифметическое число может использоваться для решения различных задач, например, для определения средней оценки по предмету или среднего времени выполнения задания.
Важно помнить, что среднее арифметическое число не всегда является представителем реальных данных. Например, если ученики всех оценок получают пятерки, среднее арифметическое число по этой оценке будет пять, но это не отразит реальной ситуации в группе учащихся
В заключение, среднее арифметическое число — это удобное математическое понятие, которое позволяет нам суммировать и анализировать большие наборы чисел и получать общую характеристику этой последовательности.
Определение среднего геометрического
Среднее геометрическое чисел — это корень произведения этих чисел, показатель которого равен числу этих чисел.
Средняя гармоническая
Определяющей характеристикой гармонического среднего является то, что при усреднении сумма обратных средних остается неизменной.
Формула средневзвешенной геометрической используется в тех случаях, когда статистическая информация не содержит частот f для отдельных вариантов x совокупности и представлена в виде их произведения xf. Для вычисления среднего геометрического необходимо положить: xf = w, откуда f = w/x.
Преобразуем формулу для среднего арифметического так, чтобы доступные данные x и w можно было использовать для вычисления среднего. В формулу средневзвешенной арифметической вместо xn подставляем w, а вместо n — отношение w/x, и таким образом получаем формулу гармонической средневзвешенной:
Гармоническое простое среднее используется, когда вес каждой альтернативы равен единице. Он рассчитывается по формуле:
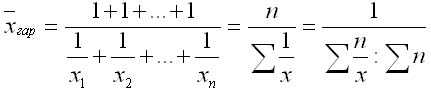
где 1/x — отдельные варианты обратного хода, встречающиеся один раз;
n — количество альтернатив.
Средняя квадратичная
Например, среднеквадратичное значение используется для расчета среднего размера сторон n квадратных сечений, среднего диаметра бревен, труб и т д. Оно делится на два вида.
Среднеквадратичное значение простое. Если при замене отдельных значений свойства средним значением необходимо оставить неизменной сумму квадратов исходных значений, то среднее будет квадратом среднего.
Это квадратный корень из частного суммы квадратов значений отдельных функций, деленного на число:
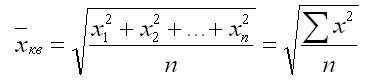
Средний квадратный вес рассчитывается по формуле:
где f — знак веса.
Средняя кубическая
Средняя кубическая используется, например, при определении средней длины стороны и кубов. Он делится на два типа.
Средний кубический простой:
Средний кубический вес:
Среднеквадратичное и среднекубическое не получили широкого распространения в практической статистике. Часто в статистике используют среднеквадратичное значение, но не от самих факторов x, а от их отклонения от среднего при расчете показателей вариации.
Среднее значение можно рассчитать не для всего, а для части данных о населении. Примером может служить прогрессивная средняя как одна из частных средних, рассчитанная не для всех, а только для «лучших» (например, для показателей выше или ниже индивидуальных средних).
Структурные средние
Для характеристики центрального тренда в статистических распределениях рационально наряду со средним арифметическим использовать определенное значение признака X, которое в силу определенных особенностей своего расположения в ряду распределения может характеризовать уровень.
Это особенно важно, когда крайние значения функции в ряду распределения имеют нечеткие границы. В связи с этим точное определение среднего арифметического обычно невозможно или весьма затруднено
В таких случаях средний уровень можно определить, взяв, например, значение функции, расположенное в середине частотного ряда или наиболее часто встречающееся в соответствующем ряду.
Такие значения зависят только от характера частот, т.е структуры распределения. Они типичны с точки зрения расположения в частотном ряду, поэтому такие значения считаются характеристиками распределительного центра и поэтому определены как структурные средние.
Они используются для изучения внутренней структуры и структуры рядов распределения значений признаков. К таким показателям относятся мода и медиана.
Мода и медиана очень часто вычисляются в статистических задачах, а также являются дополнительными характеристиками совокупности и используются в математической статистике для анализа типа ряда распределения, который может быть нормальным, асимметричным, симметричным и т д
Кроме медианы вычисляют значения признака, разделяя совокупность на четыре равные части — квартили, на пять частей — квинтили, на десять равных частей — децили, на сто равных частей — проценты. Использование распределения оцениваемых признаков в статистике при анализе вариационных рядов позволяет более глубоко и детально характеризовать изучаемую совокупность.
Интересные факты
- По статистике, дети улыбаются 400 раз в день, а взрослые всего 17. Улыбайтесь чаще!
- В России продолжительность жизни мужчин составляет 70 лет, женщин – 78 лет!
- Ежедневно в Росси рождается 5000 детей.
- Ученые подсчитали, за всю жизнь, человек тратит 5 лет на процесс приема пищи,
- Ученые подсчитали, за 70 лет, человек поглощает более 50000 килограммов пищи, в том числе около 200-300 килограммов поваренной соли. Так же, каждый человек, достигший 70 летнего возраста, выпил за всю жизнь 50000 литров воды, что больше в 1400 раз массы человеческого тела.
- Одной хорошей шариковой ручкой можно написать 50000 слов.
Когда трескается стекло, трещина распространяется со скоростью 5000 км/ч.
Урок по математике»Среднее арифметическое чисел»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. Урок по математике 5 класс (учебник Виленкина)
Урок по математике 5 класс (учебник Виленкина)
Дидактическая цель урока: познакомить с решением обратных задач, учить находить среднее арифметическое.
I. Организационный момент
1. Индивидуальная работа у доски
Задание 1. найдите среднее арифметическое чисел
18,3; 43,5; 32,1 (31,3)
Задание 2. найдите значение выражения
Задание 3. Решите уравнение
8х – 3,2 = 5,6 (х = 1.1)
2. Фронтальная работа (учащиеся работают вместе с учителем)
(Учитель показывает карточки с заданием, учащиеся называют ответ, возможно использование слайдов презентации)
(6.45 – 5,79) 0
7,59 0,1
3. Взаимопроверка в парах
4. Решите задачу
В киоске продаются три вида шоколадок и пять сортов мороженого. Сколькими разными способами можно купить шоколадку и мороженое?
— что это за задача? Докажите.
— Сколько различных вариантов мороженого можно выбрать для первой шоколадки? (5)
— Для второй? Третьей?
— Сколько же различных способов выбора существует? (3 5 = 15)
III. Определение темы урока
3.5; 3.7; 4,2 60; 65; 85 1.8; 2,5; 6,8
— Какое задание можно придумать для этих чисел?
(Учащиеся могут предложить разные варианты заданий для этих чисел, учитель выбирает для выполнения самые интересные, например найти среднее арифметическоедля этих чисел)
— Что такое среднее арифметическое?
— Сформулируйте тему урока.
IV. Работа по теме урока
1. Найти среднее арифметическое чисел
(3,5 + 3,7 + 4,2) : 3 = 3,8
(60 + 65 + 85) : 3 = 70
(1,8 + 2,5 + 6,8) : 3 = 3,7
— Расскажите, как найти среднее арифметическое нескольких чисел.
2. Найти среднее арифметическое чисел (работа в парах)
25,6; 28,7; 14,4; 12,8
32,7; 14,84; 15,3; 21,6
Проверка (взаимопроверка, работа в парах)
(25,6 + 28,7 + 14,4 + 12,8) : 4 = 20,375
(2,8 + 42,3 + 7,4 + 16,5) : 4 = 17,25
(32,7 + 14,84 + 15,3 + 21,6) : 4 = 21,1
— Подумайте, что следует из равенства отрезков АВ и ВС. (Координата точки В является средним арифметическим координат двух других точек)
— Чему равна координата точки С ? (10, 1)
4. Ответьте на вопросы.
— Как вычислить среднее арифметическое? (Среднее арифметическое = сумма слагаемых : количество слагаемых)
— Как найти сумму чисел? (сумма слагаемых = Среднее арифметическое количество слагаемых)
— Как найти количество слагаемых ? (количество слагаемых = сумма слагаемых : среднее арифметическое)
— Как можно назвать эти задачи по отношению друг к другу? (Обратные)
— Какая это задача?
— Можем ли мы найти сумму этих двух чисел, если известно среднее арифметическое?
— Как это сделать?
— Теперь можем ответить на вопрос задачи?
1) 3,1 2 = 6,2 – сумма двух чисел
2) 6,2 – 3,8 =2,4 – второе число
— Подумайте, можно ли решить эту задачу алгебраически?
— Что следует обозначить через х?
Тогда среднее арифметическое этих чисел будет (х + 3,8) : 2.
А по условию среднее арифметическое равно 3,1
Значит можем составить уравнение:
х + 3,8 = 3,1 2
х = 2,4 — второе число.
— Какой путь решения выберем? (Алгебраический)
— Что обозначим через х?
Пусть меньшее число будет х.
Тогда второе число будет 1,5 х.
Среднее арифметическое этих чисел (х + 1,5 х) : 2
А по условию среднее арифметическое равно 30.
Значит, можем состамить уравнение
2,5х = 30 2
х = 24 – меньшее из чисел
24 1,5 = 36 – второе число
VI . Повторение изученного материала
3,5х – 2.3х + 3,8 = 4.28 4,7у – (2,5у + 12,4) = 1,9
Ответ: 0,4 Ответ: 6,5
VII . Самостоятельная работа
1000 : 0,01 = 100 000
— Как найти сумму чисел, если известны среднее арифметическое и количество слагаемых?
— Как вы оцениваете себя на этом уроке?
— А как вы оцениваете своего товарища, который работал с вами в паре?
С.230, № 1528, 1532, 1534 (б).
Курс повышения квалификации
Сейчас обучается 945 человек из 80 регионов
Курс профессиональной переподготовки
Сейчас обучается 687 человек из 75 регионов
Курс повышения квалификации
Практическое применение среднего арифметического числа
Среднее арифметическое число является одним из основных понятий в математике, которое применяется повседневно в различных сферах жизни. Ниже приведены некоторые практические примеры использования среднего арифметического числа.
-
Оценка успеваемости
В школе среднее арифметическое число используется для оценки успеваемости учеников. Путем расчета среднего арифметического по различным предметам, можно получить представление о том, насколько хорошо ученик усваивает материал и какие предметы ему легче или сложнее. Это позволяет преподавателям и родителям принять меры по дополнительной поддержке и развитию учащихся.
-
Расчет среднего бюджета
В финансовой сфере среднее арифметическое число применяется для расчета среднего бюджета. Например, при планировании семейного бюджета или бюджета компании, можно узнать средние ежемесячные расходы по различным категориям. Эта информация помогает контролировать расходы и принимать решения о необходимости сокращения или перераспределения финансовых ресурсов.
-
Статистический анализ данных
В научной и статистической сферах среднее арифметическое число используется для анализа данных. Например, при исследовании определенного явления или проведении опросов, среднее арифметическое помогает получить среднее значение ответов или результатов. Это позволяет сделать выводы о распределении данных и оценить общую характеристику явления.
-
Определение средней температуры
В метеорологии среднее арифметическое число используется для определения средней температуры за определенный период времени. Путем сбора и анализа данных с различных метеостанций можно установить среднюю температуру за год, месяц или день. Это помогает прогнозировать климатические изменения и принимать меры по адаптации к ним.
Как видно из приведенных примеров, среднее арифметическое число играет важную роль в различных областях жизни. Оно помогает систематизировать и анализировать данные, получать представление о различных явлениях, а также принимать взвешенные решения на основе этих данных.
Задачи на нахождение среднего арифметического натуральных чисел
Автомобиль $2$ часа ехал через город со скоростью $30$ км/ч, по пригороду час со скоростью $60$ км/час, а затем ещё $3$ часа по трассе со скоростью $100$ км/час. Вычислите среднюю скорость автомобиля.
Сначала найдём сумму всех расстояний. У нас получится $30 \cdot 2 + 60 + 100 \cdot 3 = 420$
Теперь разделим эту сумму расстояний на количество часов.
$$420 : 6 = 70$$
Следовательно, если бы автомобиль ехал со скоростью $70$ км/ч в течение такого же времени ($6$ часов), он проехал бы такое же расстояние.
Рассмотрим другую задачу.
Первый рабочий за рабочий день собирает $50$ деталей, второй – $44$ более сложные детали, а третий работает над самыми сложными и делает за день гораздо меньше деталей. Сколько деталей он делает, учитывая, что средняя производительность всех трёх рабочих $38$ деталей за смену?
Зная, что средняя производительность $38$, а рабочих трое, мы можем найти сумму деталей, которые они собирают за день.
$$38 \cdot 3 = 114$$
Теперь просто вычтем из этого числа то, что делают первые двое рабочих и найдём количество деталей, которые делает третий.
$$114-50-44 = 20$$
Показать проверку
Скрыть
$$(50 + 44 + 20) : 3 = 114 : 3 = 38$$
{"questions":[{"content":"$23$ ученика писали контрольную работу. Пятеро написали на «$5$», тринадцать – на «$4$», остальные на «$3$». Каков средний балл по классу?`input-1`","widgets":{"input-1":{"type":"input","answer":"4"}},"step":1,"hints":["Сначала найдём число учеников, написавших работу на «$3$». Это нужно нам для нахождения суммы всех баллов. <br />$23-18 = 5$","Теперь вычисляем сумму баллов. Для этого каждую отметку умножаем на количество детей, которые её получили. <br />$5 \\cdot 5 + 4 \\cdot 13 + 3 \\cdot 5 = 25 + 52 + 15 = 92$","Теперь нужно полученную сумму разделить на количество учеников. Это и будет средний балл.<br />$92 : 23 = 4$"]}]}
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров
Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат
Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:
Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:
Выпишем рост спортсменов отдельно:
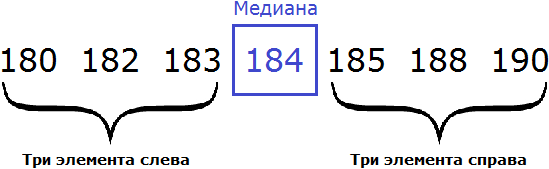
180, 182, 183, 184, 185, 188, 190
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:
Построим этих шестерых спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186
Найдем среднее арифметическое элементов 184 и 186
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Общие сведения
Понятие среднеарифметической величины впервые предложил древнегреческий ученый — Пифагор. Позднее этот термин стал использоваться в математике. Чтобы понять его смысл, необходимо получить базовые знания о числовых значениях. Они делятся на 2 вида:
- Целые.
- Дробные.
Первый тип — натуральные числа, они применяются при устном счете предметов.
Дробные бывают также двух типов:
- Десятичными.
- Обыкновенными.
Десятичные дроби делятся на конечные, периодические и непериодические бесконечные. Первый тип состоит из целой и дробной частей, разделенных между собой запятыми. Как правило, количество разрядов ограничено определенным значением. Если рассматривать бесконечные периодические десятичные дробные выражения, они состоят из множества элементов. Последние повторяются с определенной периодичностью. Например, 5,(321), где величина периода указывается в круглых скобках.
В случае когда дробное тождество является бесконечным непериодическим, очень часто представление осуществляется в форме обыкновенной дроби. Последняя состоит из делимого и делителя, отделенных друг от друга косой чертой «/». Первый элемент именуется числителем, а второй — знаменателем.
Обыкновенные дробные выражения бывают правильными, неправильными, а также могут записываться в форме смешанного числа, т. е. величины, состоящей из целого компонента и обыкновенной правильной дроби.