Треугольник определение обозначение виды

Равнобедренный треугольник: свойства, признаки и формулы

1. Свойства равнобедренного треугольника.
2. Признаки равнобедренного треугольника.
3. Формулы равнобедренного треугольника:
   • формулы длины стороны;
   • формулы длины равных сторон;
   • формулы высоты, медианы, биссектрисы равнобедренного треугольника.

Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.

АВ = ВС — боковые стороны

АС — основание

Свойства равнобедренного треугольника

Свойства равнобедренного треугольника выражаются через 5 теорем:

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Доказательство теоремы:

Рассмотрим равнобедренный Δ ABC с основанием АС.

Боковые стороны равны АВ = ВС,

Следовательно углы при основании ∠ BАC = ∠ BСA.

• Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
• Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
• Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Доказательство теоремы:

• Дан Δ ABC.
• Из точки В проведем высоту BD.
• Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.к. гипотенузы и общий катет у них равны (теорема Пифагора).
• Прямые АС и BD называются перпендикуляром.
• В Δ ABD и Δ BCD∠ BАD = ∠ BСD (из Теоремы 1).
• АВ = ВС — боковые стороны равны.
• Стороны АD = СD, т.к. точка D отрезок делит пополам.
• Следовательно Δ ABD = ΔBCD.
• Биссектриса, высота и медиана это один отрезок – BD

Вывод:

1. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
2. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
3. Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.

Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.

Теорема 5. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство теоремы:

Дано два Δ ABC и Δ A1B1C1. Стороны AB = A1B1; BC = B1C1; AC = A1C1.

Доказательство от противного.

• Пусть треугольники не равны (а то треугольники были равны по первому признаку).
• Пусть Δ A1B1C2 = Δ ABC, у которого вершина C2 лежит в одной полуплоскости с вершиной C1 относительно прямой A1B1. По предположению вершины C1 и C2 не совпадают. Пусть D – середина отрезка C1C2. Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую.
• Отсюда пришли к противоречию и теорему доказали.

Признаки равнобедренного треугольника

1. Если в треугольнике два угла равны.
2. Сумма углов треугольника 180°.
3. Если в треугольнике биссектриса является медианой или высотой.
4. Если в треугольнике медиана является биссектрисой или высотой.
5. Если в треугольнике высота является медианой или биссектрисой.

Формулы сторон равнобедренного треугольника

• b — сторона (основание)
• а — равные стороны
• a — углы при основании
• b — угол образованный равными сторонами

Формулы длины стороны (основания — b):

• b = 2a \sin( \beta /2)= a \sqrt { 2-2 \cos \beta }
• b = 2a \cos \alpha

Формулы длины равных сторон — (а):

• a=\frac { b } { 2 \sin(\beta /2) } = \frac { b } { \sqrt { 2-2 \cos \beta } }
• a=\frac { b } { 2 \cos\alpha }

Формулы высоты, медианы, биссектрисы равнобедренного треугольника

• L — высота=биссектриса=медиана
• b — сторона (основание)
• а — равные стороны
• a — углы при основании
• b — угол образованный равными сторонами

Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):

• L = a sina
• L = \frac { b } { 2 } *\tg\alpha
• L = a \sqrt { (1 + \cos \beta)/2 } =a \cos (\beta)/2)

Формула высоты, биссектрисы и медианы, через стороны, (L):

L = \sqrt { a { 2 } -b { 2 } /4 }

Площадь равнобедренного треугольника

• b — сторона (основание)
• а — равные стороны
• h — высота

Формула площади треугольника через высоту h и основание b, (S):

S=\frac { 1 } { 2 } *bh

Смотри также:

Что такое треугольник: определение, классификация, свойства

В данной публикации мы рассмотрим определение, классификацию и свойства одной из основных геометрических фигур – треугольника. Также разберем примеры решения задач для закрепления представленного материала.

• Определение треугольника
• Классификация треугольников
• Свойства треугольника
• Примеры задач

Определение треугольника

Треугольник – это геометрическая фигура на плоскости, состоящая из трех сторон, которые образованы путем соединения трех точек, не лежащих на одной прямой. Для обозначения используется специальный символ – △.

• Точки A, B и C – вершины треугольника.
• Отрезки AB, BC и AC – стороны треугольника, которые часто обозначаются в виде одной латинской буквы. Например, AB = a, BC = b, AC = c.
• Внутренность треугольника – часть плоскости, ограниченная сторонами треугольника.

Стороны треугольника в вершинах образуют три угла, традиционно обозначающиеся греческими буквами – α, β, γ и т.д. Из-за этого треугольник еще называют многоугольником с тремя углами.

Углы можно, также, обозначать с помощью специального знака “∠“:

• α – ∠BAC или ∠CAB
• β – ∠ABC или ∠CBA
• γ – ∠ACB или ∠BCA

Классификация треугольников

В зависимости от величины углов или количества равных сторон выделяют следующие виды фигуры:

1. Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°.

2. Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

3. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°.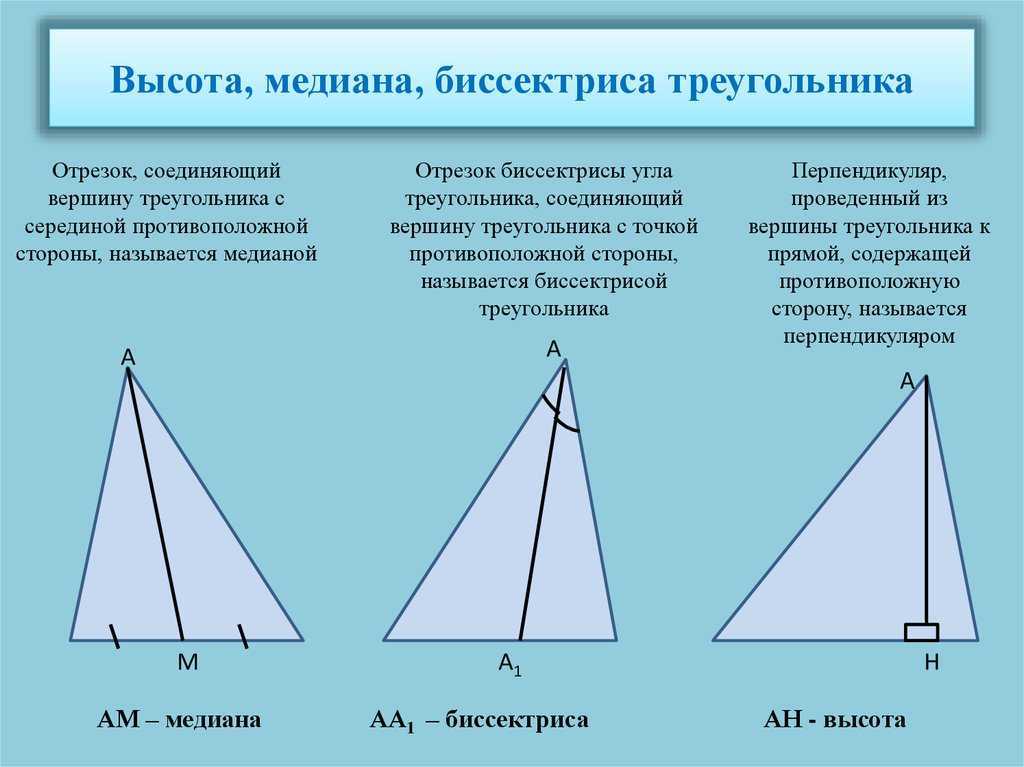

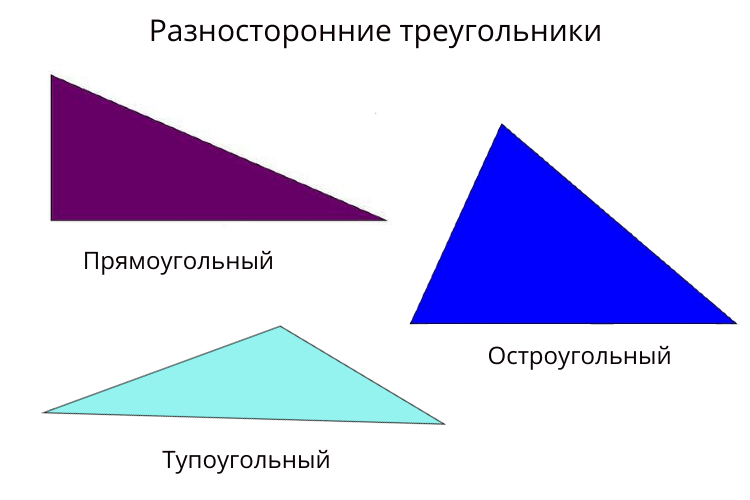
4. Разносторонний – треугольник, у которого все стороны имеют разную длину.

5. Равнобедренный – треугольник, имеющие две равные стороны, которые называются боковыми (AB и BC). Третья сторона – это основание (AC). В данной фигуре углы при основании равны (∠BAC = ∠BCA).

6. Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

Свойства треугольника

1. Любая из сторон треугольника меньше двух оставшихся, но больше их разности. Для удобства примем стандартные обозначения сторон – a, b и с. Тогда:

b – c < a < b + c, при b > с

Это свойство применяется для проверки отрезков на предмет того, могут ли они образовывать треугольник.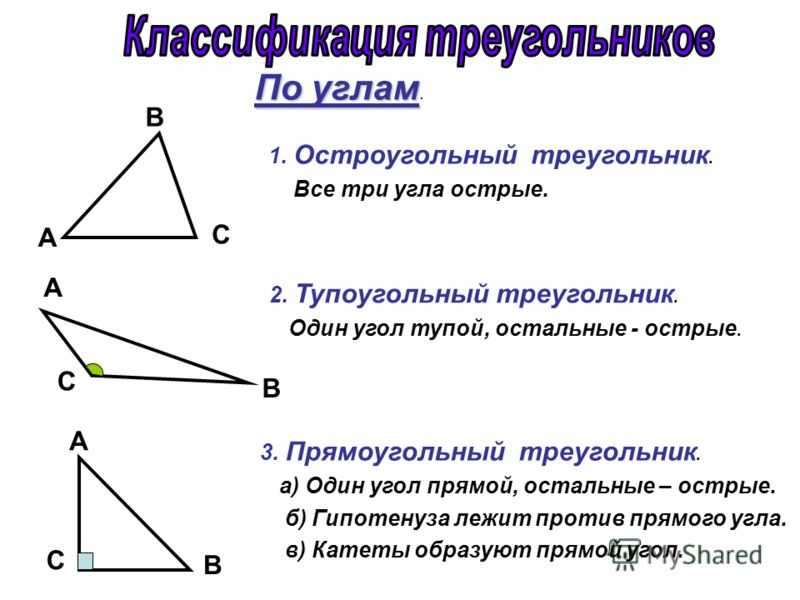

2. Сумма углов любого треугольника равняется 180°. Из этого свойства следует, что в тупоугольном треугольнике два угла всегда являются острыми.

3. В любом треугольнике напротив большей стороны находится больший угол, и наоборот.

Примеры задач

Задание 1В треугольнике известны два угла – 32° и 56°. Найдите значение третьего угла.

РешениеПримем известные углы за α (32°) и β (56°), а неизвестный – за γ.Согласно свойству о сумме всех углов, α + β + γ = 180°.Следовательно, γ = 180° – α – β = 180° – 32° – 56°  = 92°.

Задание 2Даны три отрезка длиной 4, 8 и 11. Выясните, могут ли они образовать треугольник.

РешениеСоставим неравенства для каждого из заданных отрезков, исходя из свойства, рассмотренного выше:11 – 4 < 8 < 11 + 48 – 4 < 11 < 8 + 411 – 8 < 4 < 11 + 8

Все они верны, следовательно, данные отрезки могут быть сторонами треугольника.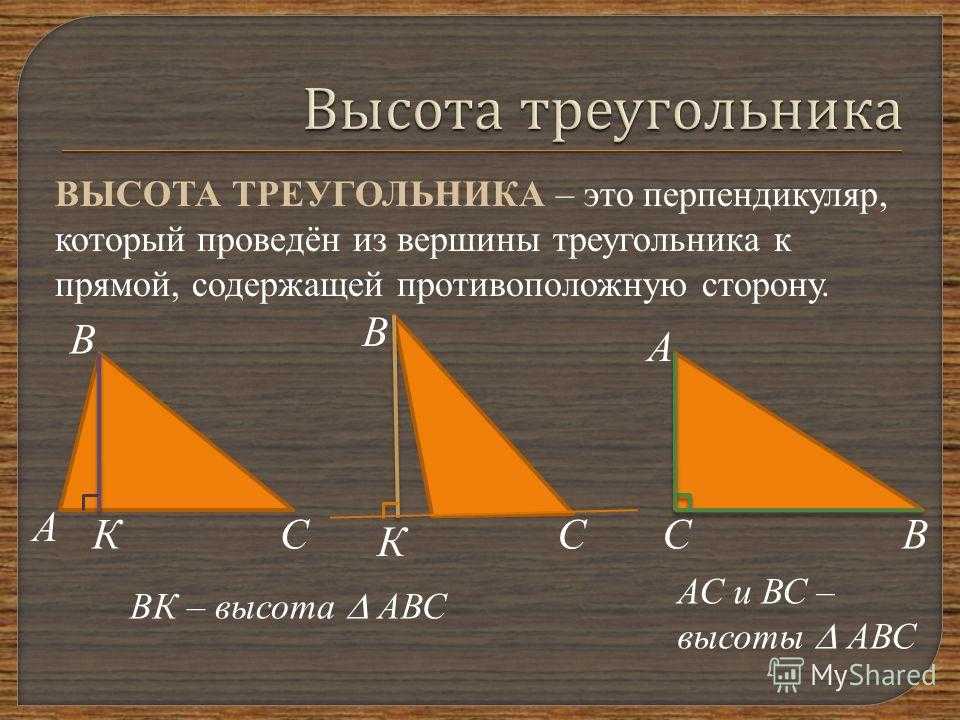

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов прямоугольного треугольника равна 90 градусов.

2. Катет прямоугольного треугольника, противолежащий углу в 30 градусов, равен половине гипотенузы. (Эта нога называется маленькой ногой.)

3. Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине и радиусу описанной окружности (R)

4. Медиана прямоугольного треугольника, проведенная к гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты этого треугольника.

$CD=AC=CB=R$

5. В прямоугольном треугольнике радиус вписанной окружности равен: $r={a+bc}/{2}$ , где $a$ и $b$ — катеты, $c$ — гипотенуза.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$AC^2+BC^2=AB^2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $ABC$ с прямым углом $C$

Для острого угла $B: AC$ — противолежащий катет; $ВС$ — соседняя ветвь.

Для острого угла $A: BC$ — противолежащий катет; $AC$ — соседняя нога.

1. Синус (sin) острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе.
2. Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенс (tg) острого угла прямоугольного треугольника – это отношение противолежащего катета к прилежащему катету.
4. Котангенс (ctg) острого угла прямоугольного треугольника — это отношение прилежащего катета к противолежащему.
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы различаются по знаку: для острых углов положительные значения, для тупых углов отрицательные значения

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$сина$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$тга$	${√3}/{3}$	$1$	$√3$
$ctga$	$√3$	$1$	${√3}/{3}$

Неравенство треугольника

Следующий факт касается не углов, а сторон треугольника.

Это означает, что:

• \( a+b>c\)
• \( a+c>b\)
• \( b+c>a\)

Ты уже догадался, почему этот факт называется неравенством треугольника?

Ну вот, а где же это неравенство треугольника может оказаться полезным?

А представь, что у тебя есть три друга: Коля, Петя и Сергей.

И вот, Коля говорит: «От моего дома до Петиного \( 100\) м по прямой». А Петя: «От моего дома до дома Сергея \( 200\) метров по прямой». А Сергей: «Вам хорошо, а от моего дома до Колиного аж \( 500\) м по прямой».

Ну, тут уже ты должен сказать: «Стоп, стоп! Кто – то из вас говорит неправду!»

Так не может быть!

Почему?

Да потому что если от Коли до Пети \( 100\) м, а от Пети до Сергея \( 200\) м, то от Коли до Сергея точно должно быть меньше \( 300\) (\( =100+200\)) метров – иначе и нарушается то самое неравенство треугольника.

Ну и здравый смысл точно, естественно, нарушается: ведь всякому с детства неизвестно, что путь до прямой (\( КС\)) должен быть короче, чем путь с заходом в точку \( П\). (\( К-П-С\)).

Так что неравенство треугольника просто отражает этот общеизвестный факт. Ну вот, ты теперь знаешь, как отвечать на такой, скажем, вопрос:

Бывает ли треугольник со сторонами \( 1,3,7\)?

Ты должен проверить, правда ли, что любые два числа из этих трёх в сумме больше третьего. Проверяем: \( 1+3<7\), значит, треугольника со сторонами \( 1,3\) и \( 7\) не бывает! А вот со сторонами \( 2,4,5\) – бывает, потому что

Виды треугольников по сторонам

Определение. Треугольник, у которого все три стороны разной длины называется разносторонним треугольником.

Определение. Треугольник, у которого две стороны равной длины, называется равнобедренным треугольником.

Определение. Треугольник с тремя равными сторонами называется равносторонним треугольником.

— А как еще различают треугольники? — задал новый вопрос Бим. — Вот у этих трех конфет все углы острые, а они все равно разные!

Бим взял конфеты и приложил по очереди одну конфету к другой:

— У каждой конфеты есть по одной одинаковой стороне. Но они разные. Как такое может быть?

— Значит другие стороны у них не будут одинаковыми, — нашлась Оля.

Оля достала еще один листочек и измерила у первой конфеты все три стороны:

— У первой конфеты все стороны разной длины. Выходит, конфета имеет вид треугольника с разными сторонами. Треугольник, у которого все стороны разной длины, называется разносторонним треугольником.

Тут у вас еще много конфет. — вмешался Коля. — Вот еще конфета с прямым углом и со сторонами разной длины.

А вот конфета с тупым углом, а стороны у нее все разные, — продолжил Вася.

Бим измерил стороны второй конфеты из трех, которые он взял.

— А у этой конфеты две стороны одинаковой длины, а у третьей стороны другая длина!

— Эта конфета имеет вид равнобедренного треугольника, — ответил Вася. — Треугольник, у которого две стороны имеют одинаковую длину, называется равнобедренным.

— И у прямоугольного треугольника могут быть две стороны одинаковые, и он тоже будет называться равнобедренным, — дополнила Оля.

— И у тупоугольного треугольника могут быть две стороны равными, и он тоже будет называться равнобедренным, — закончил перечисление Коля.

Бом измерил стороны третьей конфеты, которую взял Бим.

— А у этой конфеты все стороны одинаковой длины.

— Такой треугольник называется равносторонним, — объяснил Коля. — У него равны все стороны и все углы.

И тут зазвенел первый звонок.

— Ребята, пожалуйста, проходите в цирк, — пригласил Бом. — Уже скоро представление. Пойдем, Бим, и мы готовиться к выходу на арену.

— Сейчас бегу! — поспешно крикнул Бим. — Только для ребят запишу вопросы. И чтобы мне не опоздать, попросим ребят записать на них ответы.

Домашнее задание

1. Дайте определение равнобедренного треугольника.
2. В чем особенность этого треугольника?
3. Чем отличается равнобедренный треугольник от прямоугольного?
4. Назовите известные вам свойства равнобедренного треугольника.
5. Как вы думаете, можно ли на практике проверить равенство углов при основании и как это сделать?

Задание

А теперь давайте проведем небольшой блиц-опрос и узнаем, как вы усвоили новый материал.

Послушайте внимательно вопросы и ответьте верно ли такое утверждение, что:

1. Треугольник можно считать равнобедренным, если у него две стороны равны?
2. Биссектрисой называют отрезок, который соединяет вершину треугольника с серединой противоположной стороны?
3. Биссектрисой является отрезок, который делит угол, который соединяет вершину с точкой противоположной стороны пополам?

Советы относительно решения задач о равнобедренном треугольнике:

1. Для определения периметра равнобедренного треугольника достаточно умножить длину боковой стороны на 2 и сложить это произведение с длиной основы треугольника.
2. Если в задаче известны периметр и длина основы равнобедренного треугольника, то для нахождения длины боковой стороны достаточно отнять длину основы от периметра и найденную разницу разделить на 2.
3. А чтобы найти длину основы равнобедренного треугольника, зная и периметр, и длину боковой стороны, необходимо всего лишь умножить боковую сторону на два и отнять это произведение от периметра нашего треугольника.

Задачи:

1. Среди треугольников на рисунке определите один лишний и объясните свой выбор:

2. Определите, какие из изображенных на рисунке треугольников являются равнобедренными, назовите их основы и боковые стороны, а так же рассчитайте их периметр.

3. Периметр равнобедренного треугольника равен 21 см. Найдите стороны этого треугольника, если одна из них больше на 3 см. Какое количество решений может иметь данная задача?

4. Известно, что если боковая сторона и противолежащий основе угол одного равнобедренного треугольника равен боковой стороне и углу другого, то эти треугольники будут равны. Докажите это утверждение.

5. Подумайте и скажите, является ли любой равнобедренный треугольник равносторонним? И будет ли любой равносторонний треугольник равнобедренным?

6. Если стороны равнобедренного треугольника равны 4 м и 5 м, то каков будет его периметр? Сколько решений может иметь эта задача?

7. Если один из углов равнобедренного треугольника равен 91 градусу, то чему равны остальные углы?

8. Подумайте и ответьте, какие углы должны быть у треугольника, чтобы он одновременно был и прямоугольным, и равнобедренным?

Другие свойства равнобедренного треугольника

Положение центра окружности, описанной вокруг равнобедренного треугольника, зависит от величины угла вершины. Так, если равнобедренный треугольник остроугольный, центр круга располагается внутри фигуры.

Центр окружности, которая описана вокруг тупоугольного равнобедренного треугольника, лежит вне его. И, наконец, если величина угла при вершине равна 90°, центр лежит ровно на середине основания, а через само основание проходит диаметр окружности.

Для того чтобы определить радиус окружности, описанной около равнобедренного треугольника, достаточно разделить длину боковой стороны на удвоенный косинус половины величины угла при вершине.

Материал 7 класса

В равнобедренном треугольнике углы при основании равны, а биссектриса, проведенная к основанию, является медианой и высотой.

Если в треугольнике два угла равны, то он равнобедренный.

Из любой точки окружности ее диаметр, не выходящий из этой точки, виден под прямым углом.

Внешний угол треугольника

Внешний угол треугольника — угол, образованный стороной треугольника и продолжением его другой стороны.

При каждой вершине треугольника имеются два внешних угла.

Внешний угол треугольника равен сумме двух углов, не смежных с ним.

Откуда в математике могли появиться внешние углы. Когда европейцы увидели пирамиды древнего Египта, они были потрясены увиденным. Им захотелось измерить эти грандиозные сооружения. Вот только внутренний угол пирамиды измерить не представляется возможным. Можно измерить внешний угол и высчитать внутренний.

Внутренняя область треугольника ABC — общая часть внутренних областей трех углов А, В и С этого треугольника.

Признаки равенства треугольников

1. СУС — Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. УСУ — Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
3. ССС — по трем сторонам (= это означает, что треугольник жесткая фигура — стороны определяют углы)

Дополнительные признаки

• СМС — Два треугольника равны, если две стороны и медиана, проведенная из общей вершины этих сторон, одного треугольника соответственно равны двум сторонам и медиане, проведенной из общей вершины этих сторон, другого треугольника.
• По медиане и двум углам, на которые она делит угол треугольника
• МСМ — Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника, то такие треугольники равны.
• СБС — Ели две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника, то такие треугольники равны.
• МММ — Два треугольника равны, если три медианы одного треугольника соответственно равны трем медианам другого треугольника.
• ВВВ — Два треугольника равны, если три высоты одного треугольника соответственно равны трем высотам другого треугольника.
• БББ — По трем биссектрисам
• ССУ_б — Если две стороны одного треугольника соответственно равны двум сторонам другого, и угол одного треугольника, лежащий против большей из сторон, равен соответствующему углу другого, то такие треугольники равны.

Треугольник — жесткая фигура

Жесткая фигура — это фигура, не подверженная деформации.

Соединив дощечки с помощью гвоздей в четырехугольник, можно изменять градусную меру углов    четырехугольника, не меняя длины его сторон.

Можно менять величины углов у пятиугольников, шестиугольников и многоугольников с большим количеством сторон.

С треугольником так поступить не удастся.  Стороны треугольника определяют его углы однозначно. Треугольник не подвержен деформации. Поэтому треугольник — жесткая фигура. Из всех многоугольников только треугольник является жесткой фигурой.

Это свойство треугольника используется, в частности, при создании железных ажурных конструкций. Мосты, башни, подъемные краны, каркасы зданий, опоры для высоковольтных линий электропередач изготавливают таким образом, чтобы они содержали как можно больше треугольных элементов.

Средняя линия треугольника

Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника.

При проведении всех трёх средних линий образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2. Центральный из этих 4 одинаковых треугольников называется дополнительным треугольником. Медианы и центр тяжести данного треугольника ABC совпадают с медианами и центром тяжести дополнительного треугольника A’B’C’.

Средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четверти площади исходного треугольника.

См. также

• Треугольник и окружность

• Неравенство треугольника

Теорема о сумме углов треугольника

Если один угол треугольника становится больше, остальные углы «сжимаются». Выражаясь метафорично, треугольник — это фигура жесткой сцепки.

Отсюда и создается впечатление, что сумма углов треугольника будто бы всегда одна и та же, вне зависимости от того, сколько какому углу построением отмерено градусов.

А еще внимательный читатель мог заметить, что равенство накрест лежащих углов при параллельных и сумма односторонних углов в $180^\circ$, если крепко призадуматься, подает сигнал в том числе: сумма углов треугольника, скорее всего, также равняется $180^\circ$.

Нам остается проверить данные наблюдения и доказать их:

Доказательство

Начертим произвольный треугольник $\bigtriangleup{ABC}$. Расположим его на чертеже боковой стороной $AB$, а на основании $BC$ отметим середину — точку $O$. Продолжим медиану $AO$ от основания и отложим равный медиане отрезок $OA_1$.

Рассмотрим треугольники $\bigtriangleup{ABO}$ и $\bigtriangleup{OA_{1}C}$. Треугольники равны по первому признаку: $AO=OA_1$, $BO=OC$, углы $\angle{BOA}$ и $\angle{A_{1}OC}$ равны как вертикальные. Из равенства треугольников следует, что $\angle{ABC}=\angle{A_{1}CB}$.

Заметим, что $\angle{ABC}$ и $\angle{A_{1}CB}$ — накрест лежащие углы при отрезках $AB$ и $CA_1$ и секущей $CB$. Следовательно $AB\parallel{CA_1}$.

Рассмотреть эти же отрезки можно при секущей $CA$. Раз отрезки параллельны, то сумма односторонних углов $\angle{A}$ и $\angle{A_{1}CA}$ равна $180^\circ$. Поскольку накрест лежащие $\angle{ABC}$ и $\angle{A_{1}CB}$ равны, а $\angle{A_{1}CA}=\angle{ACB}+\angle{ABC}$, то выходит:

$$\angle{A}+\angle{A_{1}CA}=180^\circ\\\angle{A}+\angle{ABC}+\angle{ACB}=180^\circ$$

Это и есть сумма углов треугольника $\bigtriangleup{ABC}$. Теорема доказана.

{"questions":}

Сумма углов треугольника: комментарий к доказательству

Совершенно нормальный вопрос при изучении геометрии: «Почему именно такой нестандартный чертеж?! Боковой стороной?»

Располагать треугольник на чертеже боковой стороной — нетипичная практика. Обычно мы рисуем эту фигуру по принципу его геометрического значка — $\bigtriangleup$. Однако допустите мысль, что теоремы об углах при параллельных таки навели вас на мысли, чему может равняться сумма углов треугольника. Что бы вы сделали первым делом при чертеже к доказательству?

Расположили бы треугольник таким образом, чтобы его стороны «играли роль» потенциальных секущих, а третья сторона —  «роль» одной из возможных параллельных прямых.

Так что подобный чертеж — попытка сразу «подогнать» ситуацию к удобному графическому использованию уже ранее доказанных теорем. Это — геометрическая сноровка. Так что не переживайте, если иногда кажется, что IQ рисовавшего чертеж уж слишком переваливает за 300… Сноровка вырабатывается со временем. Практикуйтесь и вы сможете так же!

Следствие из теоремы о сумме углов треугольника

Напомним, что острым считается угол меньше $90^\circ$. Исходя из того, что сумма углов треугольника — всегда $180^\circ$, логично заключить невозможность наличия в треугольнике двух тупых углов. Сумма двух тупых углов всегда больше $180^\circ$. А это противоречит теореме о сумме углов треугольника.

{"questions":[{"content":"`image-12` Если помните, следствия, как и теоремы, все-таки требуют доказательства. Вдруг мы вынесли ложное умозаключение? Следствие мы, да, только что доказали, но очень нестрого, практически «на пальцах». Ниже приведено строгое доказательство следствия из теоремы о сумме углов треугольника. Ваша задача в качестве практики — восстановить порядок положений доказательства.   `sorter-1`","widgets":{"sorter-1":{"type":"sorter","items":},"image-12":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/04/oh-1.svg","width":"300"}}}]}