Теорема чевы и менелая — формулировка, применение и примеры решения

Формулировка теоремы Чевы

Джованни Чева — итальянский математик, инженер. Годы жизни 1648 — 1734 гг. Основные труды ученого в области геометрии и механики.

Рассматриваемая теорема была доказана ученым в 1678 г. 

Рассмотрим приведённый ниже рисунок:

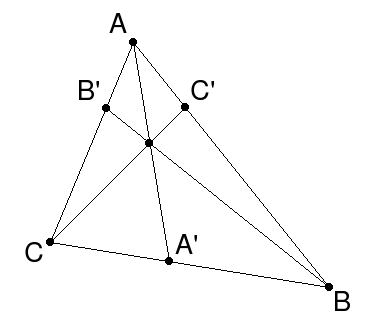
Теорема звучит так: любые произвольные отрезки, выходящие из вершин треугольника, (но с одним условием: они должны пересекаться в одной точке) делят противолежащие этим вершинам стороны таким образом, что истинно равенство:

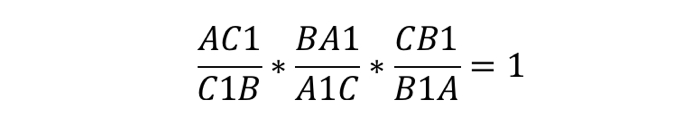
В честь ученого, доказавшего эту теорему, данные отрезки называют «чевианами». 

Доказательство теоремы

Рассмотрим рисунок:

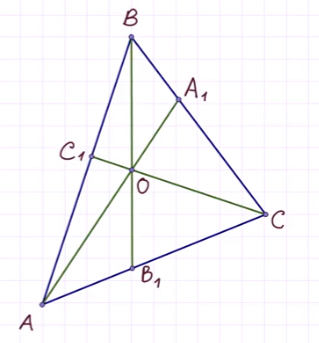
Итак, мы имеем треугольник ABC и произвольные чевианы AA1 и BB1.

Третья чевиана CC1 обязательно должна проходить через точку пересечения первых двух. При этом получается, что:

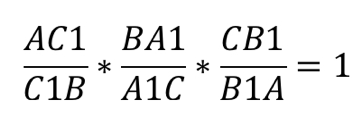
Обозначим за O точку пересечения данных прямых.

Продлим медиану BB1.

Проведём перпендикуляры из вершин A и С таким образом:

Запишем соотношение:

Треугольники AKB₁ и CNB₁
подобны по острому углу. 

Аналогично получаем:

Теперь перемножим равенства:

что и требовалось доказать.

Примеры решения задач

Задача 1

Треугольник АВС обладает сторонами АВ и ВС, на которых отмечены точки D и Е соответственно. Также справедливо равенство:

\(AD=\frac{3}{8}AB\)

\(BE=\frac{1}{5}BC\)

Отрезки АЕ и CD пересекают друг друга в точке F, как показано на рисунке. Требуется определить отношение отрезков АЕ и CD, поделенных точкой F.

Решение

Следует использовать теорему Менелая для треугольника BCD.

В таком случае:

\(\frac{BE}{EC}\times \frac{CF}{FD}\times \frac{DA}{AB}=1\Rightarrow \frac{1}{4}\times \frac{CF}{FD}\times \frac{3}{8}=1\Rightarrow \frac{CF}{FD}=\frac{32}{3}\)

Необходимо применить теорему Менелая для треугольника АВЕ.

\(\frac{AD}{DB}\times \frac{BC}{CE}\times \frac{EF}{FA}=1\Rightarrow \frac{3}{5}\times \frac{5}{4}\times \frac{EF}{FA}=1\Rightarrow \frac{EF}{FA}=\frac{4}{3}\)

Ответ: \( \frac{CF}{FD}=\frac{32}{3}\), \( \frac{EF}{FA}=\frac{4}{3}\)

Задача 2

На рисунке изображен треугольник. Исходя из его характеристик, необходимо определить отношение \(\frac{x}{y}\)

Согласно теореме Менелая, получим равенство:

\(\frac{x}{y}\times \frac{5}{1}\times \frac{2}{3}=1\)

Таким образом:

\( \frac{x}{y}=\frac{3}{10}\)

Ответ: \( \frac{3}{10}\)

Задача 3

На рисунке изображена геометрическая фигура в виде треугольника. Исходя из данных на схеме, требуется рассчитать отношение \(\frac{x}{y}\)

Решение

Руководствуясь теоремой Менелая, запишем уравнение:

\(\frac{x}{y}\times \frac{1}{2}\times \frac{4a}{3a}=1\)

Таким образом:

\(\frac{x}{y}=\frac{3}{2}\)

Применение теорем Чевы и Менелая при решении задач ЕГЭ

Теорема Менелая (как и обратная) применима и в первой части экзаменационного бланка, и в 16-м задании. Рассмотрим пару таких задач.

Задача 1

Дан треугольник ABC (см. рисунок ниже) с продолжением стороны CA. Также проведены медианы BM и AN. Точку их пересечения обозначим за O.

Возьмём точку K на стороне AB, такую, что AK относится к AB, как 1/3.

Проведём прямую OK до пересечения со стороной AC. Точку их пересечения обозначим за P.

Сторону AP обозначим за y.

Найти: чему равен отрезок AP.

Так как отношение сторон AB и AK равно 1/3, следовательно, AK = x, а KB = 3x.

Рассмотрим треугольник ABM. Для него берём прямую OP.

Таким образом мы нашли искомые точки P, A, M, O, K и B.

Запишем теорему Менелая к данному рисунку.

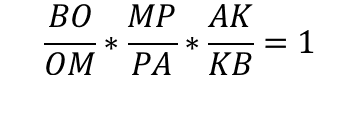
Подставляем в это соотношение известные данные:

В итоге мы получаем, что y = 4.

Ответ: отрезок AP = 4 см.

Задача 2

Задача, связанная со свойствами теоремы Чевы.

сумма AB и BC равна 13;

Найти: отношение BO и OB1.

Итак, запишем отношение:

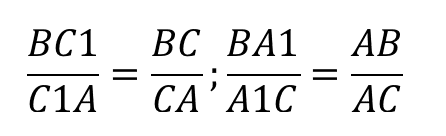
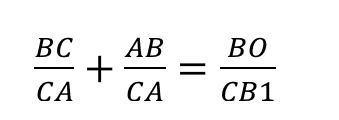
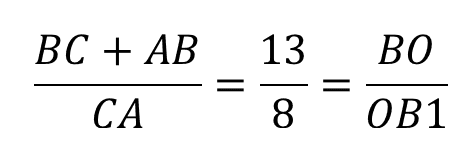
Конечным результатом является дробь 13/8.

https://youtube.com/watch?v=6-icW_4gatM

Слайды и текст этой презентации

Слайд 1Теорема Менелая и ее применение при решении задач
(подготовка к

Слайд 2СодержаниеТеоретические факты: а) пропорциональные отрезки в треугольниках б)

Слайд 3Теоретические фактыТеорема Фалеса Параллельные прямые пересекая стороны

1. Если угол одного треугольника равен углу другого треугольника, то отношение площадей этих треугольников равно отношению произведений сторон, содержащих эти углы

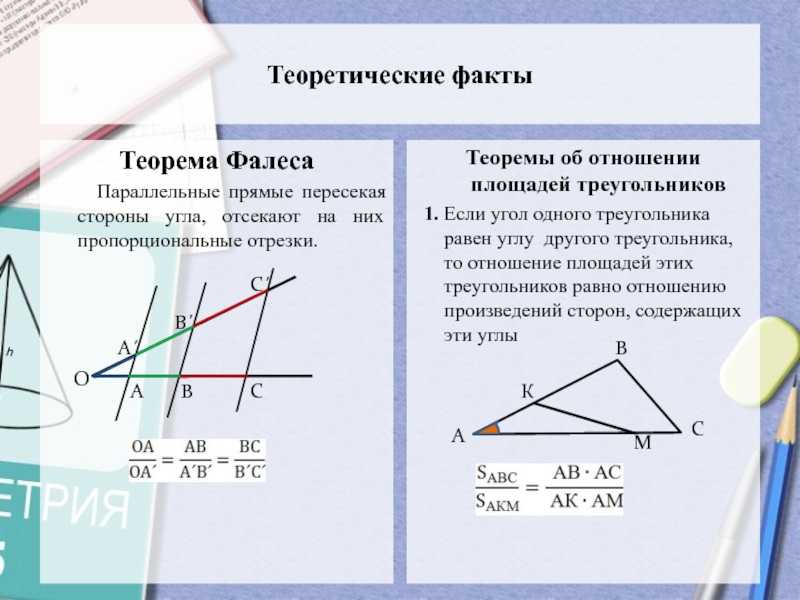
Слайд 4Теоремы об отношении площадей треугольников2. Пусть ∆АВС и ∆АВD имеют

общую сторону АВ. Тогда отношение их площадей равно отношению высот,

проведенных из вершин С и D. S(∆АВС) : S(АВD) = СР:DQ.

3.Отношение площадей треугольников, имеющих равные высоты равно отношению оснований: S(∆АВС) : S(АВD) =AC:АD.

А

В

С

D

P

Q

А

В

С

D

P

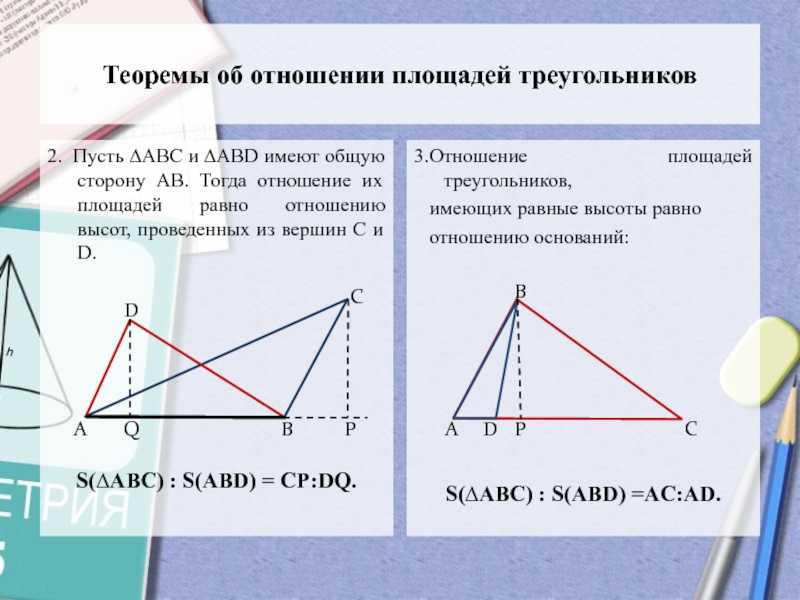
АВС и на продолжении стороны АВ за вершину В расположены

точки М и К соответственно, причем ВМ:МС = 4:5 и ВК:АВ=1:5. Прямая КМ пересекает сторону АС в точке N. Найти отношение СN: АN.

Решение Проведем ВР параллельно КМ.По теореме Фалеса для угла NАК:По теореме Фалеса для угла ВСР:4. Итак, z=4d, тогда АN=6z=24d, значит СN:АN=5:24.Ответ: 5:24

А

С

В

М

К

N

4х

5х

у

5у

Р

5z

z

N

4x

5d

4d

Слайд 6 Предложенный вариант решения задачи – один из традиционных,

без применения теоремы Менелая. Рассмотрим другой (более рациональный) способ

решения, применяя указанную теоремуТеорема Менелая Пусть на сторонах AB, BC и на продолжении стороны AC ∆ABC взяты соответственно точки С´, А´ и В´, не совпадающие с вершинами ∆ABC. Точки лежат на одной прямой тогда и только тогда, когда выполняется равенство Для дальнейшего решения задач воспользуемся необходимым условием данной теоремы.

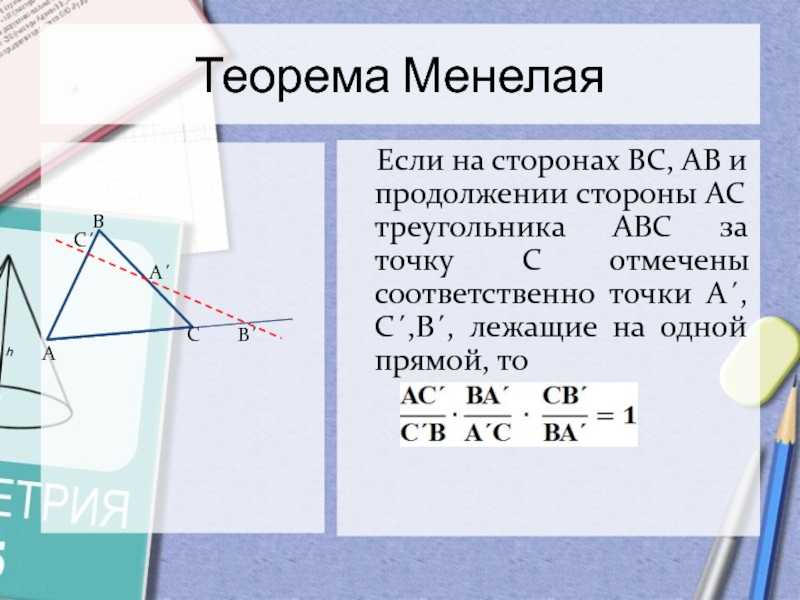
Слайд 7Теорема Менелая Если на сторонах ВС, АВ и продолжении

стороны АС треугольника АВС за точку С отмечены соответственно точки

А´, С´,В´, лежащие на одной прямой, то

В

А

С

В´

А´

С´

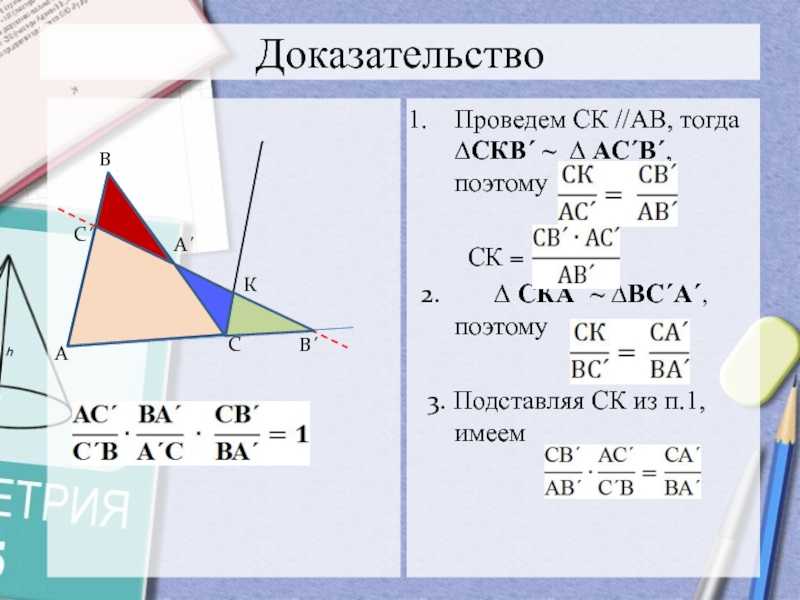
Слайд 8ДоказательствоПроведем СК //АВ, тогда ∆СКВ´ ~ ∆ АС´В´, поэтому

СК = 2.

∆ СКА´ ~ ∆ВС´А´, поэтому 3. Подставляя СК из п.1, имеем

В

А

С

В´

К

А´

С´

стороне ВС треугольника АВС и на продолжении стороны АВ за

вершину В расположены точки М и К соответственно, причем ВМ:МС = 4:5 и ВК:АВ=1:5. Прямая КМ пересекает сторону АС в точке N. Найти отношение СN: АN.

Стрелки на рисунке (от точки А) показывают, как легко запомнить последовательность отрезков в пропорции. Найдем Ответ:

А

С

В

N

M

K

4х

5х

у

5у

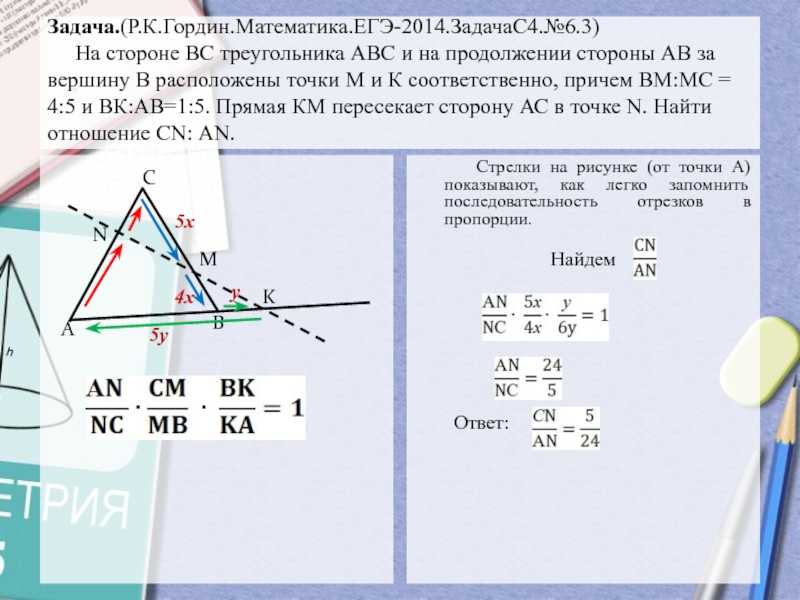
треугольнике АВС АВ=с, ВС=а, АС=в. В каком отношении центр вписанной

окружности треугольника делит биссектрису СD?

Решение:Для треугольника ВСD и секущей АК: Найдем ДА: = ДА = 3. Найдем :

В

С

А

К

D

О

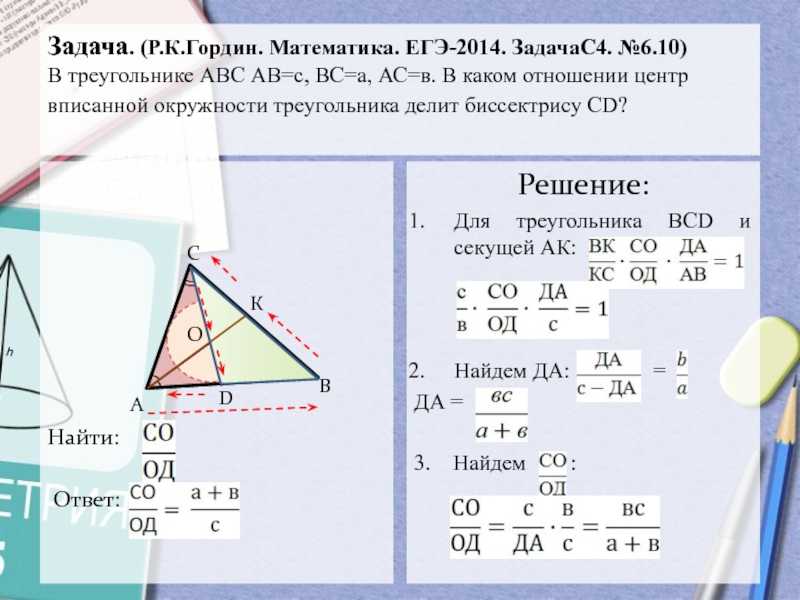
№6.14)
В ∆АВС, площадь которого равна 6, на стороне

АВ взята т.К, делящая эту сторону в отношении АК:ВК=2:3, а на стороне АС взята т. L, делящая АС в отношенииAL:LС=5:3. Точка Q пересечения прямых СК и ВL отстоит от прямой АВ на расстояние 1,5. Найти сторону АВ.

Решение: Для тр. АСК и секущей ВL найдем отношение CQ:QK. 2. Проведем высоту СР. СР// QH. 3. По теореме Фалеса Н – середина РК, тогда QH-средняя линия СРК, значит СР=3.4. S (АВС) =0,5 АВ•СР, тогда АВ=2S(АВС) :СР=4.Ответ: АВ = 4.

L

Q

H

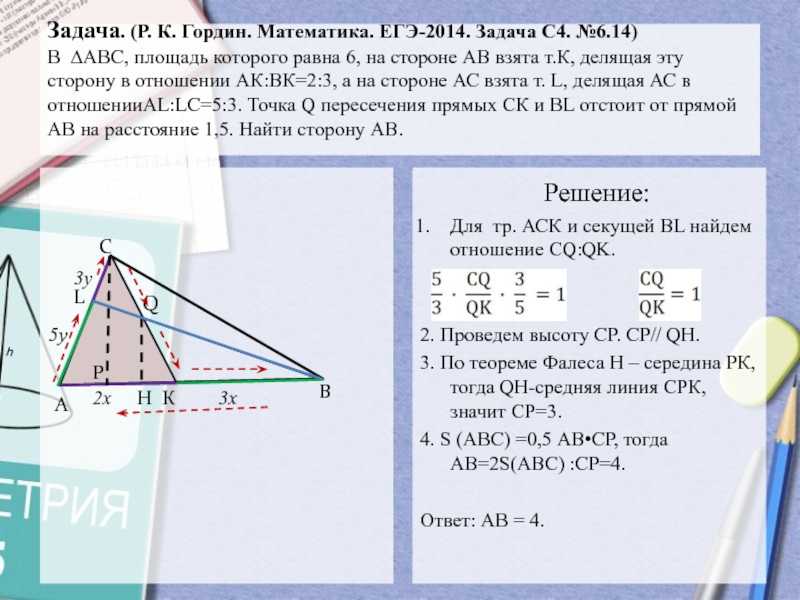
А.Л.Семенова, И.В.Ященко. Трениров.работа 28. С4)
На сторонах АВ, ВС и

АС ∆АВС взяты соответственно точки К, L и М, причем
АК:КВ=2:3, ВL:LС=1:2, СМ:МА=3:1. В каком отношении отрезок КL делит отрезок ВМ?

Найти Ответ:

Решение:Для ∆АВС и секущей КL: 2. АР = РС = АС = 4z =2z, значит =3. Для ∆АВМ и секущей КL:

М

К

L

2х

3х

у

2у

3z

z

О

Р

2z

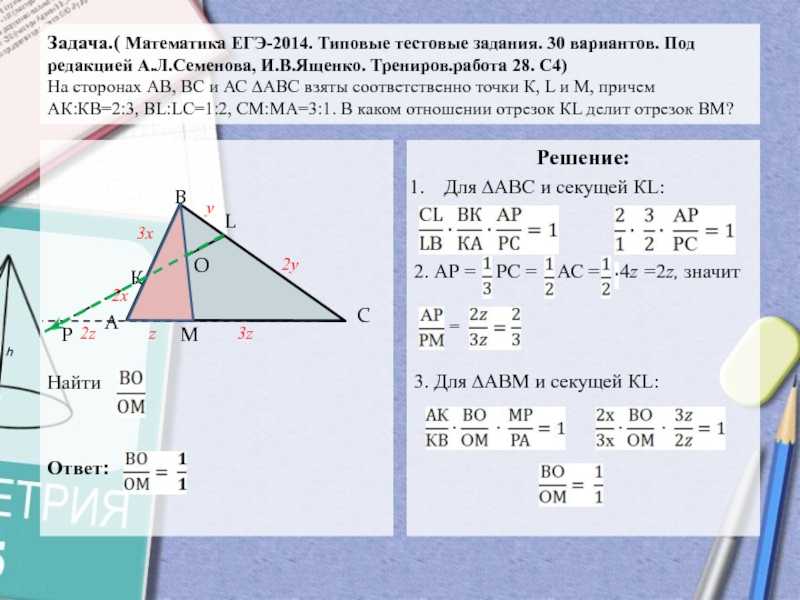
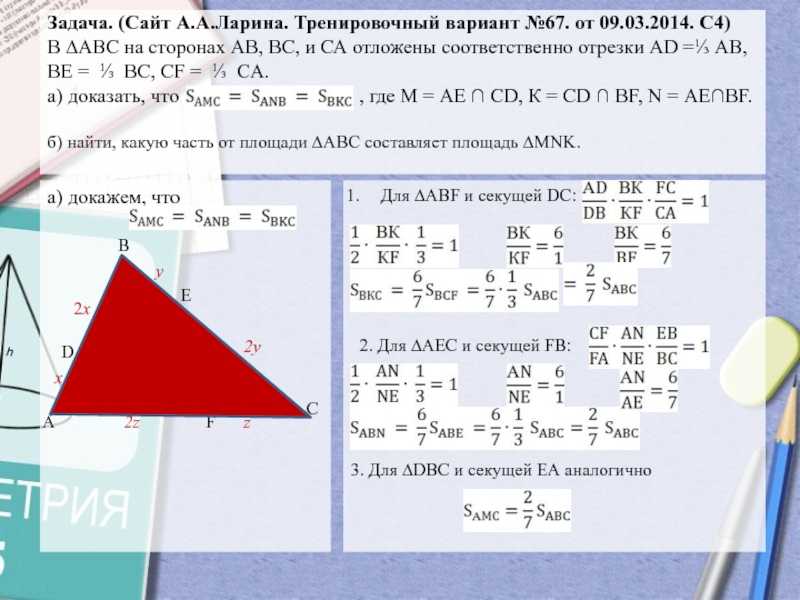
Слайд 13Задача. (Сайт А.А.Ларина. Тренировочный вариант №67. от 09.03.2014. С4)
В

∆АВС на сторонах АВ, ВС, и СА отложены соответственно отрезки

АD =⅓ АВ,
ВЕ = ⅓ ВС, СF = ⅓ CА.
а) доказать, что , где М = АЕ ∩ СD, К = СD ∩ ВF, N = АЕ∩ВF.

б) найти, какую часть от площади ∆АВС составляет площадь ∆MNK.

а) докажем, что

Для ∆АВF и секущей DC: 2. Для ∆АЕС и секущей FВ: 3. Для ∆DBC и секущей ЕА аналогично

х

2х

у

2у

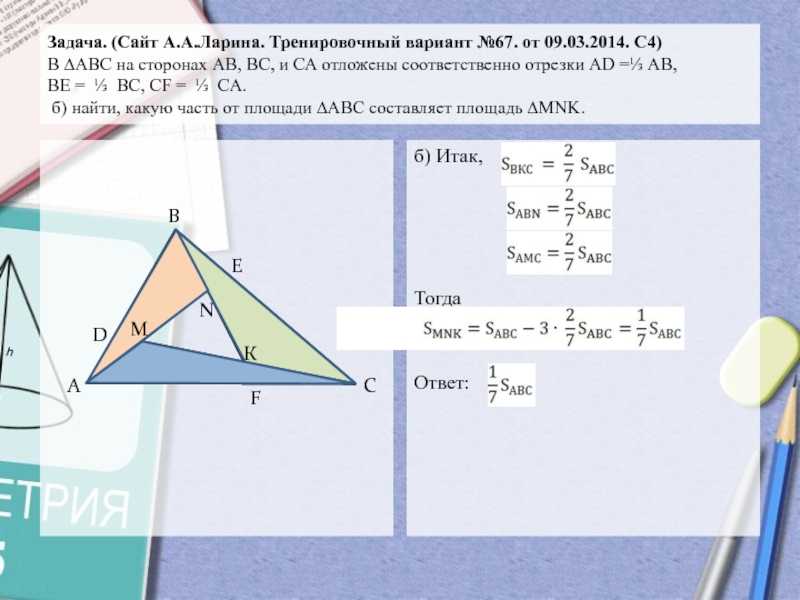
Слайд 14Задача. (Сайт А.А.Ларина. Тренировочный вариант №67. от 09.03.2014. С4)
В

∆АВС на сторонах АВ, ВС, и СА отложены соответственно отрезки

АD =⅓ АВ,
ВЕ = ⅓ ВС, СF = ⅓ CА.
б) найти, какую часть от площади ∆АВС составляет площадь ∆MNK.

б) Итак,ТогдаОтвет:

А

В

С

D

E

F

М

N

K

М

К

Слайд 15Заключение
Решение задач с помощью теоремы Менелая более рационально,

чем их решение другими способами, требующими дополнительных действий и построений,

которые не всегда оказываются очевидными. Теорема Менелая помогает быстро и оригинально решить задачи повышенной сложности, в том числе и задачи уровня С единого государственного экзамена.

Используемая литератураЕГЭ 2014.Математика. Задача С4. Гордин Р.К. Под ред. Семенова А.Л.2013г.Математика. ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под ред. А.Л.Семенова, И.В.Ященко. 2014г.http://alexlarin.net/ege/2014/trvar67.html

Замечание

Из определения следуют свойства:

1. Можно менять знак: $\dfrac{\overrightarrow{AB}}{\overrightarrow{CD}}=-\dfrac{\overrightarrow{AB}}{\overrightarrow{DC}}$
2. Можно «сокращать»: $\dfrac{\overrightarrow{AB}}{\overrightarrow{CD}}\cdot \dfrac{\overrightarrow{CD}}{\overrightarrow{EF}}=\dfrac{\overrightarrow{AB}}{\overrightarrow{EF}}$
3. Можно делить обе части равенства на отношение: если $\dfrac{\overrightarrow{AB}}{\overrightarrow{CD}}=\dfrac{\overrightarrow{EF}}{\overrightarrow{KL}}$, то $\dfrac{\overrightarrow{AB}}{\overrightarrow{CD}}\cdot\dfrac{\overrightarrow{KL}}{\overrightarrow{EF}}=1$

Теорема Менелая

Точки $A_1,B_1$ и $C_1$, лежащие на сторонах треугольника $ABC$ или
на их продолжениях, лежат на одной прямой тогда и только тогда,
когда
$\dfrac{\overrightarrow{AC_1}}{\overrightarrow{C_1B}}\cdot\dfrac{\overrightarrow{BA_1}}{\overrightarrow{A_1C}}\cdot\dfrac{\overrightarrow{CB_1}}{\overrightarrow{B_1A}}=-1$.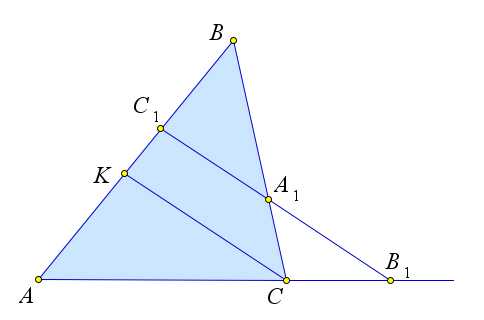

Доказательство

Докажем прямую теорему

Рассмотрим треугольник $ABC$, и пусть прямая $l$ пересекает стороны
$AB, BC, CA$ или их продолжения в точках $C_1, A_1$ и $B_1$
соответственно.

Докажем, что тогда
$\dfrac{\overrightarrow{AC_1}}{\overrightarrow{C_1B}}\cdot\dfrac{\overrightarrow{BA_1}}{\overrightarrow{A_1C}}\cdot\dfrac{\overrightarrow{CB_1}}{\overrightarrow{B_1A}}=-1$.

Проведем через вершину $C$ прямую $p$, параллельную прямой $l$.

Пусть $K$ – это точка пересечения прямых $p$ и $AC$.

По теореме Фалеса
$\dfrac{\overrightarrow{AB_1}}{\overrightarrow{B_1C}}=\dfrac{\overrightarrow{AC_1}}{\overrightarrow{C_1K}},
\dfrac{\overrightarrow{CA_1}}{\overrightarrow{A_1B}}=-\dfrac{\overrightarrow{C_1K}}{\overrightarrow{C_1B}}$.

Перемножив эти равенства, получим $\dfrac{\overrightarrow{AB_1}\cdot
\overrightarrow{CA_1}}{\overrightarrow{B_1C}\cdot
\overrightarrow{A_1B}}=-\dfrac{\overrightarrow{AC_1}}{\overrightarrow{C_1B}}$,
откуда следует, что
$\dfrac{\overrightarrow{AC_1}}{\overrightarrow{C_1B}}\cdot\dfrac{\overrightarrow{BA_1}}{\overrightarrow{A_1C}}\cdot\dfrac{\overrightarrow{CB_1}}{\overrightarrow{B_1A}}=-1$.

Докажем обратную теорему.

Рассмотрим треугольник $ABC$. Пусть на
прямых $AB, BC$ и $AC$ выбраны точки $C_1, A_1$ и $B_1$
соответственно.

Докажем, что если
$\dfrac{\overrightarrow{AC_1}}{\overrightarrow{C_1B}}\cdot\dfrac{\overrightarrow{BA_1}}{\overrightarrow{A_1C}}\cdot\dfrac{\overrightarrow{CB_1}}{\overrightarrow{B_1A}}=-1$,
то точки $A_1, B_1$ и $C_1$ лежат на одной прямой.

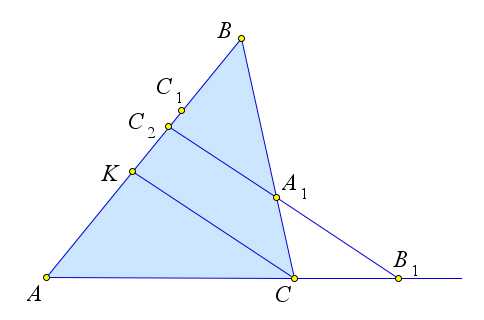
Пусть прямая $A_1B_1$ пересекает прямую $AB$ в точке $C_2$.

Докажем, что $C_2=C_1$.

Действительно, так как точки $A_1,
B_1$ и $C_2$ лежат на одной прямой, то для них выполняется равенство
$\dfrac{\overrightarrow{AC_2}}{\overrightarrow{C_2B}}\cdot\dfrac{\overrightarrow{BA_1}}{\overrightarrow{A_1C}}\cdot\dfrac{\overrightarrow{CB_1}}{\overrightarrow{B_1A}}=-1$.

Но тогда
$\dfrac{\overrightarrow{AC_2}}{\overrightarrow{C_2B}}=-\dfrac{\overrightarrow{A_1C}}{\overrightarrow{BA_1}}\cdot\dfrac{\overrightarrow{B_1A}}{\overrightarrow{CB_1}}=\dfrac{\overrightarrow{AC_1}}{\overrightarrow{C_1B}}$,
что и означает, что $C_1=C_2$.

Картинка может отличаться от той, что дана при доказательстве теоремы. Но все рассуждения останутся верны. (Нужен рисунок)