Вычитание двузначных, трехзначных и многозначных чисел столбиком

Принцип деления

Прежде чем приступать к объяснению алгоритма деления следует сформировать у ребенка понимание самого процесса.

Объясните маленькому ученику, что «деление» – это разделение единого целого на равные части.

Возьмите коробку карандашей, которая будет выступать единым целым (можно взять любые предметы – кубики, спички, яблоки и т. д.), и предложите ребенку разделить их поровну между собой и вами. Затем, попросите его сосчитать сколько карандашей было изначально в коробке и сколько он раздал каждому.

По мере понимания ребенка, увеличивайте число предметов и количество участников. Далее, следует отметить, что не всегда получается разделить поровну и некоторые предметы остаются «ничейными». Например, предложите разделить 9 груш между бабушкой, дедушкой, папой и мамой. Ребенок должен усвоить, что все получат по 2 груши, а одна окажется в остатке.

Как вычитать столбиком

Вычитание многозначных чисел обычно выполняют столбиком, записывая числа друг под другом (уменьшаемое сверху, вычитаемое снизу) так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Слева между числами ставится знак действия. Под вычитаемым проводят черту. Вычисление начинают с разряда единиц: из единиц вычитают единицы, затем из десятков — десятки и т. д. Результат вычитания записывают под чертой:

Рассмотрим пример, когда в каком-либо разряде цифра уменьшаемого меньше цифры вычитаемого:

От 2 мы не можем отнять 9, что нам делать в этом случае? В разряде единиц у нас нехватка, но в разряде десятков у уменьшаемого аж 7 десятков, поэтому мы можем один из этих десятков перекинуть в разряд единиц:

В разряде единиц у нас было 2, мы перекинули десяток, стало 12 единиц. Теперь мы легко можем от 12 отнять 9. Записываем под чертой в разряде единиц 3. В разряде десятков у нас было 7 единиц, одну из них мы перекинули в простые единицы, осталось 6 десятков. Записываем под чертой в разряде десятков 6. В результате мы получили число 63:

Вычитание столбиком обычно не записывают так подробно, вместо этого, над цифрой разряда, у которого будет занята единица, ставят точку, чтобы не запоминать, у какого разряда надо будет дополнительно вычесть единицу:

При этом говорят так: из 2 вычесть 9 нельзя, занимаем единицу, из 12 вычитаем 9 — получим 3, пишем 3, в разряде десятков у нас было 7 единиц, мы одну перекинули, осталось 6, пишем 6 .

Теперь рассмотрим вычитание столбиком из чисел, содержащих нули:

Начинаем вычитать. От 7 отнимаем 3, пишем 4. От нуля мы не можем отнять 5, поэтому мы вынуждены занять единицу в старшем разряде, но в старшем разряде у нас тоже 0, поэтому и для этого разряда мы вынуждены занять в более старшем разряде. Занимаем единицу из разряда тысяч, получаем 10 сотен:

Одну из единиц разряда сотен мы занимаем в младший разряд, получаем 10 десятков. Из 10 вычитаем 5, пишем 5:

В разряде сотен у нас осталось 9 единиц поэтому, от 9 отнимаем 6, пишем 3. В разряде тысяч у нас была единица, но мы её потратили на младшие разряды, поэтому здесь остаётся нуль (его записывать не надо). В результате мы получили число 354:

Такая подробная запись решения была приведена, чтобы было проще понять, как выполняется вычитание столбиком из чисел содержащих нули. Как уже упоминалось, на практике решение обычно записывается так:

А все упомянутые действия выполняются в уме. Чтобы было легче выполнять вычитание, запомните простое правило:

Если при вычитании столбиком над нулём стоит точка, нуль превращается в 9.

Взаимосвязь с таблицей умножения

Покажите ребенку, что «деление» противоположное действие «умножению».

• Возьмите таблицу умножения и покажите ученику взаимосвязь между двумя операциями.
• Например, 4х5=20. Напомните ребенку, что число 20 результат произведения двух чисел 4 и 5.
• Затем, наглядно покажите, что деление противоположный процесс: 20/5=4, 20/4=5.

Обратите внимание ребенка на то, что правильным ответом всегда будет множитель, не участвующий в делении. Разберите другие примеры

Разберите другие примеры.

Если ваш ребенок отлично будет знать таблицу умножения, и поймет взаимосвязь между двумя математическими операциями, он легко освоит деление. Стоит ли запоминать ее в обратном порядке – выбор за вами.

Методика деления в столбик

Существует определенный алгоритм для деления в столбик. Изучается он в начальных классах средних образовательных школ. Методику можно применять не только для положительных, но и отрицательных значений. При этом нужно учитывать знак:

1. Деление отрицательной величины на отрицательную — положительное значение.
2. При делении положительного на отрицательное или наоборот — отрицательная величина.

Алгоритм без остатка

Методика применяется в том случае, когда делимое является не простым числом, а содержит множители. Кроме того, при его делении на делитель, не соответствующий одному из признаков деления. Например, 33 делится на 2 с остатком. Однако, когда делитель равен 3, то последнего нет.

Для применения алгоритма нужно наглядно разобрать следующий пример: требуется разделить 78 на 2. Методика выполнения этой операции имеет следующий вид:

1. Записать делимое с левой стороны, а делитель — справа.
2. По карточке простых чисел или при помощи ручного метода необходимо определить принадлежность делимого к простым значениям (78 делится на 2, поскольку заканчивается на четную цифру 8).
3. Разделить две значения вертикальной чертой.
4. Выделить I неполное делимое: 7.
5. По таблице умножения подобрать ближайшее целое (3). При произведении его на делитель должно получиться значение, которое меньше первого неполного делимого (3 * 2 = 6 < 7). Если записать 4, то 4 * 2 = 8 > 7 (вариант не подходит).
6. Записать число, полученное при умножении делителя на подобранное значение, под I неполным делимым. Произвести операцию вычитания (7 — 6 = 1).
7. Результат вычитания (1), который называется остатком, не делится на 2. Следовательно, нужно дописать II неполное делимое (18). Если по какой-то причине, результат делится на делитель, то подобранное значение является неверным.
8. Значение 18 делится на 2, т. е. 18/2 = 9.
9. Результат деления 78 на 2 равен 39.

Операция с остатком

Не во всех случаях результат деления двух чисел является целой величиной. В школьной программе встречается группа примеров, в которых требуется найти остаток, полученный при выполнении операции деления 2 значений (77/3). Алгоритм похож на предыдущий, но имеются некоторые особенности:

1. Два числа записываются, как и в предыдущем случае.
2. Принадлежность к множеству простых чисел не проверяется.
3. Выделить I неполное делимое: 7.
4. Подобрать ближайшее целое число, записав его в результат: 2.
5. Выполнить проверку: 3 * 2 = 6 < 7 (значение подходит).
6. Записать 6 под 7, а затем выполнить операцию вычитания: 7 — 6 = 1. Остаток меньше 3, следовательно, число подобрано правильно.
7. Выполнить подбор множителя для 17: целочисленного значения нет. Следовательно, нужно подобрать ближайшее целое: 5.
8. Произвести проверку: 3 * 5 = 15 < 17.
9. Записать 5 в результат и определить остаток: 17 — 15 = 2.
10. Результат деления 77 на 3 эквивалентен: 25 с остатком 2.

Таким образом, для выполнения операции деления двузначного числа на однозначное нужно знать признаки делимости величин, а также основные алгоритмы деления с остатком и без него.

Калькулятор вычитания столбиком

Данный калькулятор поможет вам выполнить вычитание чисел столбиком. Просто введите уменьшаемое и вычитаемое и нажмите кнопку Вычислить.

Чтобы найти разность методом «вычитание столбиком
» (другими словами, как считать в столбик или столбиком вычитание), необходимо следовать таким шагам:

• поместить вычитаемое под уменьшаемое, записать единицы под единицами, десятки под десятками и т.д.
• вычесть поразрядно.
• если необходимо занять десяток из большего разряда, то над разрядом, в котором заняли, поставить точку. Над разрядом, для которого заняли, поставить 10.
• если в разряде, в котором заняли, стоит 0, тогда занимаем из следующего разряда уменьшаемого и над ним ставим точку. Над разрядом, для которого заняли, поставить 9, т.к. один десяток занят.

Ниже рассмотренные примеры покажут вам как происходит вычитание двухзначных, трехзначных и любых многозначных чисел столбиком.

Вычитание чисел в столбик
очень помогает при вычитании больших чисел (как и сложение в столбик). Лучше всего научиться на примере.

Необходимо записать числа одно под другим таким образом, чтобы крайняя правая цифра 1-го числа стала под крайней правой цифрой 2-го числа. Число, которое больше (уменьшаемое) записываем сверху. Слева между числами ставим знак действия, здесь это «-» (вычитание).

2 — 1 = 1
. То, что у нас получается пишем под чертой:

10 + 3 = 13.

Из 13 вычтем девять.

13 — 9 = 4.

Так как мы заняли десяток у четверки, то она уменьшилось на 1. Для того, чтобы не забыть об этом у нас и стоит точка.

4 — 1 = 3.

Результат:

Порядок вычитания столбиком

Естественно, что будем двигаться справа налево, смотри теорию вычитание столбиком.. Первая цифра справа нумеруется : №1 и так идем справа налево от первой цифры, пока цифры не закончатся. На каждую цифру отдельный пункт, в котором подробно объясняется, что делается в данном столбце по отниманию от верхнего числа нижнего столбиком.

Столбец №1 : верхнее число «312378» и крайняя, правая цифра: «8», которая меньше чем первая цифра «9» справа нижнего числа «». Поэтому… нам нужно занять десяток от верхнего числа соседнего столбца «7» : «7 — 1 = 6». И теперь прибавляем 10 к 8 = 18 и уже от этого числа отнять 9 получим ( и полученное число записываем под 9) :

18 — 9 = 9

Столбец №2 : при вычитании предыдущего столбца(который справа) нам пришлось занять десятку у верхнего числа соседнего столбца слева 312378(теперь мы здесь), поэтому… вместо 7 у нас : 6. И у нас повторяется ситуация предыдущего столбца, когда верхняя цифра меньше нижней 3699… поступаем аналогично… занимаем у верхнего числа соседнего столбца(слева) единицу… и прибавляем к 6 + 10 = 16. Теперь нам нужно опять отнять столбцом(и полученное число 7 записываем под 9)

16 — 9 = 7

Столбец №3 : при вычитании предыдущего столбца(который справа) нам пришлось занять десятку у верхнего числа соседнего столбца слева 312378(теперь мы здесь), поэтому… вместо 3 у нас : 2. И у нас повторяется ситуация предыдущего столбца, когда верхняя цифра меньше нижней 3699… поступаем аналогично… занимаем у верхнего числа соседнего столбца(слева) единицу… и прибавляем к 2 + 10 = 12. Теперь нам нужно опять отнять столбцом(и полученное число 6 записываем под 6)

12 — 6 = 6

Столбец №4 : при вычитании предыдущего столбца(который справа) нам пришлось занять десятку у верхнего числа соседнего столбца слева 312378(теперь мы здесь), поэтому… вместо 2 у нас : 1. И у нас повторяется ситуация предыдущего столбца, когда верхняя цифра меньше нижней 3699… поступаем аналогично… занимаем у верхнего числа соседнего столбца(слева) единицу… и прибавляем к 1 + 10 = 11. Теперь нам нужно опять отнять столбцом(и полученное число 8 записываем под 3)

11 — 3 = 8

Столбец №6. И поскольку цифры второго числа закончились, а верхние ещё остались… 312378 то вам нужно просто поместить даную цифру «3» под черту внизу ничего не делая!

Свойства вычитания

1. Свойство вычитания суммы из числа:

   $a — ( b + c ) = a — b — c.$

   Например, нужно найти значение выражения:

   $123 — ( 23 + 45 ) = 123 — 68 = 55.$

   Однако намного удобнее считать так:

   $123 — ( 23 + 45 ) = 123 — 23 — 45 = 100 — 45 = 55.$

   В этом выражении нужно вычесть сумму из числа, а можно сначала вычесть из уменьшаемого одно слагаемое, а потом из полученной разности вычесть второе слагаемое.

   Например, найдем результат выражения:

   $217 — 33 — 27 = 184 — 27 = 157.$

   Но гораздо легче найти сумму вычитаемых и вычесть ее из уменьшаемого:

   $217 — 33 — 23 = 217 — ( 33 + 27 ) = 217 — 60 = 157.$

2. Свойство вычитания числа из суммы:

   если $c

   если $c

   Рассмотрим три примера с одинаковыми результатами.

   $( 6 + 5 ) — 4=11 — 4=7;$

   $6 + ( 5 — 4 )=6 + 1=7;$

   $( 6 — 4 ) + 5=2 + 5=7.$

   Откуда получаем: $( 6 + 5 ) — 4=6 + ( 5 — 4 )=( 6 — 4 ) + 5.$

   Если нужно вычесть число из суммы, можно вычесть его из любого слагаемого и к полученной разности прибавить другое слагаемое.

   Вычитаемое обязательно должно быть меньше слагаемого, из которого его вычитают, или равным ему.

   Пример 3

   $( 234 + 123 ) — 134=357 — 134=223.$

   Но намного удобнее считать так:

   $( 234 + 123 ) — 134=234 — 134+ 123=100+ 123=223.$

3. Если из числа вычесть нуль, оно не изменится:

   $a — 0 = a.$

   Если из числа вычесть это же число, получим нуль:

   $a — a = 0.$

   Т.к. $9 + 0 = 9$, то по смыслу вычитания имеем:

   

   

   

   

   

   

   

   

   

   

   $9 — 9 = 0$ или $9 — 0 = 9.$

   Результат вычитания удобно находить «в столбик»:

   Рисунок 5.

   Если точкой $C$ разделяется отрезок $AB$, то разность длин отрезков $AB$ и CB$ равна длине отрезка $AC.$

   Рисунок 6.

   Записывается: $AB — CB = AC$ или $AB — AC = CB.$

   Если $AB = 7$ см, а $CB = 4$ см, то $AC = 7 — 4 = 3$ см.

   Пример 4

   Решить уравнение $63 — x = 55.$

   Решение:

   $x = 63 — 55$, откуда $x = 8.$

   Число $8$ называется корнем уравнения $63 — x = 55$, т.к. получаем верное равенство $63 — 8 = 55.$

   Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.

Деление периодических дробей

В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.

Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.

Вычитание десятичных дробей в столбик

Разберем вычитание двух десятичных дробей в столбик на примере. Вычтите 23,5 из 36,96.

• 1) Для удобства вычитания прибавьте к вычитаемому справа 0, чтобы количество знаков после запятой было одинаковым 23,5 = 23,50.
• 2) Запишем десятичные дроби так, чтобы соответствующие цифры были ниже друг друга. 0 до 6, 5 до 9, 3 до 6, 2 до 3.
  

  3	6	.	9	6
  2	3	.	5

• 3) Слева пишем знак — и проводим черту под вычитаемым.
  

  —	3	6	.	9	6
  2	3	.	5

• 4) Вычитание по крупицам справа налево.
  Первые сотые 6-0=6. Пишем 6 под сотыми.
  Тогда десятые 9-5=4. В ответе под десятками пишем 4.
  Тогда единицы 6-3=3. Под единицами пишем 3.
  Тогда десятки 3-2=1. Напишем 1 под десятками.

  —	3	6	.	9	6
  2	3	.	5
  	1	3	.	4	6

Система счисления

Для начала решим, какие числа в математики считаются двузначными. По слову сразу ясно, что это числа, которые содержат два значащих знака. Значащие позиции считаются от единиц вверх, по есть по готовому числу справа налево.

Сначала идут единицы, затем десятки, сотни и так далее. При этом знаки могут распространяться и +влево от единиц в виде десятичных дробей после запятой.

Такая система называется позиционной. Каждая цифра в ней меняет свое значение в зависимости от занимаемой позиции. Например, есть число 23, а есть 32 и это разные числа, которые были записаны при помощи одинаковых цифр. Благодаря такому подходу можно записать любое по своей величине число с помощью всего 9 цифр от 1 до 0.

Отдельно стоит сказать, что значащей считается любая позиция, отличная от нуля. В любом числе незначащих позиций бесконечно много. Мы пишем 23, но понимаем, что в этом числе 0 сотен и тысяч, то есть можно записать его, как 0023.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Правила вычитания в столбик

Чтобы найти разницу между двумя или более числами с любым количеством цифр, вы можете выполнить вычитание столбца. Для этого:

1. Пишем сокращенное в верхней строке.
2. Под ним пишем первое вычитаемое — таким образом, чтобы одинаковые цифры в обоих числах были ниже друг друга (десятки ниже десятков, сотни ниже сотен и так далее)
3. Аналогично добавляем другие вычитаемые, если они есть. В результате образуются столбцы с разными цифрами.
4. Под написанными числами проведите горизонтальную черту, которая будет отделять уменьшаемое и вычитаемое из разницы.
5. Перейдем к вычитанию чисел. Эту процедуру проводят справа налево, отдельно для каждого столбца, а результат записывают под чертой в том же столбце. Здесь есть пара нюансов:
   • Если числа в вычитаемом нельзя вычесть из цифры в уменьшаемом, то из старшего разряда отнимаем десятку, а затем должны учитывать это в дальнейших действиях (см пример 2).
   • Если в уменьшаемом конце стоит ноль, это автоматически означает, что для выполнения вычитания необходимо заимствовать из следующей цифры (см пример 3).
   • Иногда в результате «заимствования» в старшем разряде может не остаться цифр (см пример 4).
   • В редких случаях, когда отчислений много, необходимо брать не один, а сразу два и более десятка (см пример 5).

Если в примере разные дроби…

Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.

Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.

Для того чтобы вычесть одно число из другого, поместим вычитаемое под уменьшаемым, следующим образом: единицы под единицами, десятки под десятками. Для примера, в качестве уменьшаемого возьмем двузначное число, а в качестве вычитаемого – однозначное.

7 – 5 = 2

результатпишем под единицами.

Теперь вычитаем десятки из десятков, но у вычитаемого нет десятков, поэтому опускаем десяток уменьшаемого в ответ.

27 – 5 = 22

Теперь возьмем оба числа двухзначных:

Вычитаем единицы вычитаемого из единиц уменьшаемого:

6 – 4 = 2

результатпишем под единицами

Теперь вычитаем десятки вычитаемого из десятков уменьшаемого:

8 – 3 = 5

результатпишем под десятками.

В результате получаем разность:

86 – 34 = 52

Вычитание с переходом через десяток

Давайте попробуем найти разность следующих чисел:

Вычитаем единицы. Из 7 вычесть 9 нельзя, занимаем один десяток из десятков уменьшаемого. Чтобы не забыть ставим точку над десятками.

17 – 9 = 8

Теперь вычитаем десятки из десятков. У вычитаемого нет десятков, но мы занимали один десяток у уменьшаемого:

2 десятка – 1 десяток = 1 десяток

В результате получаем разность:

27 – 9 = 18

Теперь для примера возьмем трехзначные числа:

Вычитаем единицы. 2
меньше 8
, поэтому занимаем один десяток из десятков уменьшаемого: 2 + 10 = 12 (пишем 10 над единицами). Чтобы не забыть ставим точку над десятками.

12 – 8 = 4

результат пишем под единицами.

Мы занимали один десяток из десятков для единиц, значит в уменьшаемом уже не три десятка, а два (3 десятка – 1 десяток = 2 десятка
).

Два десятка меньше чем шесть, занимаем одну сотню или 10 десятков из сотен (2 десятка + 10 десятков = 12 десятков
пишем 10
над десятками уменьшаемого), а чтоб не забыть ставим точку над сотнями. Вычитаем десятки:

12 десятков – 6 десятков = 6 десятков

результат пишем под десятками.

Мы занимали одну сотню из сотен уменьшаемого для десятков, значит у нас не 9
сотен, а 8
сотен (9 сотен – 1 сотня = 8 сотен
). Вычитаем сотни:

8 сотен – 7 сотен = 1 сотня

. Результат пишем под сотнями.

В результате получаем:

932 – 768 = 164

Усложним задачу. Что делать если в разряде, из которого надо занять десяток, равен нулю? Например:

Начинаем с единиц. 2
меньше 8
, то есть надо занять из десятков. Но у уменьшаемого в десятках , значит, для десятков надо занимать у сотен. В разряде сотен в уменьшаемом тоже , занимаем из тысяч. Чтобы не забыть ставим над тысячами точку.

В сотнях уменьшаемого остается 9
, так как мы занимаем одну сотню для десятков: 10 – 1 = 9
пишем 9

над сотнями.

В десятках тоже остается 9
, так как мы заняли один десяток для единиц: 10 – 1 = 9
пишем 9

над десятками, а над единицами пишем 10

.

Считаем единицы:

12 – 8 = 4

пишем результат под единицами.

В десятках уменьшаемого осталось 9
, считаем:

9 – 6 = 3

пишем результат под десятками.

В сотнях уменьшаемого осталось 9
, у вычитаемого сотен нет, опускаем 9
в ответ под сотни.

В разряде тысяч уменьшаемого была 1
, мы её занимали (точка над тысячами), значит тысяч больше не осталось. В результате получаем:

1002 – 68 = 934

Итак, подведем итог.

Для того чтобы найти разность двух чисел (вычитание столбиком)

:

1. помещаем вычитаемое под уменьшаемым, пишем единицы под единицами, десятки под десятками и так далее.
2. Вычитаем поразрядно.
3. Если надо занять десяток из следующего разряда, то над разрядом, из которого занимали, ставим точку. Над разрядом, для которого занимаем, ставим 10.
4. Если в разряде, из которого занимаем, стоит 0, то для него занимаем из следующего разряда уменьшаемого, над которым ставим точку. Над разрядом, для которого занимали, ставим 9, так как один десяток заняли.

Удобно проводить особым методом, который получил название вычитание столбиком
или вычитание в столбик
. Этот способ вычитания оправдывает свое название, так как уменьшаемое, вычитаемое и разность записываются в столбик. Промежуточные вычисления также проводятся в столбиках, соответствующих разрядам чисел.

Удобство вычитания натуральных чисел столбиком заключается в простоте вычислений. Вычисления сводятся к использованию таблицы сложения и применению свойств вычитания.

Давайте разберемся, как выполняется вычитание столбиком. Процесс вычитания будем рассматривать вместе с решением примеров. Так будет понятнее.

Навигация по странице.

Почему детям сложно научиться делить в столбик?

Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.

Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.

Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.

Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?

Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.

Я уже писала о том, Эта статья может стать для вас полезной.

Как объяснить ребенку деление в столбик: алгоритм решения

Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:

Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).

213:3213 — делимое3 — делитель

Записать делимое — «уголок» — делитель.

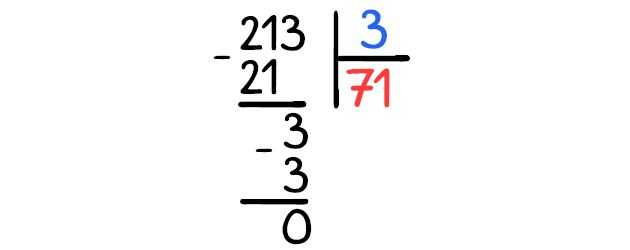
Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.

Рассуждаем так: 2 не делится на 3, значит — берем 21.

Определить, сколько раз делитель «помещается» в выбранной части.

21 разделить на 3 — берем по 7.

Умножить делитель на выбранное число, результат записать под «уголком».

7 умножить на 3 — получаем 21. Записываем.

Найти разницу (остаток).

На этом этапе рассуждений научите ребенка проверять себя

Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз

Повторить действия, пока в остатке не окажется 0.

Калькулятор вычитания столбиком

Данный калькулятор поможет вам выполнить вычитание чисел столбиком. Просто введите уменьшаемое и вычитаемое и нажмите кнопку Вычислить.

В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.

Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.

Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.

Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.

Определение вычитания

Вычесть значит отнять одно число от другого.

Вычитание есть такое действие, в котором отнимают меньшее число от большего. При вычитании целых чисел большее число уменьшается на столько единиц, сколько их содержится в меньшем. Вычесть одно число из другого значит убавить одно число другим, поэтому вычитание есть действие обратное сложению.

В вычитании два данных числа называются уменьшаемым и вычитаемым, а искомое — разностью.

Уменьшаемым называют большее число, от которого отнимают другое. Оно уменьшается от вычитания.

Вычитаемым называют меньшее число, которое отнимают от большего.

Разностью называют вывод, полученный от вычитания. Разность определяет, чем одно число больше другого или показывает разницу между двумя числами.

Знак вычитания. Действие вычитания обозначается знаком — (минус).

Как объяснить ребенку деление двузначного числа на однозначное не в столбик?

Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?

Возьмем для примера 72:3.

Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3: 72=30+30+12.

Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3. Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).

72:3=24Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.

После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.

Вычитание чисел

Вычитание чисел легко освоить любому первокласснику. Например, из 6 нужно вычесть 5. 6-5=1, 6 больше числа 5 на единицу, значит, и ответ будет единицей. Можно для проверки произвести сложение 1+5=6. Если вы не знакомы со сложением, то можете прочитать нашу .

Большое число делится на части, возьмем число 1234, а в нем: 4-единицы, 3-десятки, 2-сотни, 1-тысячи. Если вычитать единицы, то все легко и просто. Но допустим пример: 14-7. В числе 14: 1-десяток, а 4- единицы. 1 десяток – 10 единиц. Тогда получаем 10+4-7, сделаем так: 10-7+4, 10 – 7 =3, а 3+4=7. Ответ найден верно!

Рассмотрим пример 23 -16. Первое число 2 десятка и 3 единицы, а второе 1 десяток и 6 единиц. Представим число 23 как 10+10+3, а 16 как 10+6, тогда представим 23-16 как 10+10+3-10-6. Тогда 10-10=0, останется 10+3-6, 10-6=4, тогда 4+3=7. Ответ найден!

Аналогично делается с сотнями и тысячами