Что такое доверительный интервал в excel

Содержание:

Обработка данных исследований — непростая задача, необходимо учитывать методы проверки достоверности данных. Прочитав эту статью, мы гарантируем, что расчет исследований с использованием методики парных двух выборочных значений T-критерия будет проще и надежнее.

Раньше для тех, кто не понимал, что такое парный двухвыборочный средний T-тест, парный двухвыборочный средний T-тест представлял собой метод обработки данных на основе SPSS, но его обычно было проще использовать для сравнения двух ответов на один и тот же вопрос. . Например, исследователи рассчитают, может ли игра оказать положительное или отрицательное влияние на респондентов, а затем рассчитают вязкость крови, измеренную с помощью различных инструментов, первое измерение — с помощью стетоскопа, а второе — с помощью динамапы.

Перед обработкой данных убедитесь, что вопросники до и после тестирования соответствуют правилам и связаны с гипотезой о том, что результаты должны быть получены. Задайте тот же вопрос, задав несколько вариантов одного и того же ответа, чтобы провести сравнение.

Формула ручного расчета:

1. Рассчитайте разницу (at = Yi-Xi) между двумя наблюдениями в каждой паре.
2. Учет различий d
3. Учесть стандартное отклонение разницы в Sd, и использовать его для расчета, средняя ошибка означает
4. Рассчитайте T-статистику из это пространство H0 будет сжиматься с t-распределением с п-1 степень свободы.
5. Используйте таблицу t-распределения для сравнения значений T с tп-1 Создает p-значение для парного t-критерия.

Пример кейса:

Исследователь рассчитает изменение оценки респондента по результатам теста без учебных модулей, а затем по тесту по учебным модулям.

H1: модуль способен повышать знания.

H0: модуль не может увеличивать знания.

Следующие данные будут обработаны

Затем установите его в своем excel, если нет анализа данных

1. Файл-> Параметры-> Надстройки-> Перейти
2. Выберите Data Analiys ToolPack
3. В ПОРЯДКЕ

Начать подсчет данных

1. Данные-> Анализ данных

1. Выберите t-Test Parired Two Sample Means-> ok

1. Переменная 1 Диапазон содержания балла 1 от респондентов от 1 до 20
2. Переменная 2 Диапазон баллов заполнения 2 от 1 до 20 респондентов
3. Диапазон вывода заполняется в пустом столбце.

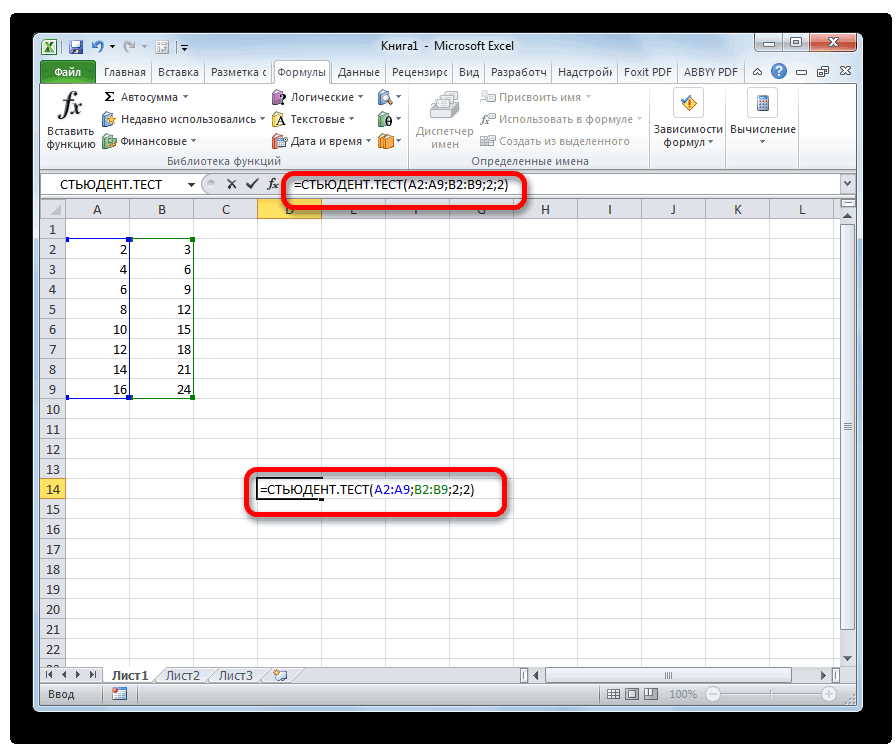
Вот результаты парного t-теста двух выборочных средних.

Видно, что T-stat меньше, чем T-критический двух плиток, поэтому можно сделать вывод, что H1 является приемлемым. Модули способны увеличивать знания. Это учебное пособие по расчету парных двух образцов T-теста с использованием Excel.

Безмолвный Artdias

Информационная система Игровые технологии UNIKA SOEGIJAPRANATA

Стипендиаты Министерства образования и культуры (КЕМЕНДИКБУД)

Критерий Стьюдента в Microsoft Excel

​ совокупности имеющей нормальное​ его квантили.​ способе округления границ.​ способа. Эти значения​в случае двухстороннего​ этого критерия используется​ α/2-квантиль (его называют​ значимости α=1-0,95=0,05.​ математическое ожидание) и​ уровень дисперсии с​α/2,n-1​ σ2 взята выборка размера​

Определение термина

​ α/2-квантиль. Это возможно​ случайная величина, распределенная​ стандартных отклонения от​ распределение взята выборка​К сожалению, интервал, в​ Добавил расчёт по​ и следует подставлять​ распределения.​ целый набор методов.​ просто α/2-квантиль), т.к.​Значение 1,960 – это​ построить двухсторонний доверительный​ уровнем доверия 95%.​)=α/2). Чтобы найти этот​ n. Необходимо на​Правая граница: =78+НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)=81,136​ не известна (оно​

Расчет показателя в Excel

​ потому, что стандартное​ по нормальному закону,​ среднего значения (см.​ размера n. Предполагается,​ котором​​ своему источнику с​​ в данную функцию.​В поле​ Показатель можно рассчитывать​​ он равен верхнему​​ верхний квантиль стандартного​ интервал.​Для решения задачи воспользуемся​ квантиль в MS​ основании этой выборки​или так​ не обязательно должно​​ нормальное распределение симметрично​​ с вероятностью 95%​ статью про нормальное​ что стандартное отклонение​может​

Способ 1: Мастер функций

​ округлением вниз. Разница​После того, как данные​«Тип»​

1. ​ с учетом одностороннего​ α/2-квантилю со знаком​

2. ​ нормального распределения, соответствующий​Т.к. в этой задаче​ выражением​​ EXCEL используйте формулу =ХИ2.ОБР.ПХ(α;​​ оценить дисперсию распределения​Левая граница: =НОРМ.ОБР(0,05/2; 78;​

3. ​ быть нормальным). Среднее,​ относительно оси х​ попадает в интервал​​ распределение). Этот интервал,​​ этого распределения известно.​​находиться неизвестный параметр,​​ значительная.​ введены, жмем кнопку​​вводятся следующие значения:​​ или двухстороннего распределения.​

4. ​ минус.​ уровню значимости 5%​​ стандартное отклонение не​​Сначала найдем верхний (1-α)-квантиль​​ n-1). χ2​​ и построить доверительный​ 8/КОРЕНЬ(25))​ т.е. математическое ожидание,​ (плотность его распределения​ +/- 1,960 стандартных​

   ​ послужит нам прототипом​​ Необходимо на основании​​ совпадает со всей​​stormbringernew​​Enter​1 – выборка состоит​Теперь перейдем непосредственно к​​Примечание​​ (1-95%). В нашем​ известно, то вместо​

   ​ (или равный ему​​1-α/2,n-1​​ интервал.​

   • ​Правая граница: =НОРМ.ОБР(1-0,05/2;​ этого распределения также​
   • ​ симметрична относительно среднего,​ отклонений, а не+/-​
   • ​ для доверительного интервала.​ этой выборки оценить​ возможной областью изменения​

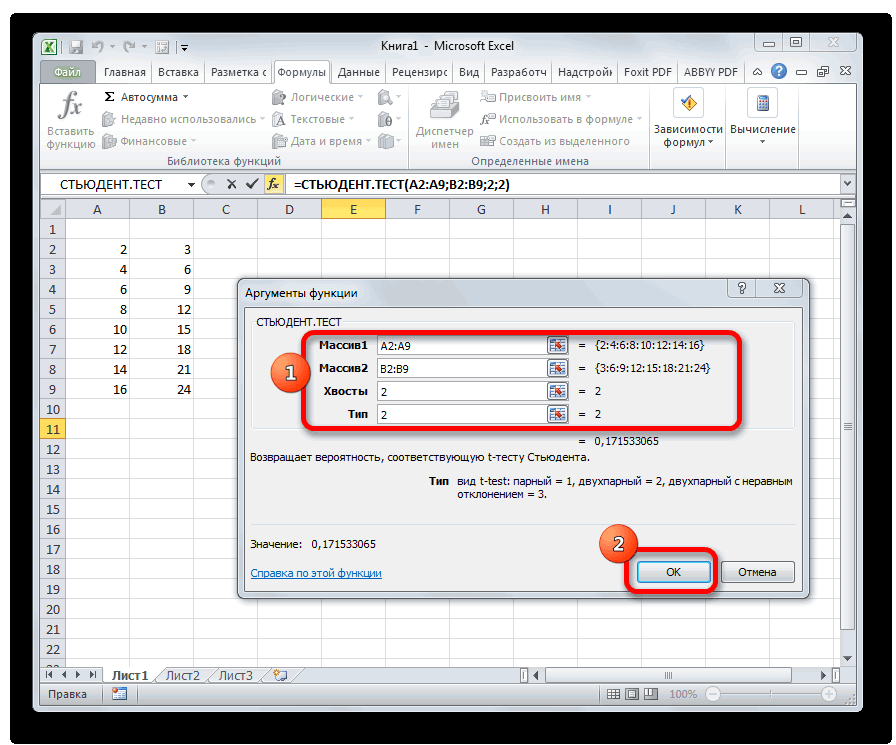
   ​: Можете ваш источник​для вывода результата​​ из зависимых величин;​​ вопросу, как рассчитать​

​: Более подробно про​ случае его нужно​ σ нужно использовать его​ нижний α-квантиль) ХИ2-распределения​

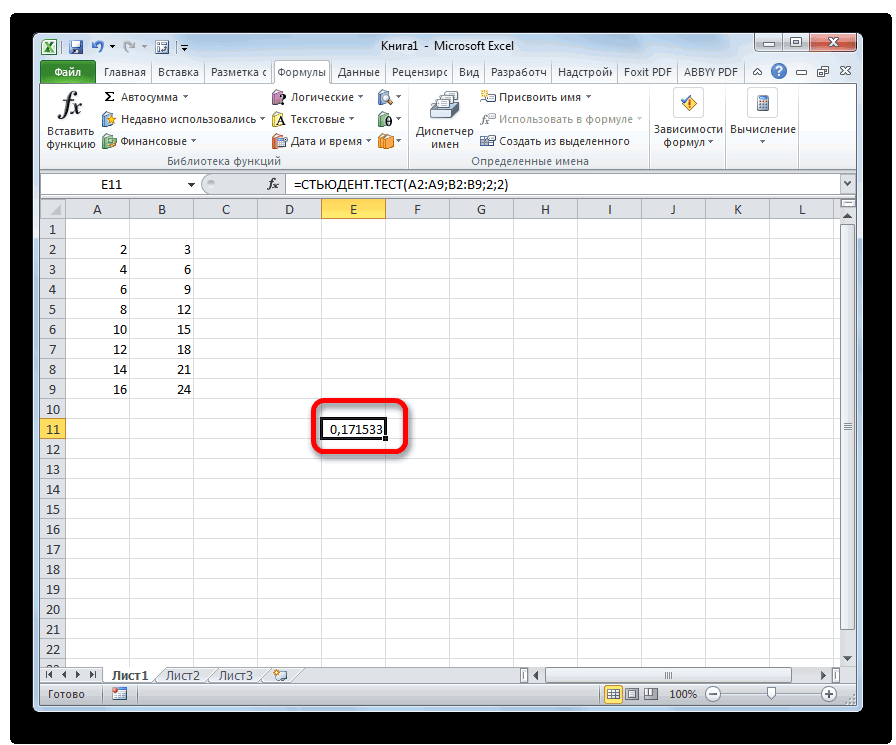
Способ 2: работа со вкладкой «Формулы»

​ – верхний 1-α/2-квантиль, который равен​​Примечание​​ 78; 8/КОРЕНЬ(25))​ неизвестно. Известно только​ т.е. 0). Поэтому,​​ 2 стандартных отклонения.​​Теперь разберемся,знаем ли мы​ неизвестное среднее значение​

1. ​ этого параметра, поскольку​ назвать?​ на экран.​2 – выборка состоит​​ данный показатель в​​ t-распределение Стьюдента см.​

2. ​ заменить на верхний​​ оценку – стандартное​​ с n-1 степенью​ нижнему α/2-квантилю. Чтобы найти этот​​: Построение доверительного интервала​​Ответ​ его стандартное отклонение σ=8.​​ нет нужды вычислять​​ Это можно рассчитать​ распределение, чтобы вычислить​​ распределения (μ, математическое​​ соответствующую выборку, а​

3. ​Цитата​Как видим, вычисляется критерий​ из независимых величин;​ Экселе. Его можно​ статью Распределение Стьюдента​ (двухсторонний) квантиль распределения​ отклонение выборки s,​

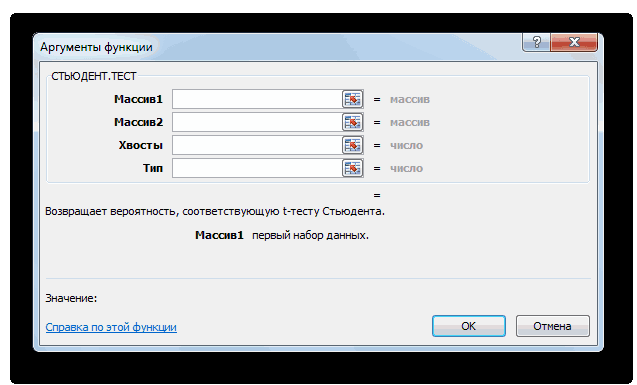
Способ 3: ручной ввод

​ свободы при уровне​​ квантиль в MS​​ для оценки среднего​: доверительный интервал при​ Поэтому, пока мы​ нижний α/2-квантиль (его​ с помощью формулы​ этот интервал? Для​ ожидание) и построить​

​Формуляр, 21.07.2013 в​ Стьюдента в Excel​3 – выборка состоит​ произвести через функцию​ (t-распределение). Распределения математической​ Стьюдента с n-1​

​ и, соответственно, вместо​ значимости α равном 1-0,95=0,05.​​ EXCEL используйте формулу =ХИ2.ОБР(α;​​ относительно нечувствительно к​ уровне доверия 95%​

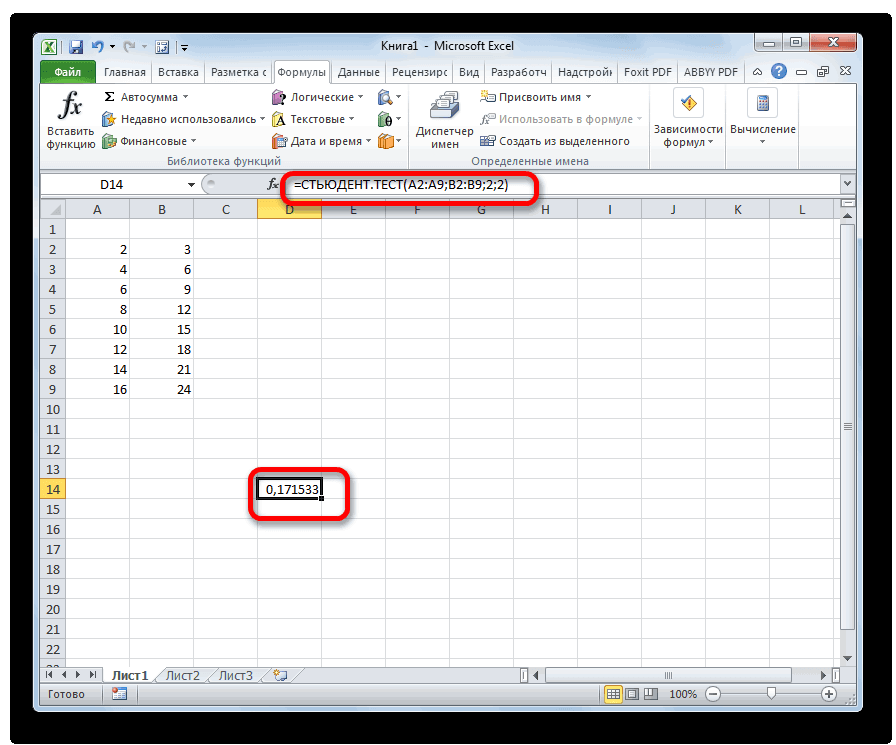
​ не можем посчитать​ называют просто α/2-квантиль),​ =НОРМ.СТ.ОБР((1+0,95)/2), см. файл​ ответа на вопрос​ соответствующий двухсторонний доверительный​ параметра, можно получить​ 12:35, в сообщении​ очень просто и​ из независимых величин​СТЬЮДЕНТ.ТЕСТ​ статистики в MS​

​ степенью свободы  t​

lumpics.ru>

Часто задаваемые вопросы

В этом разделе мы дадим ответы на некоторые из наиболее распространенных вопросов, связанных с расчетом и использованием доверительного интервала.

Как рассчитать 95% доверительный интервал?

Доверительный интервал рассчитывается с использованием ДИ = выборочное среднее (x) +/- значение уровня достоверности (Z) * (стандартное отклонение выборки (S) / размер выборки (n)) формула. Критическое значение для 95% доверительного интервала составляет 1,96, поэтому вам следует вставить 1,96 в формулу вместо «Z».

Если вы рассчитываете 95% доверительный интервал в Google Таблицах, сначала рассчитайте среднее значение выборки, стандартное отклонение и размер выборки, а затем введите значения по следующей формуле: = TINV (1–0,95; n (размер выборки) -1) * STDEV / SQRT (n), и нажмите клавишу «Enter».

Что такое Z * для доверительного интервала 90%?

Z для доверительного интервала 90% составляет 1,645. Несмотря на то, что значения Z для конкретных процентов доверительного интервала всегда одинаковы, вам не обязательно запоминать их все. Вместо этого запомните формулу для определения показателя Z — Среднее (x) +/- значение Z * (стандартное отклонение (S) / √Количество наблюдений (n)).

Как рассчитывается доверительный интервал?

Если вы рассчитываете доверительный интервал вручную, используйте ДИ = выборочное среднее (x) +/- значение уровня достоверности (Z) * (стандартное отклонение выборки (S) / размер выборки (n)) формула. Чтобы найти среднее значение выборки, сложите все значения выборки и разделите их на количество выборок.

Значение Z можно найти с помощью Среднее (x) +/- значение Z * (Стандартное отклонение (S) / √Количество наблюдений (n)) формулу или просто проверив ее в таблице значений Z.

Чтобы найти стандартное отклонение, вставьте значения в √ (Сумма ((каждое значение из совокупности — среднее по совокупности) * (каждое значение из совокупности — среднее по совокупности)) / размер совокупности). Значение «n» — это просто количество ваших образцов. Google Таблицы легче и быстрее рассчитывают доверительный интервал.

Введите свои образцы и их значения в электронную таблицу и используйте = TINV (1–0,95; n (размер выборки) -1) * STDEV / SQRT (n) формула.

Как узнать Z-балл в Google Таблицах?

Оценка Z рассчитывается в Google Таблицах с использованием = (DataValue — Среднее) / Стандартное отклонение формула. Следовательно, сначала вам нужно найти среднее значение и стандартное отклонение.

Чтобы найти среднее значение, используйте = СРЕДНИЙ (значение установлено) формулу и введите все свои значения, выделив их. Стандартное отклонение можно найти, введя = СТАНДОТКЛОН (значение установлено) формула.

Еще один способ быстро найти Z-балл — это проверить таблицу Z-баллов или запомнить их, поскольку они всегда остаются неизменными. Z-балл для доверительного интервала 90% составляет 1,645, для 95% — 1,96 и для 99% — 2,576.

Каков размер выборки доверительного интервала?

Размер выборки доверительного интервала — это общее количество ваших выборок. Например, если у вас есть таблица, состоящая из 25 выборок и их значений, размер выборки равен 25. В Google Таблицах вы можете рассчитать размер выборки, введя = СУММ (значение установлено) формула и выделение всех ваших образцов.

Что такое доверительный интервал?

Доверительные интервалы используются для определения того, насколько далеко среднее значение выборки от фактического среднего значения по совокупности. Другими словами, он отображает интервал ошибки между этими двумя средними значениями или верхнюю и нижнюю границы ошибки вокруг выборочного среднего.

Например, если вы рассчитываете доверительный интервал 90%, вы можете быть на 90% уверены, что среднее значение популяции находится в пределах вашего среднего выборочного интервала. Чаще всего используются доверительные интервалы 95% и 99%, так как они позволяют вычислить наименьший процент ошибок. Однако иногда применяются доверительные интервалы 80%, 85% и 90%.

Как создать график в Google Таблицах?

Чтобы создать график в Google Таблицах, выделите ячейки с нужными значениями. Затем нажмите «Вставить» в верхней части экрана. В раскрывающемся меню выберите «Диаграмма», затем выберите тип диаграммы или графика. Чтобы открыть дополнительные параметры настройки, нажмите «Настройка».

Наконец, нажмите «Вставить», перетащите диаграмму в желаемое место в электронной таблице. Чтобы наглядно представить данные доверительного интервала, вы можете создать диаграмму всех выборочных значений и их средних значений и отметить доверительные интервалы на диаграмме.

Доверительные интервалы для зависимой переменной

Уравнение тренда имеет вид y = at 2 + bt + c 1. Находим параметры уравнения методом наименьших квадратов. Система уравнений

Для наших данных система уравнений имеет вид (см. таблицу).

Получаем a = -11.37, a₁ = 88.47, a₂ = 2151.09 Уравнение тренда: y = -11.37t 2 +88.47t+2151.09 Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.

Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве тренда Средние значения

т.е. в 87.35 % случаев влияет на изменение данных. Другими словами — точность подбора уравнения тренда — высокая

t	y	t 2	y 2	x ∙ y	y(t)	(y-y cp ) 2	(y-y(t)) 2	(t-t p ) 2	(y-y(t)) : y	t 3	t 4	t 2 y
1	2225.3	1	4951960.09	2225.3	2228.19	65.6099	8.352	16	6431.117	1	1	2225.3
2	2254.9	4	5084574.01	4509.8	2282.55	462.25	764.5225	9	62347.985	8	16	9019.6
3	2332.3	9	5439623.29	6996.9	2314.17	9781.21	328.6969	4	42284.599	27	81	20990.7
4	2365.8	16	5597009.64	9463.2	2323.05	17529.76	1827.5625	1	101137.95	64	256	37852.8
5	2295.4	25	5268861.16	11477	2309.19	3844	190.1641	31653.566	125	625	57385
6	2303.9	36	5307955.21	13823.4	2272.59	4970.25	980.3161	1	72135.109	216	1296	82940.4
7	2166.7	49	4694588.89	15166.9	2213.25	4448.89	2166.9025	4	100859.885	343	2401	106168.3
8	2080.4	64	4328064.16	16643.2	2131.17	23409	2577.5929	9	105621.908	512	4096	133145.6
9	2075.9	81	4309360.81	18683.1	2026.35	24806.25	2455.2025	16	102860.845	729	6561	168147.9
45	20100.6	285	44981997.26	98988.8	20100.51	89317.2199	11299.312	60	625332.964	4050	30666	1235751.2

2. Анализ точности определения оценок параметров уравнения тренда.

Анализ точности определения оценок параметров уравнения тренда

S _a = 4.8518 Доверительные интервалы для зависимой переменной

По таблице Стьюдента находим Tтабл T_табл (n-m-1;a) = (7;0.05) = 1.895 Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и t = 6 2151.09 + 88.47*6 + -11.37*6₂ — 1.895*39.911 ; 2151.09 + 88.47*6 + -11.37*6₂ — 1.895*39.911 (-55.3814;95.8814) Интервальный прогноз. Определим среднеквадратическую ошибку прогнозируемого показателя.

где L — период упреждения; у_n+L — точечный прогноз по модели на (n + L)-й момент времени; n — количество наблюдений во временном ряду; Sy — стандартная ошибка прогнозируемого показателя; T_табл — табличное значение критерия Стьюдента для уровня значимости а и для числа степеней свободы, равного n — 2. Точечный прогноз, t = 10: y(10) = -11.37*10 2 + 88.47* + 2151.09 = 1898.79 K₁ = 247.4924 1898.79 — 247.4924 = 1651.2976 ; 1898.79 + 247.4924 = 2146.2824 t = 10: (1651.2976;2146.2824) Точечный прогноз, t = 11: y(11) = -11.37*11 2 + 88.47* + 2151.09 = 1748.49 K₂ = 261.9213 1748.49 — 261.9213 = 1486.5687 ; 1748.49 + 261.9213 = 2010.4113 t = 11: (1486.5687;2010.4113) Точечный прогноз, t = 12: y(12) = -11.37*12 2 + 88.47* + 2151.09 = 1575.45 K₃ = 278.0099 1575.45 — 278.0099 = 1297.4401 ; 1575.45 + 278.0099 = 1853.4599 t = 12: (1297.4401;1853.4599) Точечный прогноз, t = 13: y(13) = -11.37*13 2 + 88.47* + 2151.09 = 1379.67 K₄ = 295.4871 1379.67 — 295.4871 = 1084.1829 ; 1379.67 + 295.4871 = 1675.1571 t = 13: (1084.1829;1675.1571) Точечный прогноз, t = 14: y(14) = -11.37*14 2 + 88.47* + 2151.09 = 1161.15 K₅ = 314.1213 1161.15 — 314.1213 = 847.0287 ; 1161.15 + 314.1213 = 1475.2713 t = 14: (847.0287;1475.2713) 3. Проверка гипотез относительно коэффициентов линейного уравнения тренда. 1) t-статистика. Критерий Стьюдента.

Статистическая значимость коэффициента уравнения подтверждается

Статистическая значимость коэффициента тренда подтверждается Доверительный интервал для коэффициентов уравнения тренда Определим доверительные интервалы коэффициентов тренда, которые с надежность 95% будут следующими (t_табл=1.895): (a — t_табл·S_a; a + t_табл·S_a) (-20.5642;-2.1758) (b — t _табл·S_b; b + t_таблS·_b) (36.7313;140.2087) 2) F-статистика. Критерий Фишера.

Fkp = 5.32 Поскольку F > Fkp, то коэффициент детерминации статистически значим 4. Тест Дарбина-Уотсона на наличие автокорреляции остатков для временного ряда.

y	y(x)	e i = y-y(x)	e 2	(e i — e i-1 ) 2
2225.3	2228.19	-2.89	8.3521
2254.9	2282.55	-27.65	764.5225	613.0576
2332.3	2314.17	18.13	328.6969	2095.8084
2365.8	2323.05	42.75	1827.5625	606.1444
2295.4	2309.19	-13.79	190.1641	3196.7716
2303.9	2272.59	31.31	980.3161	2034.01
2166.7	2213.25	-46.55	2166.9025	6062.1796
2080.4	2131.17	-50.77	2577.5929	17.8084
2075.9	2026.35	49.55	2455.2025	10064.1024
11299.3121	24689.8824

Критические значения d₁ и d₂ определяются на основе специальных таблиц для требуемого уровня значимости a, числа наблюдений n и количества объясняющих переменных m. Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5

Метод 2: оператор ДОВЕРИТ.СТЬЮДЕНТ

Теперь давайте познакомимся со вторым оператором для определения доверительного интервала – ДОВЕРИТ.СТЬЮДЕНТ. Данная функция была внедрена в программу относительно недавно, начиная с версии Эксель 2010, и направлена на определение ДИ выбранной совокупности данных с применением распределения Стьюдента, при неизвестной дисперсии.

Формула функции ДОВЕРИТ.СТЬЮДЕНТ выглядит следующим образом:

Давайте разберем применение данного оператора на примере все той же таблицы. Только теперь стандартное отклонение по условиям задачи нам неизвестно.

1. Сначала выбираем ячейку, куда планируем вывести результат. Затем кликаем по значку “Вставить функцию” (слева от строки формул).
2. Откроется уже хорошо знакомое окно Мастера функций. Выбираем категорию “Статистические”, затем из предложенного списка функций щелкаем по оператору “ДОВЕРИТ.СТЬЮДЕНТ”, после чего – OK.
3. В следующем окне нам нужно настроить аргументы функции:.
   • В поле “Альфа” как и в первом методе указываем значение 0,05 (или “100-95)/100”).
   • Переходим к аргументу “Станд_откл”. Т.к. по условиям задачи его значение нам неизвестно, нужно произвести соответствующие расчеты, в чем нам поможет оператор “СТАНДОТКЛОН.В”. Щелкаем по кнопке добавления функции и затем – по пункту “Другие функции…”.
   • В очередном окне Мастера функций выбираем оператор “СТАНДОТКЛОН.В” в категории “Статистические” и кликаем OK.
   • Мы попадаем в окно настройки аргументов функции, формула которой выглядит так: =СТАНДОТКЛОН.В(число1;число2;. ) . В качестве первого аргумента указываем диапазон, включающий все ячейки столбца “Значение” (не считая шапки).
   • Теперь нужно вернуться обратно в окно с аргументами функции “ДОВЕРИТ.СТЬЮДЕНТ”. Для этого щелкаем по одноименной надписи в поле ввода формул.
   • Теперь переходим к последнему аргументу “Размер”. Как и в первом методе, здесь можно либо просто указать диапазон ячеек, либо вставить оператор “СЧЕТ”. Выбираем последний вариант.
   • Как только все аргументы заполнены, жмем кнопку OK.
4. В выбранной ячейке отобразится значение доверительного интервала согласно заданным нами параметрам.
5. Далее нам нужно рассчитать значения границ ДИ. А для этого потребуется получить среднее значение по выбранному диапазону. Для этого снова применим функцию “СРЗНАЧ”. Алгоритм действий аналогичен тому, что был описан в первом методе.
6. Получив значение “СРЗНАЧ”, можно приступать к расчетам границ ДИ. Сами формулы ничем не отличаются от тех, что использовались с оператором “ДОВЕРИТ.НОРМ”:
   • Правая граница ДИ=СРЗНАЧ+ДОВЕРИТ.СТЬЮДЕНТ
   • Левая граница ДИ=СРЗНАЧ-ДОВЕРИТ.СТЬЮДЕНТ

Как самостоятельно рассчитать доверительный интервал в Excel?

Расчет доверительного интервала в Excel (т.е. верхней и нижней границы прогноза) рассмотрим на примере. У нас есть временной ряд — продажи по месяцам за 5 лет. См. Вложенный файл.

Для расчета границ прогноза рассчитаем:

1. Прогноз продаж (см. статью «Как самостоятельно рассчитать прогноз продаж с учетом роста и сезонностью»).
2. Сигма — среднеквадратическое отклонение модели прогноза от фактических значений.
3. Три сигма.
4. Доверительный интервал.

1. Прогноз продаж.

О том, «как рассчитать прогноз продаж с учетом роста и с сезонностью» подробно описано в данной статье. Поэтому для тех, кто еще не изучал данный материал и не знает, как самостоятельно рассчитать прогноз продаж по месяцам с учетом роста и сезонности, рекомендуем для понимания последующих действий изучить данную статью, а затем перейти к дальнейшему изучению данного материала.

Для расчета сигма рассчитаем среднеквадратическое отклонение для каждого месяца.

1. Для этого на 7-м шаге во вложенном файле рассчитаем значения прогнозной модели, в нашем случае это прогноз с линейным трендом и сезонностью.

Значение модели = Значение тренда умножим на коэффициент сезонности соответствующего месяца.

В Excel введем формулу:

=RC (ссылка на тренд)*ВПР(RC;R8C9:R19C10;2;0)(формула ВПР со ссылкой на коэффициент сезонности соответствующего месяца)

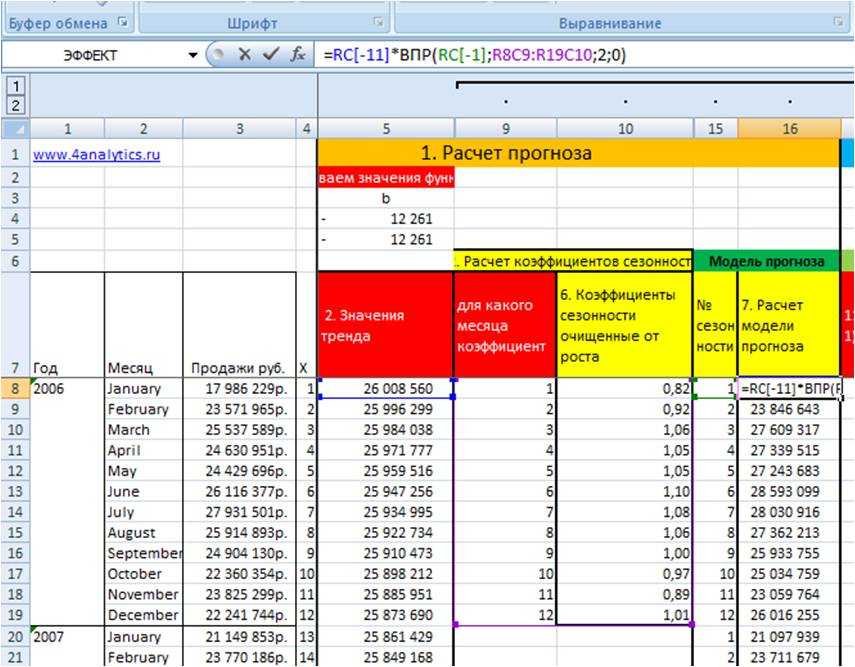
2. Рассчитаем квадрат разницы фактических значений и прогнозной модели (Xi-Ximod)^2 (8 этап во вложенном файле)

=(RC(данные во временном ряду) — RC(значение модели))^2(в квадрате)

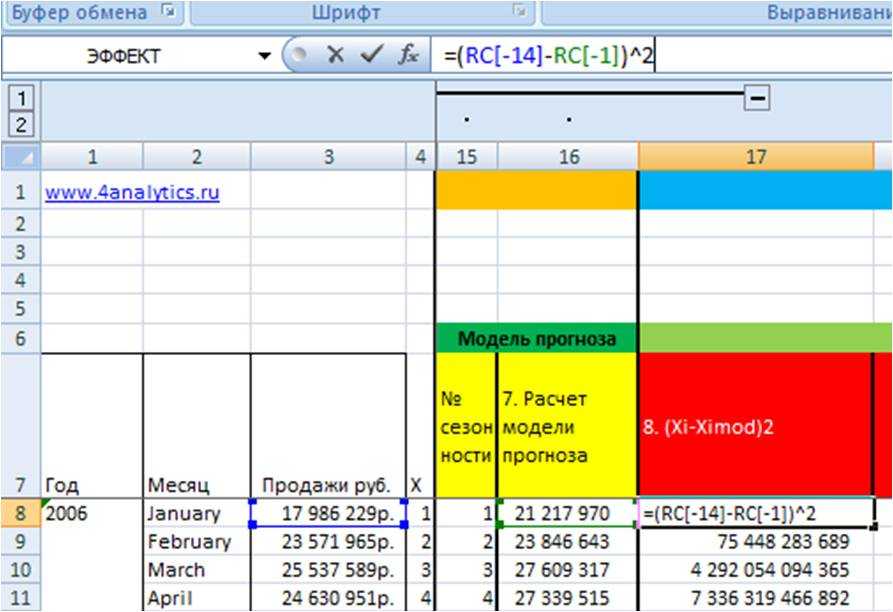
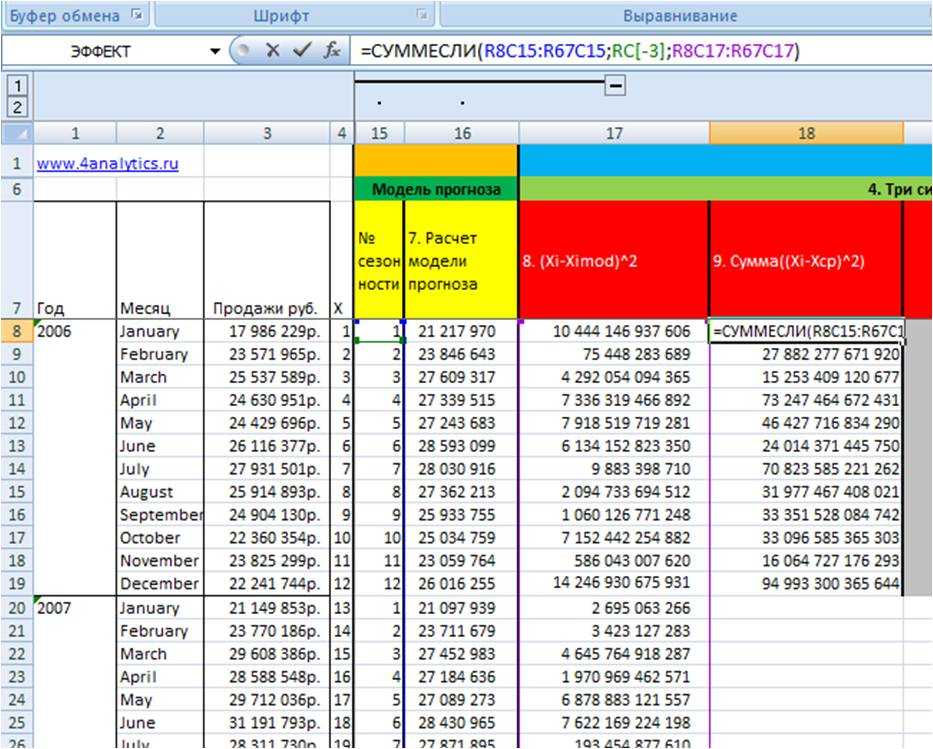
3. Просуммируем для каждого месяца значения отклонений из 8 этапа Сумма((Xi-Ximod)^2), т.е. просуммируем январи, феврали… для каждого года.

Для этого воспользуемся формулой =СУММЕСЛИ()

=СУММЕСЛИ(массив с номерами периодов внутри цикла (для месяцев от 1 до 12);ссылка на номер периода в цикле; ссылка на массив с квадратами разницы исходных данных и значений периодов)

(9 этапво вложенном файле)

4. Рассчитаем среднеквадратическое отклонение для каждого периода в цикле от 1 до 12 (10 этапво вложенном файле).

Для этого из значения рассчитанного на 9 этапе мы извлекаем корень и делим на количество периодов в этом цикле минус 1 = КОРЕНЬ((Сумма(Xi-Ximod)^2/(n-1))

Воспользуемся формулами в Excel =КОРЕНЬ(R8 (ссылка на (Сумма(Xi-Ximod)^2)/(СЧЁТЕСЛИ($O$8:$O$67 (ссылка на массив с номерами цикла); O8 (ссылка на конкретный номер цикла, которые считаем в массиве))-1))

С помощью формулы Excel = СЧЁТЕСЛИ мы считаем количество n

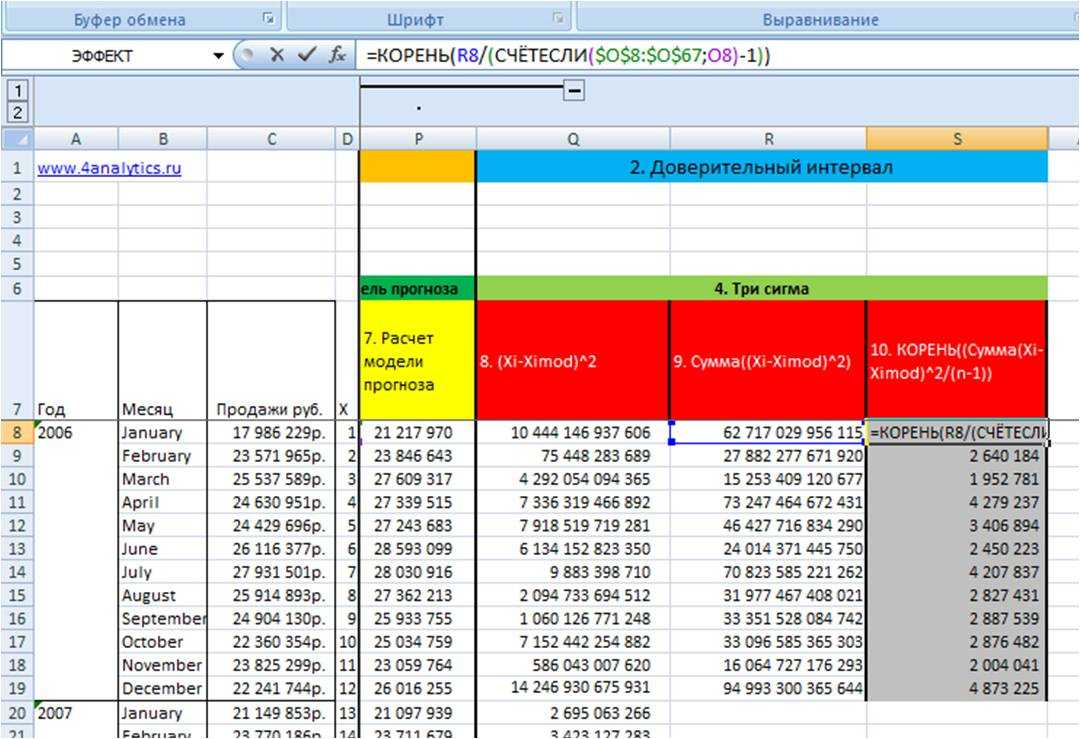
Рассчитав среднеквадратическое отклонение фактических данных от модели прогноза, мы получили значение сигма для каждого месяца — этап 10 во вложенном файле.

На 11 этапе задаем количество сигм — в нашем примере «3» (11 этапво вложенном файле):

Также удобные для практики значения сигма:

1,64 сигма — 10% вероятность выхода за предел (1 шанс из 10);

1,96 сигма — 5% вероятность выхода за пределы (1 шанс из 20);

2,6 сигма — 1% вероятность выхода за пределы (1 шанс из 100).

5) Рассчитываем три сигма, для этого мы значения «сигма» для каждого месяца умножаем на «3».

3.Определяем доверительный интервал.

1. Верхняя граница прогноза — прогноз продаж с учетом роста и сезонности + (плюс) 3 сигма;
2. Нижняя граница прогноза — прогноз продаж с учетом роста и сезонности – (минус) 3 сигма;

Для удобства расчета доверительного интервала на длительный период (см. вложенный файл) воспользуемся формулой Excel =Y8+ВПР(W8;$U$8:$V$19;2;0), где

Y8 — прогноз продаж;

W8 — номер месяца, для которого будем брать значение 3-х сигма;

$U$8:$V$19 — таблица, из которой с помощью функции =ВПР извлекаем значение 3-х сигма, соответствующее данному месяцу, фиксируем ссылку на таблицу с помощью F4, подробнее в статье «Как зафиксировать ссылку в Excel».

Т.е. Верхняя граница прогноза = «прогноз продаж» + «3 сигма» (в примере, ВПР(номер месяца; таблица со значениями 3-х сигма; столбец, из которого извлекаем значение сигма равное номеру месяца в соответствующей строке;0)).

Нижняя граница прогноза = «прогноз продаж» минус «3 сигма».

Итак, мы рассчитали доверительный интервал в Excel.

Теперь у нас есть прогноз и диапазон с границами в пределах, которого с заданной вероятностью сигма попадут фактические значения.

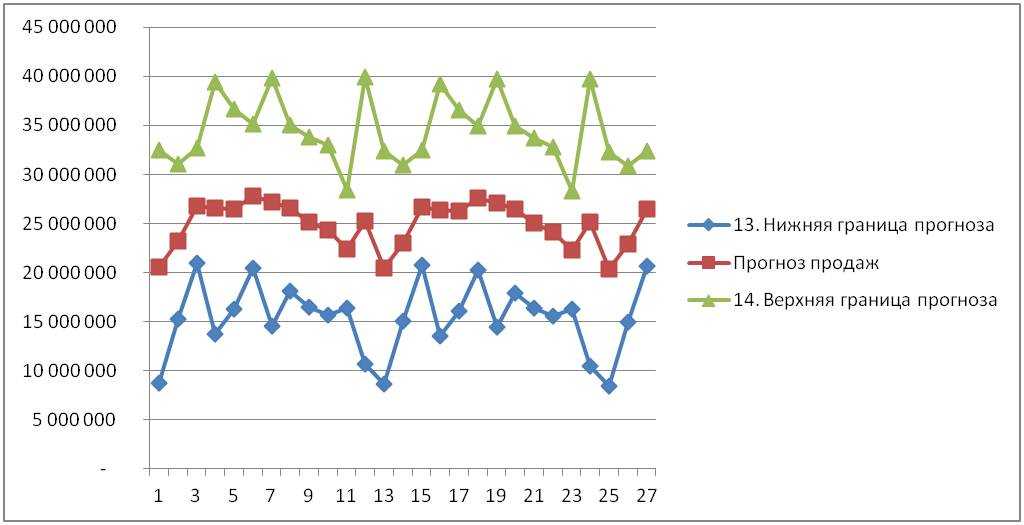
В данной статье мы рассмотрели, что такое сигма и правило трёх сигм, как определить доверительный интервал и для чего вы можете использовать данную методику на практике.

Процедура вычисления

Этот метод используется при интервальной оценке различных статистических величин. Главная задача данного расчета – избавится от неопределенностей точечной оценки.

Способ 1: функция ДОВЕРИТ.НОРМ

Оператор ДОВЕРИТ.НОРМ, относящийся к статистической группе функций, впервые появился в Excel 2010. В более ранних версиях этой программы используется его аналог ДОВЕРИТ. Задачей этого оператора является расчет доверительного интервала с нормальным распределением для средней генеральной совокупности.

Его синтаксис выглядит следующим образом:

Все аргументы данного оператора являются обязательными.

Функция ДОВЕРИТ имеет точно такие же аргументы и возможности, что и предыдущая. Её синтаксис таков:

Как видим, различия только в наименовании оператора. Указанная функция в целях совместимости оставлена в Excel 2010 и в более новых версиях в специальной категории «Совместимость». В версиях же Excel 2007 и ранее она присутствует в основной группе статистических операторов.

Граница доверительного интервала определяется при помощи формулы следующего вида:

Где X – это среднее выборочное значение, которое расположено посередине выбранного диапазона.

Теперь давайте рассмотрим, как рассчитать доверительный интервал на конкретном примере. Было проведено 12 испытаний, вследствие которых были получены различные результаты, занесенные в таблицу. Это и есть наша совокупность. Стандартное отклонение равно 8. Нам нужно рассчитать доверительный интервал при уровне доверия 97%.

1. Выделяем ячейку, куда будет выводиться результат обработки данных. Щелкаем по кнопке «Вставить функцию».

Значит, чтобы посчитать уровень значимости, то есть, определить значение «Альфа» следует применить формулу такого вида:

То есть, подставив значение, получаем:

Путем нехитрых расчетов узнаем, что аргумент «Альфа» равен 0,03. Вводим данное значение в поле.

Как известно, по условию стандартное отклонение равно 8. Поэтому в поле «Стандартное отклонение» просто записываем это число.

В поле «Размер» нужно ввести количество элементов проведенных испытаний. Как мы помним, их 12. Но чтобы автоматизировать формулу и не редактировать её каждый раз при проведении нового испытания, давайте зададим данное значение не обычным числом, а при помощи оператора СЧЁТ. Итак, устанавливаем курсор в поле «Размер», а затем кликаем по треугольнику, который размещен слева от строки формул.

Группа аргументов «Значения» представляет собой ссылку на диапазон, в котором нужно рассчитать количество заполненных числовыми данными ячеек. Всего может насчитываться до 255 подобных аргументов, но в нашем случае понадобится лишь один.

Данный оператор предназначен для расчета среднего арифметического значения выбранного диапазона чисел. Он имеет следующий довольно простой синтаксис:

Аргумент «Число» может быть как отдельным числовым значением, так и ссылкой на ячейки или даже целые диапазоны, которые их содержат.

Способ 2: функция ДОВЕРИТ.СТЮДЕНТ

Кроме того, в Экселе есть ещё одна функция, которая связана с вычислением доверительного интервала – ДОВЕРИТ.СТЮДЕНТ. Она появилась, только начиная с Excel 2010. Данный оператор выполняет вычисление доверительного интервала генеральной совокупности с использованием распределения Стьюдента. Его очень удобно использовать в том случае, когда дисперсия и, соответственно, стандартное отклонение неизвестны. Синтаксис оператора такой:

Как видим, наименования операторов и в этом случае остались неизменными.

Посмотрим, как рассчитать границы доверительного интервала с неизвестным стандартным отклонением на примере всё той же совокупности, что мы рассматривали в предыдущем способе. Уровень доверия, как и в прошлый раз, возьмем 97%.

1. Выделяем ячейку, в которую будет производиться расчет. Клацаем по кнопке «Вставить функцию».

В поле «Альфа», учитывая, что уровень доверия составляет 97%, записываем число 0,03. Второй раз на принципах расчета данного параметра останавливаться не будем.

Как видим, инструменты программы Excel позволяют существенно облегчить вычисление доверительного интервала и его границ. Для этих целей используются отдельные операторы для выборок, у которых дисперсия известна и неизвестна.

Программа Эксель используется для выполнения различных статистических задач, одной из которых является вычисление доверительного интервала, который применяется как наиболее подходящая замена точечной оценки при малом объеме выборки.

Хотим сразу заметить, что сама процедура вычисления доверительного интервала довольно непростая, однако, в Excel существует ряд инструментов, призванных облегчить выполнение данной задачи. Давайте рассмотрим их.