Как посчитать критерий стьюдента в excel

Сравнение двух независимых выборок

При сравнении двух выборок проверяемая нулевая гипотеза состоит в том, что обе эти выборки происходят из нормально распределенных генеральных совокупностей с одинаковыми средними значениями:

\

Поскольку эти генеральные средние мы оцениваем при помощи выборочных средних значений, формула t-критерия приобретает вид

\

В знаменателе приведенной формулы находится стандартная ошибка разницы между выборочными средними, которая в общем виде рассчитывается как

\

где \(s_{1}^{2}\) и \(s_{2}^{2}\) — выборочные оценки дисперсии. При соблюдении условия о равенстве групповых дисперсий приведенная формула приобретает более простой вид (подробнее см. здесь). Интерпретация t-критерия, рассчитанного для двух выборок, выполняется точно так же, как и в случае с одной выборкой (см. выше).

Рассмотрим пример о суточном расходе энергии (expend) у худощавых женщин (lean) и женщин с избыточным весом (obese), приведенный в книге Питера Дальгаарда (Dalgaard P (2008) Introductory statistics with R. Springer). Данные из этого примера (подробнее см. ?energy) входят в состав пакета ISwR, сопровождающего книгу (если он у Вас не установлен, выполните команду install.packages(«ISwR»)):

library(ISwR)
data(energy)
attach(energy)
energy
   expend stature
1    9.21   obese
2    7.53    lean
3    7.48    lean
4    8.08    lean
5    8.09    lean
6   10.15    lean
7    8.40    lean
8   10.88    lean
9    6.13    lean
10   7.90    lean
11  11.51   obese
12  12.79   obese
13   7.05    lean
14  11.85   obese
15   9.97   obese
16   7.48    lean
17   8.79   obese
18   9.69   obese
19   9.68   obese

tapply(expend, stature, mean)
lean obese 
8.07 10.30

Различаются ли эти средние значения статистически? Проверим гипотезу об отсутствии разницы при помощи t-теста:

t.test(expend ~ stature)
 
        Welch Two Sample t-test
 
data:  expend by stature 
t = -3.8555, df = 15.919, p-value = 0.001411
alternative hypothesis: true difference in means is not equal to  
95 percent confidence interval:
 -3.459167 -1.004081 
sample estimates:
 mean in group lean mean in group obese 
           8.066154           10.297778

Обратите внимание на использование знака ~ в вызове функции t.test(). Это стандартный для R способ записи формул, описывающих связь между переменными

В нашем случае выражение expend ~ stature можно расшифровать как «зависимость суточного потребления энергии (expend) от статуса пациентки (stature)».

Согласно полученному значению P (p-value = 0.001411), средние значения потребления энергии у женщин из  рассматриваемых весовых групп статистически значимо различаются. Отвергая нулевую гипотезу о равенстве этих средних значений, мы рискуем ошибиться с вероятностью лишь около 0.1%. При этом истинная разница между средними значениями с вероятностью 95% находится в диапазоне от -3.5 до -1.0 (см. 95 percent confidence interval).

Следует подчеркнуть, что при выполнении двухвыборочного t-теста R по умолчанию принимает, что дисперсии сравниваемых совокупностей не равны, и, как следствие, выполняет t-тест в модификации Уэлча (подробнее см. здесь). Мы можем изменить такое поведение программы, воспользовавшись аргументом var.equal = TRUE: (от variance — дисперсия, и equal — равный):

t.test(expend ~ stature, var.equal = TRUE)
 
        Two Sample t-test
 
data:  expend by stature 
t = -3.9456, df = 20, p-value = 0.000799
alternative hypothesis: true difference in means is not equal to  
95 percent confidence interval:
 -3.411451 -1.051796 
sample estimates:
 mean in group lean mean in group obese 
           8.066154           10.297778

Р-значение стало еще меньше, и мы так же, как и после теста в модификации Уэлча, можем сделать вывод о наличии существенной разницы между средними

Однако такое совпадение выводов будет иметь место не всегда и, следовательно, на разницу между групповыми дисперсиями (или ее отсутствие) следует обращать серьезное внимание при выборе и интерпретации того или иного варианта t-теста.

Как использовать формулу ВПР для сравнения двух таблиц

Давайте узнаем, какие названия моделей отсутствуют в первом листе. Удалим из него три строки:

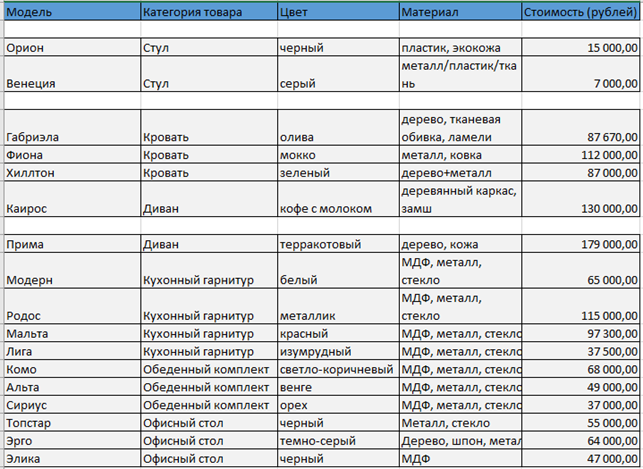
Изменения отразились в листе «Заявки» — в трех строках возникло выражение «#Н/Д». Именно эти модели мы удалили вначале.

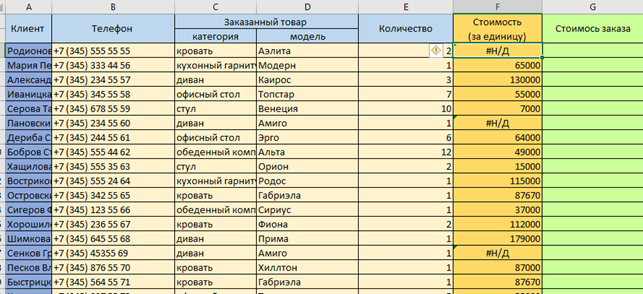
Проводить такое сравнение можно по любым другим параметрам: стоимости, цене, характеристикам товара.

Пример

Есть два прайса, менеджер хочет сравнить старые цены с новыми. Данные представлены в таком виде:

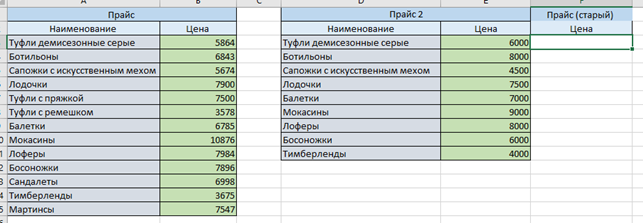
Подтянем значения из первой таблицы во вторую с помощью формулы ВПР:

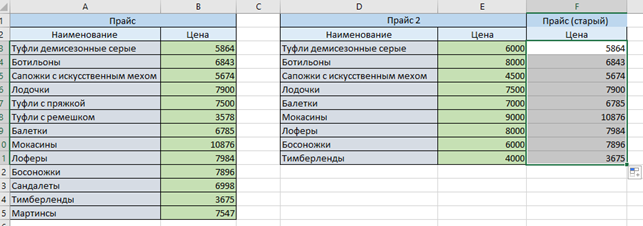
Если обновились не только цены, но и ассортимент, результат получится такой:

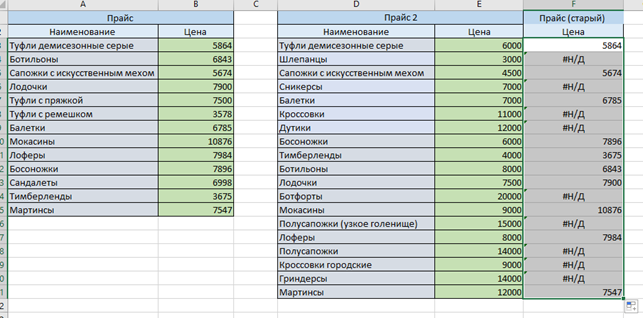
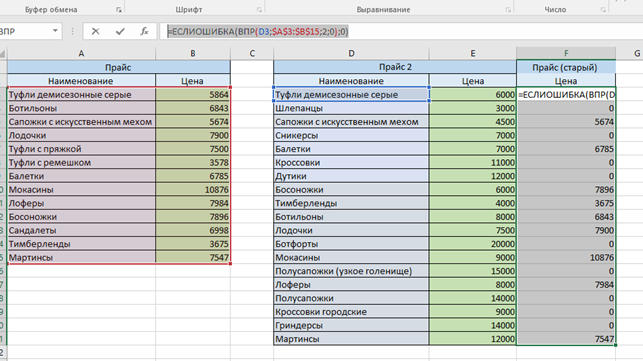
Выглядит не очень эстетично. Скорректируем с помощью функции «ЕСЛИОШИБКА». После знака «=» в строке формул введите «ЕСЛИОШИБКА(); значение, которое выводится при ошибке)». В нашем случае формула получила вид: «=ЕСЛИОШИБКА(ВПР(D3;$A$3:$B$15;2;0);0)». А таблица стала выглядеть так:

Оптимизируйте маркетинг и увеличивайте продажи вместе с Calltouch Узнать подробнее

Как пользоваться функцией распределения Стьюдента СТЮДРАСПОБР В EXCEL

Функция имеет следующий синтаксис:

• вероятность – обязательный для заполнения, принимает числовое значение вероятности для двустороннего распределения Стьюдента из диапазона от 0 (не включительно) до 1.
• степени_свободы – обязательный для заполнения, принимает числовое значение степеней свободы, которые определяют исследуемое распределение.

1. Если один из аргументов функции указан в виде значения нечислового типа данных, результатом выполнения рассматриваемой функции будет код ошибки #ЗНАЧ!. Логические значения, имена и текстовые строки, преобразуемые в числа, не приводят к возникновению ошибки. Например, функция =СТЮДРАСПОБР(“0,4”;ИСТИНА) вернет значение 1,32638.
2. Если аргумент вероятность задан числом, не находящимся в промежутке от 0 (не включительно) до 1, функция СТЮДРАСПОБР вернет код ошибки #ЧИСЛО!. Аналогичная ошибка возникает, если аргумент степени_свободы задан числом, которое меньше 1.
3. Для расчета односторонней t-величины следует в качестве аргумента вероятность указать значение удвоенной вероятности.

Выполнение F-теста и T-теста в Excel

1. Введите два набора данных в электронную таблицу. В данном случае мы рассматриваем продажу двух товаров в течение недели. Средний дневной объем продаж для каждого продукта также рассчитывается вместе со стандартным отклонением .

2. Выберите вкладку «Данные > Анализ данных».

3. Выберите F-Test To-Sample for Variance из списка, затем нажмите OK .

   F-тест очень чувствителен к аномалиям. Так что может быть безопаснее использовать тест Уэлча, но в Excel это сложнее.

4. Выберите переменный диапазон 1 и переменный диапазон 2; установить альфа (0,05 дает 95% уверенности); выберите ячейку для верхнего левого угла вывода, имея в виду, что это заполнит 3 столбца и 10 строк. Выберите ОК .

   Для диапазона переменных 1 выберите выборку с наибольшим стандартным отклонением (или дисперсией).

5. Просмотрите результаты F-теста, чтобы определить, есть ли существенная разница между дисперсиями. Результаты дают три важных значения:
   • F : отношение дисперсий.
   • P (F <= f) one-tail: Вероятность того, что переменная 1 на самом деле не имеет большей дисперсии, чем переменная 2. Если она больше, чем альфа, которая обычно равна 0,05, то между дисперсиями нет существенной разницы.
   • F Критически односторонний: значение F, необходимое для P(F <= f) = α. Если это значение больше, чем F, это также означает, что нет существенной разницы между отклонениями

   P (F <= f) также можно рассчитать, используя функцию FРАСП, используя F и степени свободы для каждого образца в качестве входных данных. Степени свободы — это просто число наблюдений в выборке минус одно.

6. Теперь, когда вы знаете, есть ли разница между дисперсиями, вы можете выбрать правильный T-критерий. Перейдите на вкладку «Данные» > «Анализ данных», затем выберите критерий Стьюдента: две выборки, предполагающие равные дисперсии, или критерий Стьюдента: две выборки, предполагающие неравные дисперсии» .

7. Какой бы вариант вы ни выбрали на предыдущем шаге, вам будет предложено ввести данные анализа в том же диалоговом окне. Для начала выберите области, содержащие шаблоны переменных области 1 и области 2 .

8. Предполагая, что вы хотите проверить отсутствие разницы между средними значениями, установите гипотетическую среднюю разницу равной нулю.
9. Установите уровень значимости на Alpha (0,05 дает достоверность 95%) и выберите ячейку в верхнем левом углу выходных данных, учитывая, что это заполнит 3 столбца и 14 строк. Выберите ОК .

10. Просмотрите результаты, чтобы определить, есть ли существенная разница между средними значениями.

Как и в F-тесте, если значение p, в данном случае P (T <= t), больше, чем альфа, существенной разницы нет. Однако в этом случае даются два значения p: одно для одностороннего теста, а другое для двустороннего теста. В этом случае используйте двустороннее значение, так как любая переменная с более высоким средним значением будет значимой разницей.

Как сделать T-тест в Excel

Прежде чем вы сможете применить T-тест, чтобы определить, есть ли статистически значимая разница между средними значениями двух образцов, вы должны сначала выполнить F-тест. Это связано с тем, что для T-теста выполняются разные вычисления в зависимости от того, есть ли существенная разница между отклонениями.

Для выполнения этого анализа вам понадобится надстройка Пакет инструментов анализа.

Проверка и загрузка надстройки Toolpak для анализа

Чтобы проверить и активировать пакет инструментов анализа, выполните следующие действия.

1. Выберите вкладку ФАЙЛ > выберите Параметры .

2. В диалоговом окне «Параметры» выберите « Надстройки» на вкладках с левой стороны.

3. В нижней части окна выберите раскрывающееся меню «Управление» , затем выберите « Надстройки Excel» . Выберите Go .

   

   

   

   

   

   

   

   

   

   

4. Убедитесь, что установлен флажок рядом с Пакетом инструментов анализа , затем выберите ОК .

5. Пакет инструментов анализа теперь активен, и вы готовы применить F-тесты и T-тесты.

Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel

С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.

Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.

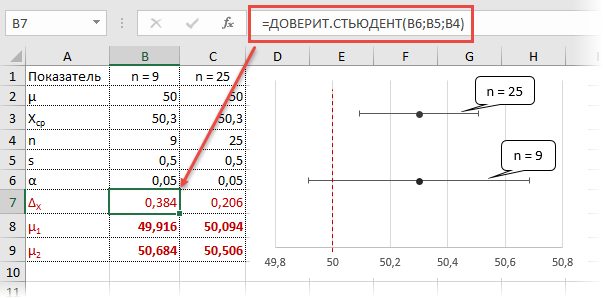
Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.

Таким образом, мы решили одну и ту же задачу тремя способами:

1. Древним подходом, сравнивая расчетное и табличное значение t-критерия2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.

Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия)

Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.

Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.

Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.

Всего доброго, будьте здоровы.

Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel

С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.

Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.

Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.

Таким образом, мы решили одну и ту же задачу тремя способами:

1. Древним подходом, сравнивая расчетное и табличное значение t-критерия2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.

Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия)

Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.

Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.

Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.

Скачать файл с примером.

Всего доброго, будьте здоровы.

Проверка гипотезы о равенстве среднего. Сложный способ

Сложный способ будет состоит из двух этапов: расчет t-критерия Стьюдента и сравнение полученного значения t-критерия с контрольным.

На первом этапе рассчитаем t-критерий Стьюдента по следующей формуле:

X₁ и X₂ — средняя длина звонков в первой и второй выборке (238,6 сек и 204,1 сек)
s₁ и s₂ — стандартные отклонения первой и второй выборок в квадрате (их дисперсии, другими словами) (201,22 и 164,72 для наших выборок)
n₁ и n₂ — число звонков в первой и второй выборках (242 и 209 звонков)

Воспользуемся листочком бумаги и калькулятором, или же посчитаем все прямо в Google Таблицах:

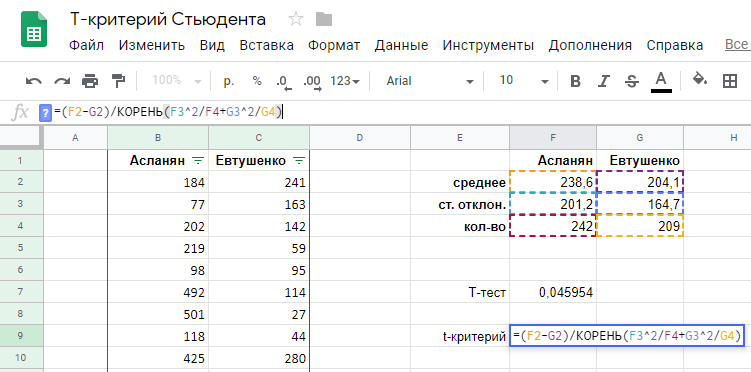
t-Критерий равен 2,0014.

Осталось разобраться, что делать с вычисленным значением нашего t-критерия.

Но перед этим посчитаем число степеней свободы по формуле n₁+n₂-2:

242 + 209 — 2 = 449 степеней свободы

Воспользуемся теперь таблицей коэффициентов Стьюдента из Википедии, найдя строку, соответствующую нашим 449 степеням свободы.

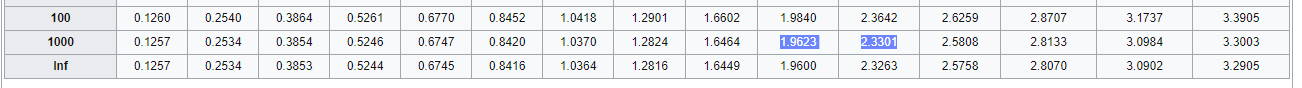
В нашем случае, строки именно для числа 449 нет, зато несложно заметить, что значения для 100 и 1000 — ближайших подходящих строк — отличаются на сотые доли, поэтому для большого числа степеней свободны подойдет любая строка.

Наше значение 2,0014 находится между 1,9623 и 2,3301: 1,9623

В шапке таблицы это соответствует 95%-му и 98%-му квантилю распределения Стьюдента, т. е. мы захватили 95%-й квантиль, но не захватили 98%-й:

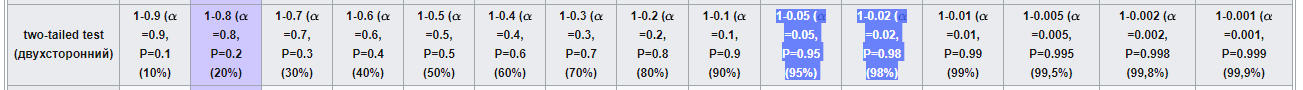
Если расчетное значение t-критерия Стьюдента больше контрольного, значит, «альтернативная гипотеза» верна с соответствующей вероятностью (95%), и выборки статистически различаются.

Если бы мы получили значение t-критерия больше, чем 2,3301 (98%), мы бы могли говорить по правильности «альтернативной гипотезы» уже с 98%-й вероятностью. Аналогично, если бы мы получили значение t-критерия меньше, чем 1,9623 (95%), но больше 1,6464 (90%), мы бы говорили о правильности гипотезы на 90%.

Вывод: расчетное значение t-критерия Стьюдента 2,0014 соответствует, по меньшей мере, 95% уверенности в том, что между выборками есть статистически значимые различия, и звонки Асланян, действительно, в среднем длиннее звонков Евтушенко.

Наша «альтернативная гипотеза» получила 95%-ое подтверждение, мы можем быть уверены в результате и принимать решение о дальнейшей работе с полученный информацией.

Каковы шаги для вычисления формулы t-теста

• 
  Шаг 1:
  
  Оцените, равны ли дисперсии генеральной совокупности. При необходимости запустите F-тест на равенство дисперсий.
• 
  Шаг 2:
  
  В зависимости от того, предполагается равенство дисперсий генеральной совокупности или нет, вы выберете правильную формулу для t-критерия.
• 
  Шаг 3:
  
  Для неравных дисперсий населения вы используете \(t = \frac{\bar X_1 — \bar X_2}{\sqrt{ \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} }}\)
• 
  Шаг 4:
  
  Для одинаковой дисперсии населения вы используете \(t = \frac{\bar X_1 — \bar X_2}{\sqrt{ \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2}(\frac{1}{n_1}+\frac{1}{n_2}) } }\)
• 
  Шаг 5:
  
  Основываясь на количестве степеней свободы и типе хвоста, вы вычисляете соответствующее p-значение, и если p-значение меньше уровня значимости, нулевая гипотеза отклоняется.

Число степеней свободы, когда предполагаются равные дисперсии генеральной совокупности, равно \(df = n_1 + n_2\), где \(n_1\) и \(n_2\) — соответствующие размеры выборки. Теперь для неравных дисперсий вычисление степеней свободы намного сложнее.

Расчет доверительного интервала с помощью t-распределения Стьюдента

С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов
. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.

Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α
, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.

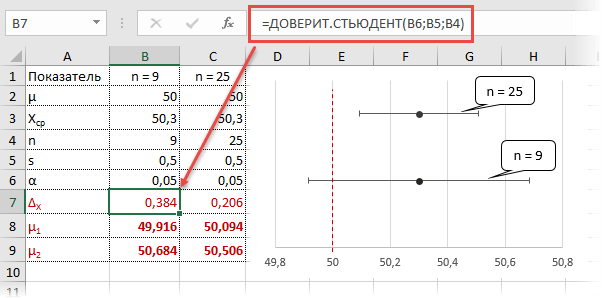
Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.

Таким образом, мы решили одну и ту же задачу тремя способами:

1. Древним подходом, сравнивая расчетное и табличное значение t-критерия 2. Более современным, рассчитав p-level, добавив степень уверенности при отклонении гипотезы. 3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.

Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия)

Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.

Напоследок предлагаю посмотреть видеоролик о том, как проводить расчеты, связанные с t-критерием Стьюдента в Excel.

Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel

С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.

Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.

Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.

Таким образом, мы решили одну и ту же задачу тремя способами:

1. Древним подходом, сравнивая расчетное и табличное значение t-критерия2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.

Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия)

Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.

Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.

Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.

Критерий Стьюдента – обобщенное название группы статистических тестов (обычно перед словом “критерий” добавляется латинская буква “t”). Чаще всего он применяется для проверки равенства средних значений в двух выборках. Давайте посмотрим, как рассчитать данный критерий в программе Excel с помощью специальной функции.

Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel

С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.

Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.

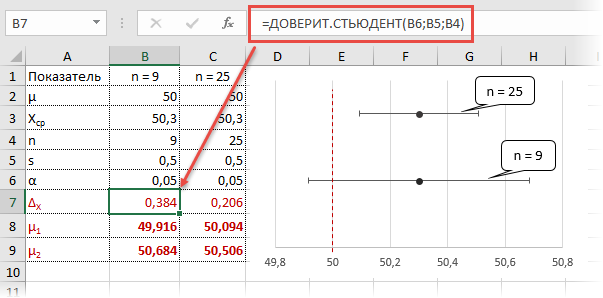
Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.

Таким образом, мы решили одну и ту же задачу тремя способами:

1. Древним подходом, сравнивая расчетное и табличное значение t-критерия2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.

Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия). Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов

Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.

Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.

Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.

Всего доброго, будьте здоровы.

Этапы статистического вывода (statistic inference)

1. Первый из них – это вопрос, который мы хотим изучить с помощью статистических методов. То есть первый этап: что изучаем? И какие у нас есть предположения относительно результата? Этот этап называется этап статистических гипотез.
2. Второй этап – нужно определиться с тем, какие у нас есть в реальности данные для того, чтобы ответить на первый вопрос. Этот этап – тип данных.
3. Третий этап состоит в том, чтобы выбрать корректный для применения в данной ситуации статистический критерий.
4. Четвертый этап это логичный этап применения интерпретации любой формулы, какие результаты мы получили.
5. Пятый этап это создание, синтез выводов относительно первого, второго, третьего, четвертого, пятого этапа, то есть что же получили и что же это в реальности значит.