Таблица производных: формулы, значение, как писать функции

Логарифмические уравнения с переменным основанием

Рассмотрим теперь уравнение, в котором есть, так называемый, логарифм с переменным основанием. То есть логарифм, у которого в основании стоит какое-то выражение, зависящее от $x$.

Пример 8

В основании логарифма стоит $(1-x)$, это переменное основание, потому что я могу подставлять различные значения $x$, и каждый раз основание логарифма будет разным. Ничего страшного в этом нет. Начинаем решать, руководствуясь тем же принципом, что и в предыдущих примерах: стараемся привести обе части уравнения к виду двух логарифмов с одинаковым основанием. Для этого нужно представить $1у$ справа в виде логарифма с основанием $(1-x)$.

Но, первым делом, выпишем ОДЗ, не забывая накладывать условия и на основание логарифма, так как оно зависит от $x$:
$$ \begin{cases}
x^2+3x+1>0, \\
1-x>0, \\
1-x\neq1.\\
\end{cases} \qquad (**)$$

Архив записей

Архив записейВыберите месяц Ноябрь 2022 (1) Сентябрь 2022 (1) Январь 2022 (2) Сентябрь 2021 (1) Июль 2021 (1) Июнь 2021 (2) Май 2021 (1) Апрель 2021 (1) Март 2021 (1) Сентябрь 2020 (1) Август 2020 (2) Июль 2020 (2) Июнь 2020 (2) Декабрь 2019 (3) Ноябрь 2019 (4) Октябрь 2019 (3) Сентябрь 2019 (2) Май 2019 (1) Октябрь 2018 (1) Июнь 2018 (1) Апрель 2018 (1) Январь 2018 (1) Ноябрь 2017 (1) Октябрь 2017 (1) Сентябрь 2017 (2) Август 2017 (4) Июль 2017 (5) Июнь 2017 (4) Май 2017 (5) Апрель 2017 (2) Март 2017 (1) Февраль 2017 (1) Январь 2017 (3) Декабрь 2016 (1) Ноябрь 2016 (2) Октябрь 2016 (3) Сентябрь 2016 (4) Август 2016 (6) Июль 2016 (9) Июнь 2016 (4) Май 2016 (5) Апрель 2016 (6) Март 2016 (5) Февраль 2016 (8) Январь 2016 (8) Декабрь 2015 (9) Ноябрь 2015 (4) Июль 2015 (1) Март 2015 (1) Февраль 2015 (1) Январь 2015 (1) Июль 2014 (1) Июль 2013 (1) Март 2013 (2) Декабрь 2012 (1) Ноябрь 2012 (1) Сентябрь 2012 (3) Август 2012 (4) Июль 2012 (4) Июнь 2012 (4) Май 2012 (4) Апрель 2012 (5) Март 2012 (7) Февраль 2012 (8) Январь 2012 (7) Декабрь 2011 (5) Ноябрь 2011 (1)

Логарифмическая производная

Если производная от логарифмов – это такая сладкая музыка, то возникает вопрос, а нельзя ли в некоторых случаях организовать логарифм искусственно? Можно! И даже нужно.

Найти производную функции

Похожие примеры мы недавно рассмотрели. Что делать? Можно последовательно применить правило дифференцирования частного, а потом правило дифференцирования произведения. Недостаток способа состоит в том, что получится огромная трехэтажная дробь, с которой совсем не хочется иметь дела.

Но в теории и практике есть такая замечательная вещь, как логарифмическая производная. Логарифмы можно организовать искусственно, «навесив» их на обе части:

Примечание: т.к. функция может принимать отрицательные значения, то, вообще говоря, нужно использовать модули: , которые исчезнут в результате дифференцирования

Однако допустимо и текущее оформление, где по умолчанию принимаются во внимание комплексные значения. Но если со всей строгостью, то и в том и в другом случае следует сделать оговорку, что

Теперь нужно максимально «развалить» логарифм правой части (формулы перед глазами?). Я распишу этот процесс очень подробно:

Собственно приступаем к дифференцированию. Заключаем под штрих обе части:

Производная правой части достаточно простая, её я комментировать не буду, поскольку если вы читаете этот текст, то должны уверенно с ней справиться.

В левой части у нас сложная функция. Предвижу вопрос: «Почему, там же одна буковка «игрек» под логарифмом?».

Дело в том, что эта «одна буковка игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ (если не очень понятно, обратитесь к статье Производная от функции, заданной неявно). Поэтому логарифм – это внешняя функция, а «игрек» – внутренняя функция. И мы используем правило дифференцирования сложной функции

В левой части как по мановению волшебной палочки у нас «нарисовалась» производная

А теперь вспоминаем, о каком таком «игреке»-функции мы рассуждали при дифференцировании? Смотрим на условие:

Окончательный ответ:

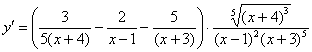
Найти производную функции

Это пример для самостоятельного решения. Образец оформления примера данного типа в конце урока.

С помощью логарифмической производной можно было решить любой из примеров № 4-7, другое дело, что там функции проще, и, может быть, использование логарифмической производной не слишком-то и оправдано.

Логарифмы со специальным обозначением

Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.

Десятичный логарифм

Десятичный логарифм обозначается lg и имеет основание 10, т.е.

Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.

Например, вычислим lg100

Натуральный логарифм

Натуральный логарифм обозначается ln и имеет основание e, то есть

Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…

Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что

И вычислить его можно таким образом:

Производная натурального логарифма — онлайн справочник для студентов

ОПРЕДЕЛЕНИЕ

Производная натурального логарифма равна единице, деленной на подлогарифмическую функцию.

Физика

166

Реклама и PR

Педагогика

Психология

Социология

Астрономия

Биология

Культурология

Экология

Право и юриспруденция

Политология

Экономика

Финансы

История

Философия

Информатика

Право

Информационные технологии

Экономическая теория

Менеджент

719

Математика

338

Химия

Микро- и макроэкономика

Медицина

Государственное и муниципальное управление

География

542

Информационная безопасность

Аудит

Безопасность жизнедеятельности

Архитектура и строительство

Банковское дело

Рынок ценных бумаг

Менеджмент организации

Маркетинг

238

Кредит

Инвестиции

Журналистика

Конфликтология

Этика

Формулы дифференцирования Производная неявной функции Частные производные Таблица производных сложных функций Таблица производных

Узнать цену работы

Узнай цену

своей работы

Имя

Принимаю Политику
конфиденциальности

Подпишись на рассылку,
чтобы не пропустить информацию об акциях

Теория к заданию 11 из ЕГЭ по математике (профиль)

Разбор сложных заданий в тг-канале:

Посмотреть

Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.

Чтобы найти наибольшее или наименьшее значение функции необходимо:

Найти производную функции $f'(х)$
Найти стационарные точки, решив уравнение $f'(х)=0$
Проверить, какие стационарные точки входят в заданный отрезок.
Вычислить значение функции на концах отрезка и в стационарных точках из п.3
Выбрать из полученных результатов наибольшее или наименьшее значение.

Чтобы найти точки максимума или минимума необходимо:

Найти производную функции $f'(х)$
Найти стационарные точки, решив уравнение $f'(х)=0$
Разложить производную функции на множители.
Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.3.
Найти точки максимума или минимума по правилу: если в точке производная меняет знак с плюса на минус, то это будет точка максимума (если с минуса на плюс, то это будет точка минимума). На практике удобно использовать изображение стрелок на промежутках: на промежутке, где производная положительна, стрелка рисуется вверх и наоборот.

Таблица производных некоторых элементарных функций:

Функция	Производная
$c$	$0$
$x$	$1$
$x^n, n∈N$	$nx^{n-1}, n∈N$
${1}/{x}$	$-{1}/{x^2}$
${1}/x{^n}, n∈N$	$-{n}/{x^{n+1}}, n∈N$
$√^n{x}, n∈N$	${1}/{n√^n{x^{n-1}}, n∈N$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	${1}/{cos^2x}$
$ctgx$	$-{1}/{sin^2x}$
$cos^2x$	$-sin2x$
$sin^2x$	$sin2x$
$e^x$	$e^x$
$a^x$	$a^xlna$
$lnx$	${1}/{x}$
$log_{a}x$	${1}/{xlna}$

Основные правила дифференцирования

1. Производная суммы и разности равна производной каждого слагаемого

$(f(x) ± g(x))′= f′(x)± g′(x)$

Пример:

Найти производную функции $f(x) = 3x^5 – cosx + {1}/{x}$

Производная суммы и разности равна производной каждого слагаемого

$f′(x)=(3x^5)′–(cosx)′+({1}/{x})’=15x^4+sinx-{1}/{x^2}$

2. Производная произведения.

$(f(x)∙g(x))′=f′(x)∙g(x)+f(x)∙g(x)′$

Пример:

Найти производную $f(x)=4x∙cosx$

$f′(x)=(4x)′∙cosx+4x∙(cosx)′=4∙cosx-4x∙sinx$

3. Производная частного

$({f(x)}/{g(x)})’={f^'(x)∙g(x)-f(x)∙g(x)’}/{g^2(x)}$

Пример:

Найти производную $f(x)={5x^5}/{e^x}$

$f'(x)={(5x^5)’∙e^x-5x^5∙(e^x)’}/{(e^x)^2}={25x^4∙e^x-5x^5∙e^x}/{(e^x)^2}$

4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

$f(g(x))′=f′(g(x))∙g′(x)$

Пример:

$f(x)= cos(5x)$

$f′(x)=cos′(5x)∙(5x)′= — sin(5x)∙5= -5sin(5x)$

Пример:

Найдите точку минимума функции $y=2x-ln⁡(x+11)+4$

Решение:

1. Найдем ОДЗ функции: $х+11>0; х>-11$

2. Найдем производную функции $y’=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$

3. Найдем стационарные точки, приравняв производную к нулю

${2x+21}/{x+11}=0$

Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю

$2x+21=0; x≠-11$

$2х=-21$

$х=-10,5$

4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.

$y'(0)={2∙0+21}/{0+11}={21}/{11}>0$

5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ — это точка минимума.

Ответ: $-10,5$

Пример:

Найдите наибольшее значение функции $y=6x^5-90x^3-5$ на отрезке $$

Решение:

1. Найдем производную функции $y′=30x^4-270x^2$

2. Приравняем производную к нулю и найдем стационарные точки

$30x^4-270x^2=0$

Вынесем общий множитель $30x^2$ за скобки

$30x^2(x^2-9)=0$

$30x^2(х-3)(х+3)=0$

Приравняем каждый множитель к нулю

$x^2=0 ; х-3=0; х+3=0$

$х=0;х=3;х=-3$

3. Выберем стационарные точки, которые принадлежат заданному отрезку $$

Нам подходят стационарные точки $х=0$ и $х=-3$

4. Вычислим значение функции на концах отрезка и в стационарных точках из п.3

$y(-5)= 6∙(-5)^5-90∙(-5)^3-5=6∙(-3125)+90∙125-5= -18750+11250-5=-7505$

$y(-3)= 6∙(-3)^5-90∙(-3)^3-5=-1458+2430-5=967$

$y(0)= -5$

$y(1)= 6∙1^5-90∙1^3-5=6-90-5= -89$

Наибольшее значение равно $967$

Ответ: $967$

Логарифмическая производная

Пример 11

Найти производную функции

Примечание

: т.к. функция может принимать отрицательные значения, то, вообще говоря, нужно использовать модули: , которые исчезнут в результате дифференцирования

Однако допустимо и текущее оформление, где по умолчанию принимаются во внимание комплексные
значения. Но если со всей строгостью, то и в том и в другом случае следует сделать оговорку, что

Собственно приступаем к дифференцированию. Заключаем под штрих обе части:

Как быть с левой частью?

В левой части у нас сложная функция
. Предвижу вопрос: «Почему, там же одна буковка «игрек» под логарифмом?».

Дело в том, что эта «одна буковка игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ
(если не очень понятно, обратитесь к статье Производная от функции, заданной неявно). Поэтому логарифм – это внешняя функция, а «игрек» – внутренняя функция. И мы используем правило дифференцирования сложной функции :

В левой части как по мановению волшебной палочки у нас «нарисовалась» производная . Далее по правилу пропорции перекидываем «игрек» из знаменателя левой части наверх правой части:

А теперь вспоминаем, о каком таком «игреке»-функции мы рассуждали при дифференцировании? Смотрим на условие:

Окончательный ответ: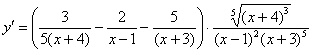

Пример 12

Найти производную функции

Это пример для самостоятельного решения. Образец оформления примера данного типа в конце урока.

Логарифмическая функция, ее свойства и график

При рассмотрении какого-либо логарифмируемого числа в качестве переменной получается логарифмическая функция, имеющая следующий вид: $y=\log _{a}x$.

Областью определения данной функции являются такие значения, которые соответствуют интервалу:

$a>0;\ a\neq 1;x>0.$

Область значений логарифмической функции определена таким образом:

$E(y) = (-\infty ;+\infty).$

На графике логарифмическая функция имеет вид кривой, которую часто называют логарифмикой. Согласно формуле, с помощью которой осуществляют замену основания логарифма, сделаем вывод о том, что:

графики логарифмических функций, имеющих разные основания, больше единицы, различаются по масштабу относительно оси y;
графики логарифмических функций для оснований, меньших, чем единица, представляют собой их зеркальное отражение по отношению к горизонтальной оси.

Изобразим графики логарифмических функций:

Согласно определению, логарифмическая функция является обратной для показательной функции $y=a^{x}$. По этой причине графические изображения данных функций будут симметричными по отношению к биссектрисе первого и третьего квадрантов. Обе эти функции трансцендентны.

Заметим следующие особенности логарифмической функции:

строгое возрастание графика, если a>1;
строгое убывание графика, если 0<a<1.

Графически изображенная логарифмическая функция в любом случае будет пересекать точку с координатами (1;0). Функция не прерывается и дифференцируется без ограничений на любом участке в рамках собственной области определений.

Ось ординат при x=0 представляет собой вертикальную асимптоту, так как:

$\lim _{x\to 0+0}\log _{a}x=-\infty$ при a>1;
$\lim _{x\to 0+0}\log _{a}x=+\infty$ при 0<a<1.

Производную логарифмической функции вычисляют по формуле:

${\frac {d}{dx}}\log _{a}x={\frac {1}{x\cdot \ln a}}$

Логарифмическая функция представляет собой непрерывное решение, которое считают единственно верным, для следующего функционального уравнения:

$f(xy)=f(x)+f(y).$

Свойства функции $y={{log}_a x\ }$, при a >1:

Областью определения данной функции является интервал $(0,+\infty )$.
Значения функции определяются, как множество действительных чисел.
Данную функцию нельзя отнести к типу четных или нечетных.
График пересекает оси координат. С осью Oy точки пересечения отсутствуют. Если $y=0$, ${{log}_a x\ }=0,\ x=1$. Функция пересекается с осью Ox в точке (1,0).
Функция является положительной, если $x\in (1,+\infty )$. Функция является отрицательной в том случае, когда $x\in (0,1)$.
$y’=\frac{1}{xlna}$.
Точки минимума и максимума: $\frac{1}{xlna}=0$, при этом корни отсутствуют, то есть максимальные и минимальные точки также отсутствуют.
Функция является возрастающей на всей области определения.
$y^{»}=-\frac{1}{x^2lna}$.
Промежутки выпуклости и вогнутости: $-\frac{1}{x^2lna}$. Функция является выпуклой на всей области, в которой определяется.
${\mathop{lim}_{x\to 0} y\ }=-\infty ,\ {\mathop{lim}_{x\to +\infty } y\ }=+\infty.$

Рассмотрим свойства функции $y={{log}_a x\ }, 0 < a < 1:$

Функция определяется на интервале $(0,+\infty).$
Значениями функции являются все числа из множества действительных.
Данную функцию нельзя отнести к типу четных или нечетных.
Отсутствуют пересечения графика с осью Oy. Если $y=0, {{log}_a x\ }=0,\ x=1$.Функция пересекает ось Ox в точке с координатами: (1,0).
Функция является положительной, если $x\in (0,1)$. Функция является отрицательной в том случае, когда $x\in (1,+\infty).$
$y’=\frac{1}{xlna}.$
Точки минимума и максимума: $ \frac{1}{xlna}=0$; в этом случае корни отсутствуют — значит, отсутствуют максимальные и минимальные точки.
Функция является убывающей на всей области, в которой она определена.
$y^{»}=-\frac{1}{x^2lna}$.
Промежутки выпуклости и вогнутости: $ -\frac{1}{x^2lna}>0$. Функция является вогнутой на всей области, в которой она определена.
$\mathop{lim}_{x\to 0} y\ =+\infty ,\ {\mathop{lim}_{x\to +\infty } y\ }=-\infty$.

Производная степенно-показательной функции

Данную функцию мы еще не рассматривали. Степенно-показательная функция – это функция, у которой и степень и основание зависят от «икс»
. Классический пример, который вам приведут в любом учебнике или на любой лекции:

Как найти производную от степенно-показательной функции?

Необходимо использовать только что рассмотренный приём – логарифмическую производную. Навешиваем логарифмы на обе части:

Как правило, в правой части из-под логарифма выносится степень:

В результате в правой части у нас получилось произведение двух функций, которое будет дифференцироваться по стандартной формуле .

Находим производную, для этого заключаем обе части под штрихи:

Дальнейшие действия несложны:

Окончательно:

Если какое-то преобразование не совсем понятно, пожалуйста, внимательно перечитайте объяснения Примера № 11.

В практических заданиях степенно-показательная функция всегда будет сложнее, чем рассмотренный лекционный пример.

Пример 13

Найти производную функции

Используем логарифмическую производную.

В правой части у нас константа и произведение двух множителей – «икса» и «логарифма логарифма икс» (под логарифм вложен еще один логарифм). При дифференцировании константу, как мы помним, лучше сразу вынести за знак производной, чтобы она не мешалась под ногами; и, конечно, применяем знакомое правило :

Вам кажется, что до экзамена еще много времени? Это месяц? Два? Год? Практика показывает, что ученик лучше всего справляется с экзаменом в том случае, если начал готовиться к нему заблаговременно. В ЕГЭ немало сложных заданий, который стоят на пути школьника и будущего абитуриента к высшим баллам. Эти преграды нужно научиться преодолевать, к тому же, делать это несложно. Вам необходимо понять принцип работы с различными заданиями из билетов. Тогда и с новыми не возникнет проблем.

Логарифмы на первый взгляд кажутся невероятно сложными, но при детальном разборе ситуация значительно упрощается. Если вы хотите сдать ЕГЭ на высший балл, вам стоит разобраться в рассматриваемом понятии, что мы и предлагаем сделать в этой статье.

Для начала разделим эти определения. Что такое логарифм (log)? Это показатель степени, в которую надо возвести основание, чтобы получить указанное число. Если непонятно, разберем элементарный пример.

В этом случае основание, стоящее внизу, необходимо возвести во вторую степень, чтобы получить число 4.

Теперь разберемся со вторым понятием. Производная функции в любом виде называется понятие, характеризующее изменение функции в приведенной точке. Впрочем, это школьная программа, и если вы испытываете проблемы с данными понятиями по отдельности, стоит повторить тему.

Производная логарифма

В задания ЕГЭ по этой теме можно привести несколько задач в качестве примера. Для начала самая простая логарифмическая производная. Необходимо найти производную следующей функции.

Нам нужно найти следующую производную

Существует специальная формула.

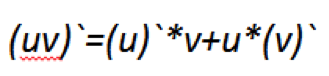
В этом случае x=u, log3x=v. Подставляем значения из нашей функции в формулу.

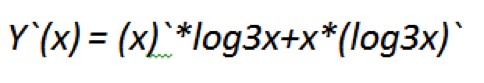
Производная x будет равняться единице. С логарифмом немного труднее. Но принцип вы поймете, если просто подставите значения. Напомним, что производной lg x называется производная десятичного логарифма, а производная ln х — это производная от натурального логорифма (по основанию e).

Теперь просто подставьте полученные значения в формулу. Попробуйте сами, далее сверим ответ.

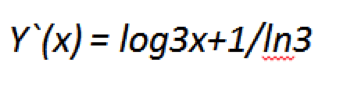
В чем здесь может быть проблема для некоторых? Мы ввели понятие натурального логарифма. Расскажем о нем, а заодно разберемся, как решать задачи с ним. Ничего сложного вы не увидите, особенно, когда поймете принцип его работы. К нему вам стоит привыкнуть, так как он нередко используется в математике (в высших учебных заведениях тем более).

Примеры вычисления производной логарифма

Пример

Задание. Вычислить производную функции $y(x)=log _{3} x$

Решение. Согласно формуле имеем, что

$$y^{prime}(x)=left(log _{3} xright)^{prime}=frac{1}{x ln 3}$$

Ответ. $y^{prime}(x)=frac{1}{x ln 3}$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти производную функции $y(x)=2 lg x$

Решение. Искомая производная равна:

$$y^{prime}(x)=(2 lg x)^{prime}$$

По правилам дифференцирования выносим константу за знак производной, а логарифм в условии десятичный, значит его основание равно 10, тогда имеем:

$$y^{prime}(x)=2 cdot(lg x)^{prime}=2 cdot frac{1}{x ln 10}=frac{2}{x ln 10}$$

Ответ. $y^{prime}(x)=frac{2}{x ln 10}$

Примечания

Алгебра и начала анализа. Учебник для 10-11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 233.
, с. 187.
, с. 34.
, с. 189..
↑
, Том I, стр. 159-160.
, Том I, стр. 164.
Рудио Ф. О квадратуре круга (Архимед, Гюйгенс, Ламберт, Лежандр). — Изд. 3-е. — М.-Л.: ОГИЗ, 1936. — С. 89. — 237 с. — (Классики естествознания).
Flashman, Martin. . Дата обращения 30 июня 2011.
J J O’Connor and E F Robertson. . The MacTutor History of Mathematics archive (сентябрь 2001). Дата обращения 30 июня 2011.
↑ , с. 325-328..
Рыбников К. А. История математики. В двух томах. — М.: Изд. МГУ, 1963. — Т. II. — С. 27, 230—231..
↑ , с. 623..
, с. 45-46, 99-100..
Дербишир, Джон. Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. — Астрель, 2010. — 464 с. — ISBN 978-5-271-25422-2.
Weisstein, Eric W. (англ.). MathWorld. Дата обращения 26 апреля 2012.
Иванов М. Г. Размер и размерность // «Потенциал», август 2006.
Головин С. Ю. . Дата обращения 17 апреля 2012.
. Дата обращения 17 апреля 2012.
Welford, A. T. Fundamentals of skill. — London: Methuen, 1968. — P. 61. — ISBN 978-0-416-03000-6.

Производная степенно-показательной функции

Как найти производную от степенно-показательной функции?

Как правило, в правой части из-под логарифма выносится степень:

Находим производную, для этого заключаем обе части под штрихи:

Дальнейшие действия несложны:

Окончательно:

Если какое-то преобразование не совсем понятно, пожалуйста, внимательно перечитайте объяснения Примера № 11.

Пример 13

Найти производную функции

Используем логарифмическую производную.

Происхождение термина

Сначала может показаться, что поскольку наша система счисления имеет основание 10, то это основание является более «натуральным», чем основание e. Но математически число 10 не является особо значимым. Его использование скорее связано с культурой, оно является общим для многих систем счисления, и связано это, вероятно, с числом пальцев у людей. Некоторые культуры основывали свои системы счисления на других основаниях: 5, 8, 12, 20 и 60.

log_e является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:

(loga⁡x)′=(1ln⁡a⋅ln⁡x)′=1ln⁡a(ln⁡x)′=1xln⁡a{\displaystyle (\log _{a}x)’=\left({\frac {1}{\ln a}}\cdot \ln {x}\right)’={\frac {1}{\ln a}}(\ln {x})’={\frac {1}{x\ln a}}}

Если основание a{\displaystyle a} равно e{\displaystyle e}, то производная равна просто 1x{\displaystyle {\frac {1}{x}}}, а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора, чего нельзя сказать о других логарифмах.

Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николас Меркатор называли их логарифмус натуралис за несколько десятилетий до того, как Ньютон и Лейбниц разработали дифференциальное и интегральное исчисление.

Вывод формул производных натурального логарифма и логарифма по основанию a

Производная натурального логарифма от x равна единице, деленной на x:(1)
(ln
x)′ =

Производная логарифма по основанию a равна единице, деленной на переменную x, умноженную на натуральный логарифм от a
:
(2)
(log
a x)′ =

Доказательство

Пусть есть некоторое положительное число, не равное единице. Рассмотрим функцию, зависящую от переменной x
,
которая является логарифмом по основанию :
.
Эта функция определена при .
Найдем ее производную по переменной x
.
По определению, производная является следующим пределом:(3)
.

Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам нужно знать следующие факты:А)
Свойства логарифма . Нам понадобятся следующие формулы:(4)
;
(5)
;
(6)
;
Б)
Непрерывность логарифма и свойство пределов для непрерывной функции:(7)
.
Здесь — некоторая функция, у которой существует предел и этот предел положителен.В)
Значение второго замечательного предела:(8)
.