Как найти высоту трапеции по уравнению

Формула для нахождения высоты трапеции

Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие не параллельны. Она имеет множество свойств и характеристик, одной из которых является ее высота.

Высота трапеции — это отрезок, проведенный перпендикулярно основанию и соединяющий два параллельных основания. Найти высоту трапеции можно с использованием специальной формулы.

Формула для нахождения высоты трапеции зависит от известных данных, которыми являются длины оснований и длина боковой стороны. Если известны основания a и b, а также боковая сторона c, то формула для вычисления высоты будет следующей:

• если основание a больше основания b, то высота трапеции вычисляется по формуле: h = 2c / (a + b)
• если основание b больше основания a, то высота трапеции вычисляется по формуле: h = 2c / (b + a)

Из этих формул видно, что высота трапеции обратно пропорциональна сумме длин оснований и прямо пропорциональна длине боковой стороны. Зная значения оснований и боковой стороны, можно легко вычислить высоту трапеции по соответствующим формулам.

Использование длины оснований и площади

Одним из способов найти высоту трапеции является использование длины оснований и площади. Для этого необходимо знать значения длины оснований и площади трапеции.

Как найти высоту трапеции с помощью длины оснований и площади? Для начала, найдите площадь трапеции по формуле: S = ((a + b) * h) / 2, где a и b — длины оснований, h — высота. Затем, зная площадь трапеции и одну из длин оснований, можно найти высоту по формуле: h = (2 * S) / (a + b).

Пример: допустим, у нас есть трапеция с длиной одного основания a = 5 см, длиной второго основания b = 3 см и площадью S = 10 см². Чтобы найти высоту, воспользуемся формулой h = (2 * 10) / (5 + 3) = 2,5 см.

Таким образом, используя длины оснований и площадь трапеции, можно легко найти ее высоту. Этот метод особенно полезен, когда известны значения длин оснований и площади, а высоту нужно найти.

Применение длины боковой стороны и углов

Как найти высоту трапеции? Для этого можно использовать длину боковой стороны и углы, которые заданы. Если известны длины боковых сторон ихальцев, то высота может быть рассчитана с помощью тригонометрических функций.

Чтобы найти высоту, возьмем одну из боковых сторон и разделим ее на синус угла, образованного этой стороной и основанием трапеции. Полученное значение будет являться высотой трапеции.

Также возможно рассчитать высоту трапеции, используя теорему Пифагора и известную длину оснований и боковых сторон. Находим разность квадратов длин оснований и боковых сторон, затем находим квадратный корень от полученного значения. Это и будет высота трапеции.

Если известны только углы трапеции, то высоту можно рассчитать, используя теорему синусов. Найдем синус угла, образованного этой стороной и основанием трапеции, затем поделим длину боковой стороны на найденный синус. Полученное значение будет являться высотой трапеции.

Площадь криволинейной трапеции

Отдельный случай – это криволинейная трапеция
. Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.

Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:

Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь Ответ:
площадь заданной криволинейной трапеции равняется 4.

Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.

Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы. Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы — непродуктивно. В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции

Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы

Основные определения и свойства трапеций

Тип претензии	Фигура	Рисунок	Формулировка
Определение	Трапеция		Трапеция – это квадрат, у которого две стороны параллельны, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а непараллельные стороны называются сторонами трапеции
Определение	Диагонали трапеция		Диагонали трапеции – это отрезки, соединяющие противоположные углы трапеции
Определение	Высота трапеция		Высотой трапеции называется перпендикуляр, опущенный из любой точки основания трапеции на другое основание или его продолжение
Свойство	Пересечение диагоналей		Точка пересечения диагоналей трапеции, точка пересечения продолжений сторон и середины оснований лежат на прямой Узнать больше об этом объекте
Определение	Центральная линия трапеция		Средняя линия трапеции – это отрезок, соединяющий середины сторон трапеции
Свойство	Средняя линия трапеции параллельна основаниям трапеции и равна половине их суммы Посмотреть доказательства
Свойство	Половина секторов углов на стороне трапеции		Биссектрисы углов на стороне трапеции перпендикулярны

Определение: трапеция
	Трапеция – это квадрат, у которого две стороны параллельны, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а непараллельные стороны называются сторонами трапеции
Определение: диагонали трапеции
	Диагонали трапеции – это отрезки, соединяющие противоположные углы трапеции
Определение: высота трапеции
	Высотой трапеции называется перпендикуляр, опущенный из любой точки основания трапеции на другое основание или его продолжение
Свойство: пересечение диагоналей
	Точка пересечения диагоналей трапеции, точка пересечения продолжений сторон и середины оснований лежат на прямой Узнать больше об этом объекте
Определение: центральная линия трапеции
	Средняя линия трапеции – это отрезок, соединяющий середины сторон трапеции
Свойство: центральная линия трапеции
	Средняя линия трапеции параллельна основаниям трапеции и равна половине их суммы Посмотреть доказательства
Свойство: биссектрисы углов на стороне трапеции
	Биссектрисы углов на стороне трапеции перпендикулярны

Трапеция

Определение: Трапеция – это квадрат, у которого две стороны параллельны, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а непараллельные стороны называются сторонами трапеции

Диагонали трапеции

Определение: Диагонали трапеции – это отрезки, соединяющие противоположные углы трапеции

Трапециевидная высота

Определение: Высотой трапеции называется перпендикуляр, опущенный из любой точки основания трапеции на другое основание или его продолжение

Пересечение диагоналей

Свойство: Пересечение диагоналей трапеции, пересечение продолжений сторон и середин оснований лежат на прямой Узнать больше об этом объекте

Средняя линия трапеции

Определение: Средняя линия трапеции – это отрезок, соединяющий середины сторон трапеции Свойство: Средняя линия трапеции параллельна основаниям трапеции и равна половине их суммы Посмотреть доказательства

Половина секторов углов на стороне трапеции

Свойство: Биссектрисы углов, лежащих на стороне трапеции, перпендикулярны

Подробнее о свойствах срединной линии трапеции можно прочитать в разделе нашего справочника «Средняя линия трапеции».

В разделе нашего справочника «Виды четырехугольников» представлена ​​схема классификации трапеций. В этом же разделе представлена ​​таблица, описывающая разные виды трапеций.

Площадь криволинейной трапеции

Отдельный случай – это криволинейная трапеция
. Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.

Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:

Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь Ответ:
площадь заданной криволинейной трапеции равняется 4.

Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.

Как найти высоту равнобедренной трапеции?

Равнобедренной трапецией, называют трапецию, у которой длины боковых сторон равны между собой. Прямая, проведенная через середины оснований такой трапеции будет осью симметрии. Частным случаем является трапеция, диагонали которой перпендикулярны друг другу, тогда высота h, будет равна полусумме оснований.

Рассмотрим случай, если диагонали не перпендикулярны друг другу. В равнобочной (равнобедренной) трапеции равны углы при основаниях и длины диагоналей равны. Также известно, что все вершины равнобокой трапеции касаются линии окружности, проведенной вокруг этой трапеции.

Рассмотрим рисунок. ABCD- равнобедренная трапеция. Известно, что основания трапеции параллельны, значит, BC = b параллельно AD = a, сторона AB = CD = c, значит, углы при основаниях соответственно равны, можно записать угол BAQ = CDS = α, и угол ABC = BCD = β. Таким образом, делаем вывод о равенстве треугольника ABQ треугольнику SCD, значит, отрезок

AQ = SD = (AD — BC)/2 = (a — b)/2.

Имея по условию задачи величины оснований a и b, и длину боковой стороны с, найдем высоту трапеции h, равную отрезку BQ.

Рассмотрим прямоугольный треугольник ABQ. ВО — высота трапеции, перпендикулярна основанию AD, значит и отрезку AQ. Сторону AQ треугольника ABQ, найдем, воспользовавшись выведенной нами ранее формулой:

Имея значения двух катетов прямоугольного треугольника, найдем гипотенузу BQ= h. Используем теорему Пифагора.

AB²= AQ² + BQ²

Подставим данные задачи:

c² = AQ² + h².

Получим формулу для нахождения высоты равнобедренной трапеции:

h = √(c²-AQ²).

Пример

Дана равнобедренная трапеция ABCD, где основание AD = a = 10см, основание BC = b = 4см, а боковая сторона AB = c = 12см. При таких условиях, рассмотрим на примере, как найти трапеции высоту, равнобедренной трапеции АВСД.

Найдем сторону AQ треугольника ABQ, подставив известные данные:

AQ = (a — b)/2 = (10-4)/2=3см.

Теперь подставим значения сторон треугольника в формулу теоремы Пифагора.

h = √(c²- AQ²) = √(12²- 3²) = √135 = 11.6см.

Ответ. Высота h равнобедренной трапеции ABCD составляет 11.6 см.

Геометрия – одна из наук, с применением которой на практике человек сталкивается практически ежедневно. Среди многообразия геометрических фигур отдельного внимания заслуживает и трапеция. Она представляет собой выпуклую фигуру с четырьмя сторонами, из которых две параллельны между собой. Последние называются основаниями, а оставшиеся две – боковыми сторонами. Отрезок, перпендикулярный основаниям и определяющий величину промежутка между ними, и будет высотой трапеции. Каким же образом можно вычислить его длину?

Онлайн калькулятор

Через длины оснований и высоту

Чему равна площадь трапеции, если: основание a = основание b = высота h = Ответ: S = ед.²Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Чему равна площадь трапеции если известны основания a и b, а также высота h?

S = ½ ⋅ (a + b) ⋅ h

Пример

Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:

S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²

Через среднюю линию и высоту

Чему равна площадь трапеции, если: средняя линия m = высота h = Ответ: S = ед.²Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Чему равна площадь трапеции если известны средняя линия m и высота h?

S = m ⋅ h

Пример

Если у трапеции средняя линия m = 6 см, а высота h = 4 см, то её площадь:

S = 6 ⋅ 4 = 24 см²

Через длины сторон и оснований

Чему равна площадь трапеции, если: основание a = основание b = сторона c = сторона d = Ответ: S = ед.²Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Чему равна площадь трапеции если известны основания a и b, а также стороны c и d?

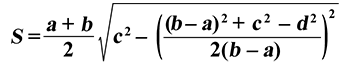
Пример

Если у трапеции основание a = 2 см, основание b = 6 см, сторона c = 4 см, а сторона d = 7 см, то её площадь:

S ≈ 13.555 см²

Через диагонали и угол между ними

Чему равна площадь трапеции, если: диагональ d₁ = диагональ d₂ = угол α = Ответ: S = ед.²Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Чему равна площадь трапеции если известны диагонали d₁ и d₂ и угол между ними α?

S = ½ ⋅ d₁ ⋅ d₂ ⋅ sin(α)

Пример

Если у трапеции одна диагональ d₁ = 5 см, другая диагональ d₂ = 7 см, а угол между ними ∠α = 30°, то её площадь:

S = ½ ⋅ 5 ⋅ 7 ⋅ sin (30) = 17.5 ⋅ 0.5= 8.75 см²

Площадь равнобедренной трапеции

Через среднюю линию, боковую сторону и угол при основании

Чему равна площадь трапеции, если: средняя линия m = сторона c = угол α = Ответ: S = ед.²Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?

S = m ⋅ c ⋅ sin(α)

Пример

Если у равнобедренной трапеции средняя линия m = 6 см, сторона c = 4 см, а угол при основании ∠α = 30°, то её площадь:

S = 6 ⋅ 4 ⋅ sin (30) = 24 ⋅ 0.5 = 12 см²

Через радиус вписанной окружности

Чему равна площадь трапеции, если: радиус r = угол α = Ответ: S = ед.²Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Чему равна площадь равнобедренной трапеции если радиус вписанной окружности r, a угол при основании α?

Пример

Если у равнобедренной трапеции радиус вписанной окружности r = 5 см, а угол при основании ∠α = 30°, то её площадь:

S = 4 ⋅ 5² / sin (30) = 100 / 0.5 = 200 см²

Основные свойства трапеции

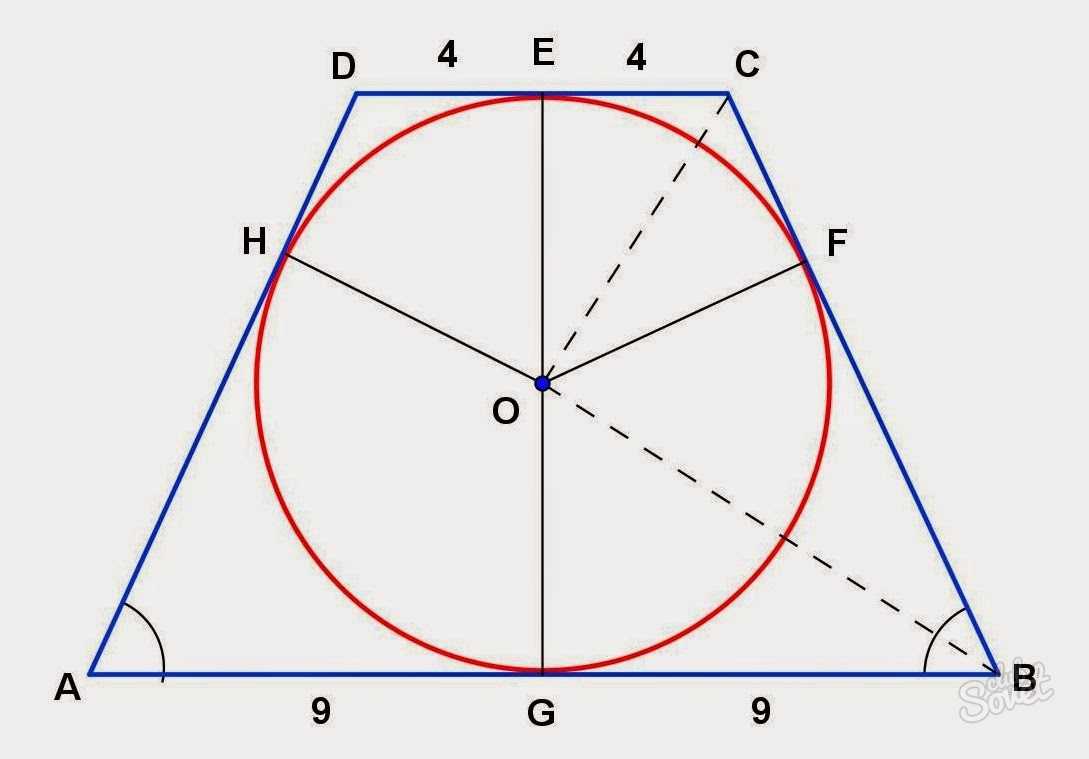
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин сторон:

Средняя линия трапеции делит пополам любой отрезок, соединяющий основания, а также диагонали:

Средняя линия трапеции параллельна основаниям и равна половине их суммы:

Точка пересечения диагоналей трапеции с серединами оснований лежит на прямой.

В трапеции сторона видна из центра вписанной окружности под углом 90°.

Каждая диагональ в точке пересечения делится на две части с таким отношением длин, как отношение между основаниями:

Диагонали трапеций d1 и d2 связаны со сторонами соотношением:

Свойства подобия

Продолжая развивать эту тему, можно доказывать и другие интересные особенности трапеций. Так, с помощью подобия можно доказать свойство отрезка, который проходит через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям. Для этого решим следующую задачу: необходимо найти длину отрезка РК, который проходит через точку О. Из подобия треугольников АОД и БОС следует, что АО/ОС=АД/БС. Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО=БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК=БС*АД/(БС+АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.

Рассмотрим следующее качество трапеции, которое называют свойством четырех точек. Точки пересечения диагоналей (О), пересечения продолжения боковых сторон (Е), а также середины оснований (Т и Ж) всегда лежат на одной линии. Это легко доказывается методом подобия. Полученные треугольники БЕС и АЕД подобны, и в каждом из них медианы ЕТ и ЕЖ делят угол при вершине Е на равные части. Следовательно, точки Е, Т и Ж лежат на одной прямой. Точно так же на одной прямой располагаются точки Т, О, и Ж. Все это следует из подобия треугольников БОС и АОД. Отсюда делаем вывод, что все четыре точки — Е, Т, О и Ж — будут лежать на одной прямой.

Используя подобные трапеции, можно предложить учащимся найти длину отрезка (ЛФ), который разбивает фигуру на две подобные. Данный отрезок должен быть параллелен основаниям. Так как полученные трапеции АЛФД и ЛБСФ подобны, то БС/ЛФ=ЛФ/АД. Отсюда следует, что ЛФ=√(БС*АД). Получаем, что отрезок, разбивающий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.

Рассмотрим следующее свойство подобия. В его основе лежит отрезок, который делит трапецию на две равновеликие фигуры. Принимаем, что трапеция АБСД разделена отрезком ЕН на две подобные. Из вершины Б опущена высота, которая разбивается отрезком ЕН на две части — В1 и В2. Получаем: ПАБСД/2 = (БС+ЕН)*В1/2 = (АД+ЕН)*В2/2 и ПАБСД = (БС+АД)*(В1+В2)/2. Далее составляем систему, первое уравнение которой (БС+ЕН)*В1 = (АД+ЕН)*В2 и второе (БС+ЕН)*В1 = (БС+АД)*(В1+В2)/2. Отсюда следует, что В2/ В1 = (БС+ЕН)/(АД+ЕН) и БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Получаем, что длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований: √((БС2+АД2)/2).

Площадь каких видов трапеций может рассчитать наш калькулятор?

Калькулятор площади трапеции может рассчитать площадь всех видов трапеций, включая прямоугольную, равнобокую, равнобедренную, криволинейную и изогнутую трапеции. Для расчета площади трапеции необходимо знать длины ее оснований и высоту. Если речь идет о криволинейной трапеции или изогнутой трапеции, то также необходимо знать длины наклонных боковых сторон.

Калькулятор площади трапеции учитывает все эти параметры и автоматически рассчитывает площадь трапеции, когда вы вводите соответствующие значения в поля веб-интерфейса калькулятора.

Вопросы и ответы

При расчете площади трапеции могут возникать различные вопросы. Вот некоторые из наиболее частых вопросов и ответы на них:

Как найти высоту трапеции, если она неизвестна?

Высота трапеции является перпендикулярной линией, проведенной от одного основания до другого. Если вы не знаете высоту, но знаете длины оснований и площадь трапеции, то можно использовать формулу S = (a + b)h/2, где S — площадь, a и b — длины оснований, h — высота. Решая эту формулу относительно h, вы получите высоту трапеции: h = 2S / (a + b).

Как рассчитать площадь криволинейной трапеции?

Чтобы рассчитать площадь криволинейной трапеции, необходимо знать длины ее оснований и наклонных боковых сторон, а также высоту. Затем вы можете использовать формулу для площади трапеции: S = (a + b)h/2, где a и b — длины оснований, h — высота. Для криволинейной трапеции вместо a и b необходимо использовать длины соответствующих наклонных сторон.

Как проверить, что я правильно рассчитал площадь трапеции?

Вы можете проверить правильность своих расчетов, используя формулу для площади трапеции. Также вы можете использовать наш онлайн калькулятор площади трапеции, чтобы проверить свои расчеты. Если вы измерили длины сторон и углы трапеции с помощью инструментов, то также можете проверить свои измерения, сравнив их с теоретическими значениями.

Можно ли рассчитать площадь трапеции, зная только диагонали?

Если вы знаете длины диагоналей трапеции и угол между ними, то можно использовать формулу для расчета площади трапеции: S = (1/2)d1d2sin(theta), где d1 и d2 — диагонали, а theta — угол между ними.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

• Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
• Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
• Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
• Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
• Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
• Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
• Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
• Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
• Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
• Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.

Как вычислить наибольшую высоту треугольника

Как найти наибольшую или наименьшую высоту треугольника? Чем меньше высота треугольника, тем больше проведенная к ней высота. То есть наибольшая из высот треугольника — та, которая проведена к его наименьшей стороне. Наименьшая высота — та, которая проведена к наибольшей из сторон треугольника.

Чтобы найти наибольшую высоту треугольника, можно площадь треугольника разделить на длину стороны, к которой проведена эта высота (то есть на длину наименьшей из сторон треугольника).

Соответственно, для нахождения наименьшей высоты треугольника можно площадь треугольника разделить на длину его наибольшей стороны.

Найти наименьшую высоту треугольника, стороны которого равны 7 см, 8 см и 9 см.

AC=7 см, AB=8 см, BC=9 см.

Найти: наименьшую высоту треугольника.

Наименьшая из высот треугольника — та, которая проведена к его наибольшей стороне. Значит, нужно найти высоту AF, проведенную к стороне BC.

Для удобства записи введем обозначения

BC=a, AC=b, AB=c, AF=ha.

Высота треугольника равна частному от деления удвоенной площади треугольника на сторону, к которой эта высота проведена. Площадь треугольника по сторонам можно найти с помощью формулы Герона. Поэтому

Найти наибольшую сторону треугольника со сторонами 1 см, 25 см и 30 см.

AC=25 см, AB=11 см, BC=30 см.

наибольшую высоту треугольника ABC.

Наибольшая высота треугольника проведена к его наименьшей стороне.

Значит, нужно найти высоту CD, проведенную к стороне AB.

Формулы для нахождения высоты треугольника

В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.

Нахождение высоты треугольника

Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.

Высота в разностороннем треугольнике

Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

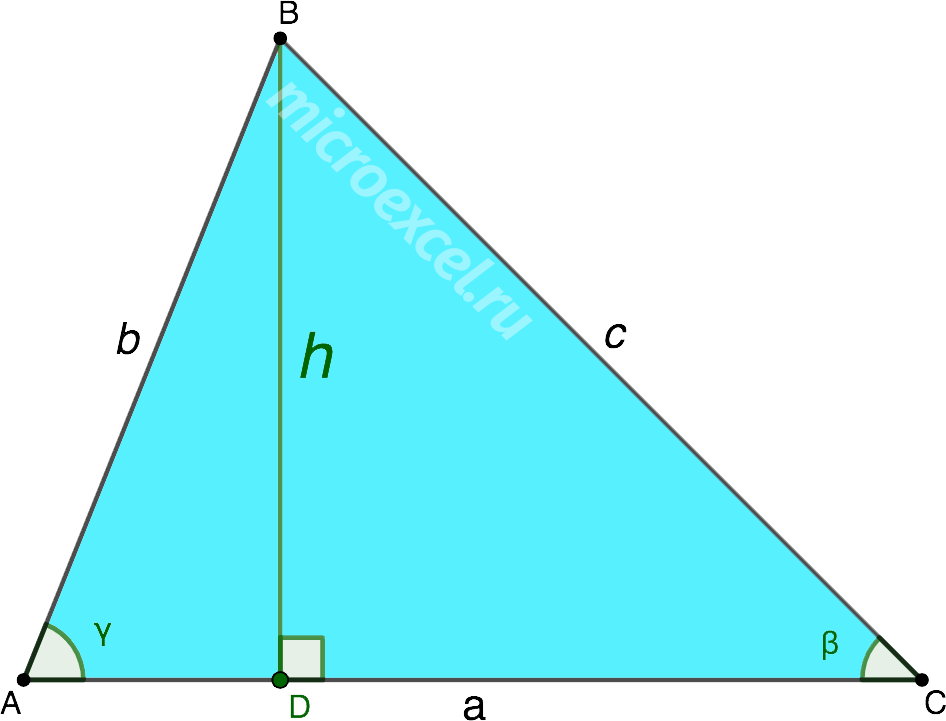
1. Через площадь и длину стороны

где S – площадь треугольника.

2. Через длины всех сторон

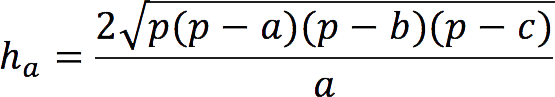
где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности

где R – радиус описанной окружности.

Длина высоты h_a, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:

Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:

1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.

Высота в равностороннем треугольнике

Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:

Примеры задач

Задача 1 Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.

Решение В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2 Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.

Решение Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

https://amdy.su/wp-admin/options-general.php?page=ad-inserter.php#tab-8

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

Виды трапеций

В зависимости от того, какие стороны имеет фигура, какие углы образованы при основаниях, выделяют три вида четырехугольника: прямоугольная, разнобокая и равнобокая.

Разнобокая

Существует две формы: остроугольная и тупоугольная
. ABCD остроугольна только в том случае, когда углы при основании (AD) острые, а длины сторон разные. Если величина одного угла число Пи/2 более (градусная мера более 90°), то получим тупоугольную.

Если боковины по длине равны

Рисунок 3. Вид равнобокой трапеции

Если непараллельные стороны равны по длине, тогда ABCD называется равнобокой (правильной). При этом у такого четырехугольника градусная мера углов при основании одинакова, их угол будет всегда меньше прямого. Именно по этой причине равнобедренная никогда не делится на остроугольные и тупоугольные. Четырехугольник такой формы имеет свои специфические отличия, к числу которых относят:

1. Отрезки соединяющие противоположные вершины равны.
2. Острые углы при большем основании составляют 45° (наглядный пример на рисунке 3).
3. Если сложить градусные меры противоположных углов, то в сумме они будут давать 180°.
4. Вокруг любой правильной трапеции можно построить .
5. Если сложить градусную меру противоположных углов, то она равна π.

Более того, в силу своего геометрического расположения точек существуют основные свойства равнобедренной трапеции
:

Значение угла при основании 90°

Перпендикулярность боковой стороны основания — емкая характеристика понятия «прямоугольная трапеция». Двух боковых сторон с углами при основании быть не может,
потому как в противном случае это будет уже прямоугольник. В четырехугольниках такого типа вторая боковая сторона всегда будет образовывать острый угол с большим основанием, а с меньшим — тупой. При этом, перпендикулярная сторона также будет являться и высотой.

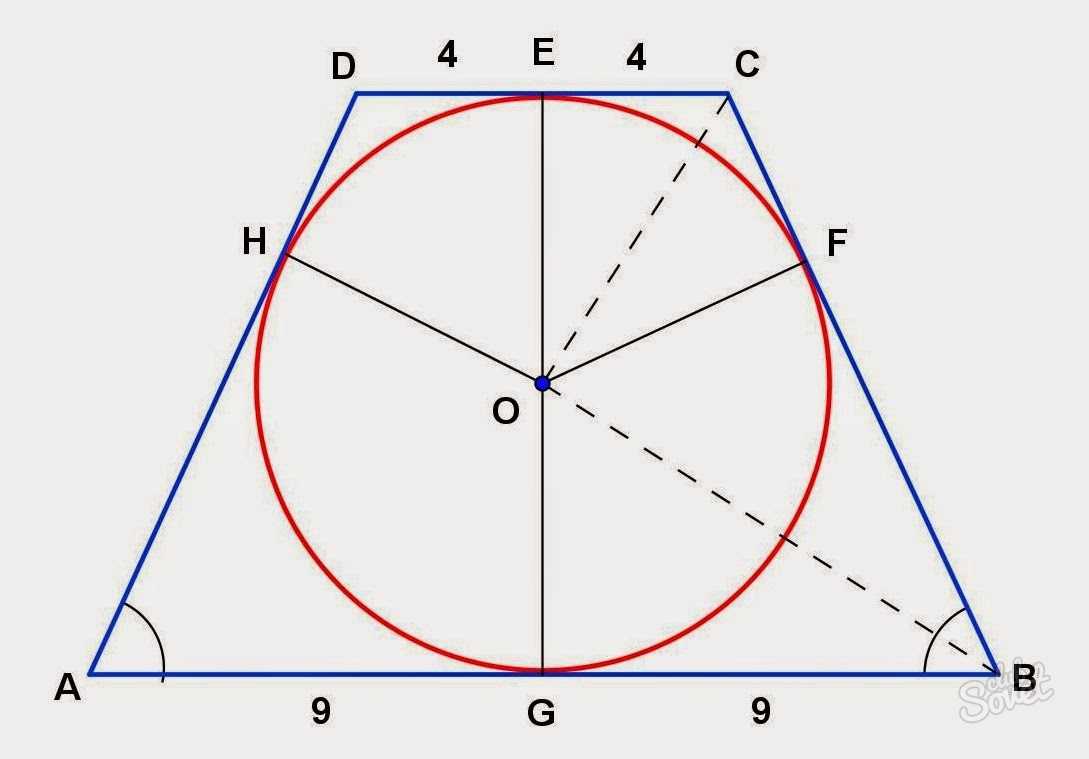
Найти высоту равнобедренной трапеции

Итак, если с = d, то h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 = √c 2 -(a-b) 2 /4,
a, b – стороны-основания четырехугольника,
c = d – его боковые стороны.

При наличии величины углов, образованных двумя сторонами (основанием и боковой), высоту трапеции определяет следующее соотношение:

h = c* sinα,
h = с * tgα *cosα = с * tgα * (b – a)/2c = tgα * (b-a)/2,

α – угол в основании фигуры,
a, b (a
c = d – его боковые стороны.

Если даны величины диагоналей фигуры, то выражение для нахождения высоты фигуры видоизменится, т.к. d1 = d2:

h = d1 2 /(a+b)*sinγ = d1 2 /(a+b)*sinφ,

h = d1 2 /2*l*sinγ = d1 2 /2*l*sinφ.

С такой формой как трапеция, мы встречаемся в жизни довольно часто. К примеру, любой мост который выполнен из бетонных блоков, является ярким примером. Более наглядным вариантом можно считать рулевое управление каждого транспортного средства и прочее. О свойствах фигуры было известно еще в Древней Греции
, которую более детально описал Аристотель в своем научном труде «Начала». И знания, выведенные тысячи лет назад актуальны и по сегодня. Поэтому ознакомимся с ними более детально.

Заключение

Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.

Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Добрый день, дорогие друзья! Сегодня у нас тема — трапеция решение задач по геометрии.
Прежде чем начинать разбирать задачи, давайте вспомним, что такое трапеция, и какие у неё есть элементы.
Трапеция — выпуклый четырёхугольник, у которого две стороны параллельны, а две другие — не параллельны.
Параллельные стороны называют основаниями, а непараллельные — боковыми сторонами.Трапеции бывают прямоугольные, равнобедренные и простые.

В прямоугольных трапециях есть 2 прямых угла.
В равнобедренных трапециях, как в равнобедренных треугольниках, углы при основаниях равны, равны так же и боковые стороны.
В трапеции имеется средняя линия, которая соединяет середины боковых сторон.

А теперь задачи.

Острый угол равнобедренной трапеции равен 60°. Доказать, что основание ВС = AD — AB.
Доказательство.
Опустим из вершин трапеции высоты BM и CN на нижнее основание AD.
Получим два прямоугольных треугольника ABM и DCN, а также прямоугольник BCNM.
Поскольку в прямоугольных треугольниках один угол равен 60°, то второй, согласно следствию из теоремы о сумме внутренних углов треугольника,
равен 30°.
А мы знаем, что катет, лежащий против угла в 30°, равен половине гипотенузы.
Т.е. АМ= с/2.
То же самое и в правом треугольнике — ND = с/2.
Получается, что нижнее основание можно представить в виде суммы трёх отрезков, а именно AM, MN, ND, где AM=ND=c/2.
MN=BC, или верхнему основанию.
Отсюда можно написать MN=BC=AD — AM — ND = AD — c/2 — c/2 = AD — AB.
Мы доказали, что верхнее основание равно разности нижнего основания и боковой стороны.

Основания трапеции равны AD и BC. Найти длину отрезка KP, который соединяет середины диагоналей трапеции.
Решение:
На основании теоремы Фалеса отрезок KP принадлежит большему отрезку MN, который является средней линией трапеции.Средняя линия трапеции
, как мы знаем, равна полу-сумме оснований трапеции
, или (AD+BC)/2.
В то же время, рассматривая треугольник ACD и его среднюю линию KN, можно понять, что KN=AD/2.
Рассматривая другой треугольник BCD и его среднюю линию PN, можно увидеть, что PN=BC/2.
Отсюда, KP=KN-PN = AD/2 — BC/2 = (AD-BC)/2.
Мы доказали, что отрезок, который соединяет середины диагоналей трапеции, равен полу-разности оснований данной трапеции
.

Задача 3.
Найти меньшее основание ВС равнобедренной трапеции, если высота СK, проведённая из конца C меньшего основания, делит большее основание на отрезки AK и KD, разность которых равна 8 см.
Решение:
Сделаем дополнительное построение. Проведём высоту ВМ.
Рассмотрим треугольники ABM и DCK. Они равны по гипотенузе и катету
— AB=CD, как боковые стороны равнобедренной трапеции.
Высоты трапеции BM и CK тоже равны, как перпендикуляры, расположенные между двумя параллельными прямыми
.
Следовательно, AM=KD. Получается, что разность между AK и KD равна разности между AK и AM.
А это есть отрезок MK. Но MK равен ВС, поскольку BCKM — прямоугольник.Отсюда меньшее основание трапеции равно 8 см.

Задача 4.
Найти отношение оснований трапеции, если её средняя линия делится диагоналями на 3 равные части.
Решение:
Поскольку MN — средняя линия трапеции, то она параллельна основаниям и делит боковые стороны пополам
.
По теореме Фалеса MN делит также и стороны AC и BD пополам.
Рассматривая треугольник АВС можно видеть, что MO в нём — средняя линия. А средняя линия треугольника параллельна основанию и равна его половине
. Т.е. если MO=Х, то ВС=2Х.
Из треугольника ACD имеем ON — средняя линия.
Она тоже параллельна основанию и равна его половине.
Но, поскольку OP+PN= Х+Х=2Х, тогда AD=4Х.
Получается, что верхнее основание трапеции равно 2Х, а нижнее — 4Х.
Ответ: отношение оснований трапеции равно 1:2.

Всем выпускникам, которые готовятся к сдаче ЕГЭ по математике, будет полезно освежить в памяти тему «Произвольная трапеция». Как показывает многолетняя практика, планиметрические задачи из этого раздела вызывают у многих старшеклассников определенные сложности. При этом решить задачи ЕГЭ на тему «Произвольная трапеция» требуется при прохождении и базового, и профильного уровня аттестационного испытания. Следовательно, уметь справляться с подобными упражнениями должны все выпускники.