Порядок выполнения действий, правила, примеры

Порядок вычисления простых выражений

Существует четкое правило, определяющее порядок выполнения действий в выражениях без скобок:

• действия выполняются в порядке слева направо
• сначала выполняются умножение и деление, затем сложение и вычитание.

Из этого правила становится понятнее, какое действие выполняется первым. Универсального ответа нет, приходится разбирать каждый пример и выбирать решение самостоятельно.

Что первично, умножение или деление? — По порядку слева направо. Сначала умножение или сложение? Умножь и прибавь.

Порядок действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято писать слева направо. А необходимость сначала умножать или делить объясняется самой сутью этих операций.

Рассмотрим порядок арифметических действий в примерах.

Пример 1. Выполнить расчет: 11 − 2 + 5.

Как мы решаем:

В нашем выражении нет умножения, деления и скобок, поэтому все операции выполняем слева направо. Сначала вычтите два из одиннадцати:

11 — 2 = 9

Затем прибавляем к результату пять, и в итоге получаем четырнадцать:

9 + 5 = 14

Вот полное решение: 11 − 2 + 5 = 9 + 5 = 14.

Ответ: 14.

Пример 2. В каком порядке следует производить вычисления в выражении: 10 : 2 × 7 : 5?

Как мы спорим:

Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление, а значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Сначала делим десять на два:

10 : 2 = 5

Теперь умножьте результат на семь:

5 х 7 = 35

И полученное число делится на пять:

35 : 5 = 7

Запись всего решения выглядит так: 10 : 2 × 7 : 5 = 5 × 7 : 5 = 35 : 5 = 7.

Ответ: 7.

Пока не известны новые знания, чтобы не путать последовательность действий при вычислении значения выражения, числа удобно ставить над знаками арифметических действий, соответствующих порядку их выполнения.

Например, в такой последовательности можно решить пример с действиями:

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги – контрольЦенные бумаги – оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

Урок по математике 2 класс Порядок действий в выражениях со скобками.

Успейте воспользоваться скидками до 50% на курсы «Инфоурок»

Цель:
1.

2.

3. Закрепить знание таблицы умножения и деления на 2 – 6, понятия делителя и

4. Учить работать в парах с целью развития коммуникативных качеств.

Оборудование
* : + — (),
геометрический материал.

Раз, два – выше голова.

Три, четыре – руки шире.

Пять, шесть – всем присесть.

Семь, восемь – лень отбросим.

Но сначала придется узнать его название. Для этого нужно выполнить несколько заданий:

6 + 6 + 6 … 6 * 4 6 * 4 + 6… 6 * 5 – 6 14 дм 5 см… 4 дм 5 см

Пока мы вспоминали о порядке действий в выражениях, с замком происходили чудеса. Мы были только что у ворот, а теперь попали в коридор. Смотрите, дверь. А на ней замок. Откроем?

1. Из числа 20 вычесть частное чисел 8 и 2.

2. Разность чисел 20 и 8 разделить на 2.

— Чем отличаются результаты?

— Кто сможет назвать тему нашего урока?

(на массажных ковриках)

По дорожке, по дорожке

Скачем мы на правой ножке,

Скачем мы на левой ножке.

По тропинке побежим,

Наше предположение было полностью правильно7

Где выполняются действия сначала, если в выражении есть скобки?

Смотрите перед нами «живые примеры». Давайте «оживим» их.

* : + — ().

m – c * (a + d) + x

k: b + (a – c) * t

6. Работа в парах.

Для их решения вам понадобиться геометрический материал.

Учащиеся выполняют задания в парах. После выполнения проверка работы пар у доски.

Что нового вы узнали?

8. Домашнее задание.

Тема: Порядок действий в выражениях со скобками.

Цель:
1.
Вывести правило порядка действий в выражениях со скобками, содержащих все

4 арифметических действия,

2.
Формировать способность к практическому применению правила,

4.Учить работать в парах с целью развития коммуникативных качеств.

Оборудование
: учебник, тетради, карточки со знаками действий * : + — (),
геометрический материал.

1
.Физминутка.

Девять, десять – тихо сесть.

2. Актуализация опорных знаний.

Сегодня мы с вами отправляемся в очередное путешествие по стране Знаний городу математика. Нам предстоит посетить один дворец. Что-то я забыла его название. Но не будем расстраиваться, вы сами сможете мне подсказать его название. Пока я переживала, мы подошли к воротам дворца. Войдем?

1. Сравните выражения:

2. Расшифруй слово.

3. Постановка проблемы. Открытие нового.

Так как же называется дворец?

А когда в математике мы говорим о порядке?

Что вы уже знаете о порядке выполнения действий в выражениях?

— Интересно, нам предлагают записать и решить выражения (учитель читает выражения, учащиеся записывают их и решают).

20 – 8: 2

(20 – : 2

Молодцы. А что интересного в этих выражениях?

Посмотрите на выражения и их результаты.

— Что общего в записи выражений?

— Как вы думаете, почему получились разные результаты, ведь числа были одинаковые?

Кто рискнет сформулировать правило выполнения действий в выражениях со скобками?

Правильность этого ответа мы сможем проверить в другой комнате. Отправляемся туда.

4. Физминутка.

И по этой же дорожке

До горы мы добежим.

Стоп. Немножко отдохнем

И опять пешком пойдем.

5. Первичное закрепление изученного.

Вот мы и пришли.

Нам нужно решить еще два выражения, чтобы проверить правильность нашего предположения.

6 * (33 – 25) 54: (6 + 3) 25 – 5 * (9 – 5) : 2

Для проверки правильности предположения откроем учебники на стр. 33 и прочитаем правило.

Как нужно выполнять действия после решения в скобках?

На доске написаны буквенные выражения и лежат карточки со знаками действий * : + — ().
Дети выходят к доске по одному, берут карточку с тем действием, которое нужно сделать сначала, потом выходит второй ученик и берет карточку со вторым действием и т. д.

а + (а –в)

а * (в +с) :
d
–
t

m
–
c
* ( a
+
d
) +
x

k
b
+ ( a
–
c
) *
t

(a – b)
t + d

6. Работа в парах.
Автономная некоммерческая организация Бюро судебных экспертиз
Судебная экспертиза. Несудебная экспертиза
Рецензия на экспертизу. Оценка
Автономная некоммерческая организация «Бюро судебных экспертиз» в Москве – центр

Особенности бухгалтерского учета субсидий
Государство стремится поддержать малое и среднее предпринимательство. Такая поддержка наиболее часто выражается в форме предоставления субсидий – безвозмездных выплат из
Жалоба на педиатра
Жалоба на педиатра — официальный документ, устанавливающий требования пациента и описывающий суть возникновения таких требований. Согласно статье 4 Федерального закона «О порядке рассмотрения
Ходатайство об уменьшении размера исковых требований
Один из видов уточнения иска — ходатайство об уменьшении размера исковых требований. Когда истец неправильно определил цену иска. Или ответчик частично исполнил

Стратегии решения математических задач

Математические задачи со словами могут быть сложными и часто сложными для решения. Использование метода SQRQCQ может сделать решение математических задач проще и менее пугающим. Метод SQRQCQ особенно полезен для детей с ограниченными возможностями обучения и может эффективно использоваться в программах специального образования. SQRQCQ — это сокращение от Survey, Question, Read, Question, Compute и Question.

Шаг 1 — ОПРОС по математической задаче

Первый шаг к решению задачи по математическому слову — прочитать задачу полностью, чтобы понять, что вас просят решить. После прочтения вы сможете определить наиболее важные аспекты проблемы, которые необходимо решить, и какие аспекты не имеют отношения к решению проблемы.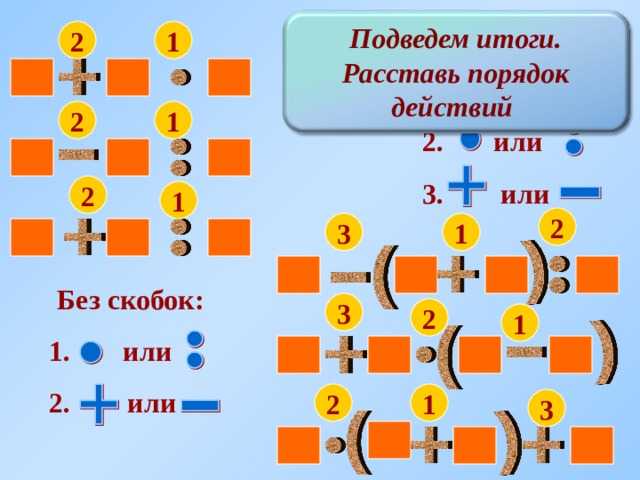

Шаг 2 — ВОПРОС

Как только у вас появится представление о том, что вы пытаетесь решить, вам нужно определить, какие формулы, шаги или уравнения следует использовать, чтобы найти правильный ответ. Невозможно найти ответ, если вы не можете определить, что нужно решить. В основном, какие вопросы задает проблема?

Шаг 3 — ПОВТОРНО ПРОЧИТАТЬ

Теперь, когда вы определили, что нужно решить, перечитайте задачу и обратите пристальное внимание на конкретные детали. Определите, какие аспекты проблемы взаимосвязаны

Определите все соответствующие факты и информацию, необходимые для решения проблемы. Как вы это сделаете, запишите их.

Шаг 4 — ВОПРОС

Теперь, когда вы знакомы с конкретными деталями и тем, как взаимосвязаны различные факты и информация в задаче, определите, какие формулы или уравнения необходимо использовать для постановки и решения задачи. Обязательно запишите, какие шаги или операции вы будете использовать для удобства.

Шаг 5 — ВЫЧИСЛЕНИЕ

Используйте формулы и/или уравнения, указанные на предыдущем шаге, для завершения вычислений. Обязательно следуйте описанным шагам при настройке уравнения или использовании формулы. По мере выполнения каждого шага отмечайте его в своем списке.

Шаг 6 — ВОПРОС

После того, как вы завершили расчеты, просмотрите окончательный ответ и убедитесь, что он правильный и точный. Если это не кажется логичным, просмотрите шаги, которые вы предприняли, чтобы найти ответ, и поищите ошибки в расчетах или настройке. Пересчитайте числа или внесите другие изменения, пока не получите ответ, который имеет смысл.

Как SQRQCQ помогает учащимся с ограниченными возможностями обучения?

Математические задачи со словами, как правило, особенно сложны для учащихся с ограниченными возможностями обучения (LD). Студентам LD часто не хватает «концептуального образа» или способности визуализировать всю проблему, создавая полный мысленный образ.

Ученики LD также могут испытывать трудности с правильным пониманием слов или формулировок в задачах по математике. Неспособность правильно интерпретировать и понимать формулировки сильно влияет на их навыки математического мышления и часто приводит к неверным расчетам и неверным выводам.

Запоминание и обработка информации и деталей в рабочей памяти — еще одна проблема, с которой сталкиваются учащиеся LD, когда они пытаются увидеть картину целиком. Медленная обработка информации, сопровождаемая разочарованием и беспокойством, часто приводит к тому, что учащиеся с ограниченными возможностями стараются решить математические задачи как можно быстрее, поэтому они часто сразу же переходят к вычислениям, пытаясь добраться до финиша как можно быстрее. насколько это возможно.

SQRQCQ — это метакогнитивное руководство, которое предоставляет учащимся LD логический порядок решения математических задач.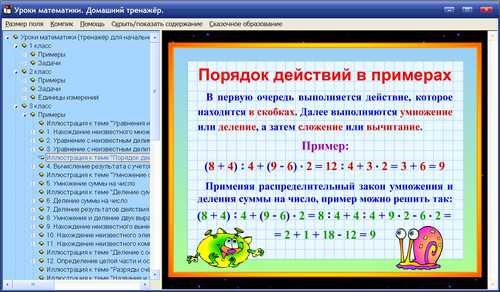

Экспоненты, умножение и сложение – MathFour

Рубрики: Алгебра; Будьте первым, кто поделится своими мыслями — оставьте комментарий ниже!

Это четвертая книга из серии Объяснение порядка действий. Чтобы ознакомиться с другими статьями этой серии, нажмите здесь, чтобы перейти к введению.

Порядок операций можно свести к трем «настоящим» операциям.

Скобки — это просто способ сгруппировать элементы, а не настоящая операция. Поэтому они не считаются реальной операцией.

Поскольку деление — это просто умножение, перевернутое с ног на голову, нам не нужно включать его отдельно. Точно так же вычитание — это сложение на слуху. Так что его тоже выкидываем.

Теперь у нас есть только три: показатели степени, умножение и сложение.

Экспоненты — это ярлык для умножения.

В предыдущей статье о запоминании правил экспоненты я записал это видео о экспонентах:

Вы видите, что 3 x 3 x 3 x 3 равно 3 4 . Экспонента — это сокращение для умножения.

Умножение — это быстрый способ сложения.

Точно так же, когда мы перегружены сложением одних и тех же чисел снова и снова, как в видео, 4 + 4 + 4 + 4 + 4, мы можем использовать умножение, чтобы сократить это: 5 x 4.

Следуйте сокращению эволюция.

Эволюция быстрого доступа выглядит следующим образом:

1. Сначала появилось дополнение.
2. Затем мы создали умножение, чтобы упростить сложение.
3. Затем мы создали показатели степени, чтобы упростить умножение.

Итак, когда вы занимаетесь арифметикой, мы должны сначала использовать «недавние» сокращения (возведение в степень), затем «старые» сокращения (умножение), а затем «обычные» арифметические действия (сложение). Помните, что вычитание — это сложение, а деление — это умножение.

И имейте в виду, что нам нужно следить за группировкой или чем-либо изолированным скобками, барами абсолютного значения или дробью. Инструменты группировки/изоляции всегда важнее других правил работы.

Что, если ваш ответ не совпадает с ответом на обратной стороне книги?

В некоторых учебниках умножение выполняется перед делением.

Порядок операций — это набор правил, которые мы согласовали. Это означает, что пока учебник четко определяет их порядок, которому они будут следовать, они могут делать такие вещи.

Если вы не знаете, что делать первым, потребуйте скобки. (Да, вы можете это сделать.) Или поставьте круглые скобки в учебнике вашего ребенка, чтобы помочь ему.

Наборы задач должны быть там, чтобы обеспечивать, а не путать.

Этот пост может содержать партнерские ссылки. Когда вы используете их, вы поддерживаете нас, чтобы мы могли продолжать предоставлять бесплатный контент!

Закономерности и приоритеты операций

В математике существуют определенные законы и приоритеты, которые регулируют порядок выполнения операций. Соблюдение этих закономерностей позволяет получать корректные и однозначные результаты.

Приоритет операций:

1. Скобки: выражения в скобках имеют наивысший приоритет и вычисляются первыми.
2. Умножение и деление: операции умножения и деления выполняются вторыми после скобок и имеют одинаковый приоритет.
3. Сложение и вычитание: операции сложения и вычитания выполняются последними и имеют одинаковый приоритет.

Примеры:

1) Рассмотрим выражение: 5 + 3 * 2. Сначала выполняется умножение: 3 * 2 = 6. Затем производится сложение: 5 + 6 = 11.

2) Рассмотрим выражение: (8 — 4) / 2. Выполняется вычитание в скобках: 8 — 4 = 4. Затем производится деление: 4 / 2 = 2.

Ассоциативность операций:

В случае, когда в выражении есть несколько операций с одинаковым приоритетом, они выполняются слева направо (левоассоциативность).

Пример:

Рассмотрим выражение: 8 — 4 + 2. Вычитание и сложение имеют одинаковый приоритет. По ассоциативности операций, вычитание будет выполнено первым: 8 — 4 = 4. Затем производится сложение: 4 + 2 = 6.

Закономерности:

1. Закон коммутативности: операции сложения и умножения могут быть переставлены местами без изменения результата.
2. Закон ассоциативности: результат операций сложения и умножения не зависит от того, в каком порядке они выполняются.
3. Закон дистрибутивности: умножение разности на число равно разности произведений этого числа на вычитаемое и умножаемое число.

Примеры:

1) Закон коммутативности умножения: 3 * 2 = 2 * 3 = 6.

2) Закон ассоциативности сложения: (2 + 3) + 4 = 2 + (3 + 4) = 9.

3) Закон дистрибутивности: 2 * (3 — 1) = (2 * 3) — (2 * 1) = 4.

Важно следовать закономерностям и приоритетам операций, чтобы получать правильные результаты при решении математических задач и вычислениях

Дробная черта

Дробную черту в выражении можно заменить знаком деления, в этом случае все, что было выше и ниже дробной черты, необходимо заключить в круглые скобки. Например:

13+2	= (13 + 2): (10 — 7).
10 — 7

Знак деления в выражении может быть заменен дробной косой чертой только в том случае, если это не нарушает порядок действий. Например, выражение:

20: 4(2+3)

не может быть заменен на

20	,
4(2+3)

потому что такая замена нарушила бы порядок операций в этом выражении.

<td> ;

20: 4(2+3) ≠	20
4(2+3)

20	= 20: (4(2 + 3)).
4(2+3)

Дробная черта в выражении заменяет скобки и означает, что необходимо вычислить отдельно выражение в числителе и отдельно выражение в знаменателе, и разделить первый результат на второй.

Справочная информация

ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

1. Перенесем 6x из левой части в правую. Знак меняем на противоположный, то есть минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

1. Сократим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах. Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет

Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Алгоритм решения простого линейного уравнения
Раскрываем скобки, если они есть. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую. Приводим подобные члены в каждой части уравнения. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе.

А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе.

Правило встречается в следующих упражнениях:

2 класс

Страница 17,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 23,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 44,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 48,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 52,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 58,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 59,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 110,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 54,
Моро, Волкова, Рабочая тетрадь, часть 2

3 класс

Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 53,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 110,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 9,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 27,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 74,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 102,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 17,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 45,
Моро, Волкова, Рабочая тетрадь, часть 2

4 класс

Страница 12,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 30,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 45,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 80,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 9. Вариант 2. Проверочная работа 2,
Моро, Волкова, Проверочные работы

Страница 28,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 31,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 59,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

5 класс

Задание 30,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 98,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Упражнение 244,
Мерзляк, Полонский, Якир, Учебник

Упражнение 260,
Мерзляк, Полонский, Якир, Учебник

Упражнение 456,
Мерзляк, Полонский, Якир, Учебник

Упражнение 596,
Мерзляк, Полонский, Якир, Учебник

Упражнение 5,
Мерзляк, Полонский, Якир, Учебник

Упражнение 838,
Мерзляк, Полонский, Якир, Учебник

Упражнение 920,
Мерзляк, Полонский, Якир, Учебник

Упражнение 6,
Мерзляк, Полонский, Якир, Учебник

6 класс

Задание 85,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 92,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 373,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 378,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 400,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 411,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 422,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 425,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 445,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 454,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Примеры по математике со скобками

Выполнение тех или иных операций предполагает определённый порядок действий.

Если производить действия в порядке их записи, четыре минус два плюс один, результат будет равен трём. Если же вначале сложить 2 и 1 и вычесть данную сумму из 4 , то получится цифра 1 .

Чтобы указать, в каком порядке нужно выполнять действия применяют Скобки.

Действия, заключенные в Скобки, выполняются раньше других.

( 3 + 4 ) × 5 = 7 × 5 = 35

4 + ( 4 × 5 ) = 4 + 20 = 24

Скобки не ставятся в тех случаях если:

1 . действия сложения и вычитания, исполняются в последовательности, как они записаны:

Вместо ( 6 – 2 ) + 1 = 5 пишут 6 – 2 + 1 = 5

2 . внутри Скобок совершаются операции умножения или деления:

Вместо 2 + ( 2 × 8 ) = 18 пишут 2 + 2 × 8 = 18

При расчёте таких выражений, которые либо вовсе не содержат разделительных скобок, либо имеют такие скобки, внутри которых не содержится других скобок, следует производить действия в следующем порядке:

1 . вначале выполняются операции с цифрами заключенными в скобки, при этом действия умножения и деления делаются в порядке их следования, но ранее, чем сложение и вычитание.

2 . Затем, исполняются остающиеся действия, причем опять умножение и деление производятся в порядке их следования, но ранее сложения и вычитания.

Сначала выполняется умножения

Затем выполняется вычитание

22 + 16 : 4 – 4 × ( 17 – 2 × 7 + 3 ) + 7 × ( 3 + 4 )

Выполнение действий в скобках:

17 – 2 × 7 + 4 = 17 – 14 + 3 = 6

Выполнение остающихся действий:

22 + 16 : 4 – 4 × 6 + 7 × 7 = 22 + 4 – 24 + 49 = 51

Зачастую для указания порядка действий, необходимо применять дополнительные скобки.

Тогда, кроме простых круглых скобок, используют скобки иной формы:

Вычисление этих выражений реализуется в следующем порядке:

Вначале операции вычисления производятся внутри всех круглых скобок

Затем – вычисления внутри всех квадратных скобок

Далее – вычисления внутри фигурных скобок

После выполняются остающиеся действия

5 + 2 × + 36 : ( 12 – 2 × 3 )

Выполнение действий в круглых скобках:

12 – 2 × 3 = 12 – 6 = 6

Действия в квадратных скобках:

Выполнение остающихся действий:

5 + 2 × 6 + 36 : 6 = 5 + 12 + 6 = 23