Javascript array.filter() tutorial

Availability in modern browsers #

Right now a number of the CSS effects are being made available in WebKit based browsers and Mozilla. We expect to see them soon in Opera as well as IE10. As the specification is still under development, some browser vendors have implemented this stuff using vendor prefixes. So in WebKit you need to use , in Mozilla you will need to use and keep your eye out for other browser implementations as they appear.

Not all browsers will support all filter effects right away, so your mileage will vary. Presently, the Mozilla browser supports only the function — without the vendor prefix, as that implementation pre-dates the other effects functions.

We’ve summarized the CSS filter effects available in the various browsers below with rough performance indicators for when they’re implemented in software. Note, that a number of modern browsers are beginning to implement these in hardware (GPU accelerated). When these are built with GPU support, performance will be greatly improved for the slower effects. As usual, testing on different browsers is the best way to evaluate the performance.

Filter effect	Browser support	Performance
grayscale	Chrome	very fast
sepia	Chrome	very fast
saturate	Chrome	very fast
hue-rotate	Chrome	fast
invert	Chrome	very fast
opacity	Chrome	can be slow
brightness	Chrome	fast
contrast	Chrome	fast
blur	Chrome	slow unless accelerated
drop-shadow	Chrome	can be slow
url()	Chrome, Mozilla	Varies, fast to slow

How to Use the Array Filter Method

Now that you understand the behavior of the method and its final result, we are going to learn how to use the method in JavaScript.

Note: Remember: the method will be available as long as there is an array instantiated.

Understanding the Syntax

First, let’s understand the syntax of the method. The filter method accepts two arguments, a and or the value of inside the callback function. We are going to explain later argument to keep things simple.

As you noticed, there are two syntaxes to use the method. Using the argument is required. Using the is optional. Hence, it is enough if we only provide the parameter.

The is a callback function that accepts up to three parameters: , , .

Let’s understand what each of these parameters is:

• The is the current element in the original array (required parameter).
• The is the position of the or current element in the original array (optional parameter).
• The is the original array (optional parameter).

This leaves us with four different syntaxes you can use when using the method.

Using the Method without

It is typical to use the method without the . Let’s look at how to use method without it.

1. First, create an array that we are going to use the method.

2. Second, apply the method in the array created in the previous step. Add the logic desired to filter elements of the original array. In this case, we are going to get only elements with the text equal to “triangle”.

3. Assign a variable the filtered array result.

Defining a Callback Function without Optional Paramaters

In the previous example, we had defined a callback function with its three parameters.

However, we didn’t use the and parameters in the callback function. We can rewrite the callback function without those two parameters and it will still work.

Defining a Callback Function using parameter

Let’s say we want to get only a certain number of elements from the original array instead of filtering by triangles. We can use the parameter of the callback function to get the top 3 elements of the original array.

Remember, the index number in an array starts with for the first element of the array. Hence, if we want to get the top three elements of an array, the index of the third element in an array will be .

Result of Array Filter Method With Callback using Index Parameter

Defining a Callback Function using parameter

If you have the original array assigned to a variable, there wouldn’t be any need to use the third argument.

You can also apply the method without necessarily assigning a variable to the original array.

In this case, there is no variable assigned to the array if we want to use the original array for additional logic inside the callback function. This is when it becomes handy to use the third parameter to have access to that original array becomes handy

Assigning a Variable to a Filter Callback Function

Another possibility is to define the callback function inside a variable and pass that variable as a parameter when calling the method. This allows reusing a callback function as we don’t always know the array using the method.

In these examples, we are not really using the third argument besides logging the original array, which it isn’t part of the logic determining what filtered values to get. We can say we want to get half of the elements of an array. In that case, we can use the original array to get the total elements in filter the elements based on the index value.

More JavaScript Array filter() method examples

Because the method returns a new array, you can chain the result with other array methods such as and .

For example, the following illustrates how to chain the three methods: and

Output:

How it works.

• First, filter the cities whose populations are less than 3 million using the method.
• Second, sort the resulting cities by the populations in descending order using the method.
• Third, output array element to the console using the method.

The following example illustrates the use of the argument that specifies an object which can be referenced in the function using the keyword

Output:

How it works.

• First, define the function that checks if its argument is a number and in the range specified by the and properties of an object.
• Next, define an array of mixed data that contains , , and .
• Then, define the object with two properties and .
• After that, call the methods of the array and pass in the function and the object. Because we pass in the object, inside the function, the keyword references to the object.
• Finally, show the result array in the console.

In this tutorial, you have learned how to use the JavaScript Array method to filter elements in an array based on a test provided by a callback function.

Window type

The window defines the behaviour of the filter in the transition and the stopband (the height of the sidebands and the width of the main band).

Blackman — when more dynamic range is needed (we want to see a very small signal among large ones), Blackman window is a better choice because sidebands are 10 times lower than with the Hanning window. However, the sideband width is wider. Here it comes to the point — if more lines in FFT are chosen, we can use these windows and still larger sidebands have no real disadvantage.

Rectangular — the rule of thumb is when we want a pure transformation with no window’s side effects (for advanced calculations), we should use a Rectangular window (which is, by the way, equal to no window).

Hamming, Hanning — for general purpose, Hamming or Hanning windows are commonly used because they provide a good compromise between falloff and amplitude error (maximum of 15%). This comes from the fact that old frequency analysers didn’t have that many possibilities in terms of frequency lines and these two windows have narrow sideband.

Flat top — if correct amplitudes are searched, we should use the flat-top window. The amplitudes would be wrong by only a fraction (as low as 1%). Of course, there is a penalty — neighbour frequencies are also very high (sideband width is high). Flat top window is most suitable for calibration. But here it is the same: with modern equipment with lots of lines, this is no longer that much of a problem.

Wrapping Up!

In this detailed guide on filter in Python, you looked into the basics of the filter method which is used to filter elements from an iterable based on a function. This article also discussed some typical applications of the filter method along with the syntax and the parameters. Then, you moved forward and explored some useful examples where one would use the filter method with lambda functions, custom functions, and even with None option on different iterables like lists, list of dictionaries, etc.

If you are looking for the most effective way to this tech industry of web development, a great way to start would be to enroll in the comprehensive Python Training Course. With this course, you will gain all the practical and work-ready skills you’d need to be employable and grab the best opportunities for you in the field. 

Hope that you now have hands-on experience working with the Filter method in Python. Do you have any questions for us? Leave them in the comments section of this article, and our experts will answer them for you at the earliest!

Как работает filter() с функцией

Первый аргумент filter() – это функция, которая позволит нам включить или отфильтровать те или иные элементы. Функция вызывается один раз для каждого элемента в итерируемом объекте, который передается в качестве второго аргумента. Каждый раз, когда функция возвращает False, значение сбрасывается. В качестве первого аргумента можно либо передать обычную функцию, либо использовать лямбда-функцию (особенно если выражение менее сложное).

Ниже приведен синтаксис лямбды с filter():

Допустим, у нас есть приведенный ниже список – это список имен рыбок, которые живут в нашем аквариуме. Тогда мы можем включить лямбда-функцию с выражением, по которому мы хотим оценивать каждый элемент из этого списка:

Чтобы отфильтровать этот список и отобрать только имена, которые начинаются с гласной, мы можем запустить следующую лямбда-функцию:

Здесь мы объявили элемент в списке как x. Далее мы открываем выражению доступ к первому символу каждой строки (или к нулевому символу), поэтому мы получаем x . Устанавливая нижний регистр для каждого имени, мы можем быть уверены, что буквы будут соответствовать выражению ‘aeiou’.

Затем мы передаем итерируемый объект creature_names. Как и в предыдущем примере, мы применяем к результату функцию list(), чтобы создать список из итератора, возвращаемого функцией filter().

В итоге мы получим:

Того же результата можно достичь с помощью функции, которую мы определяем:

Функция names_vowels определяет выражение, с помощью которого можно отфильтровать creature_names.

Мы получим такой же результат:

В целом лямбда-функции в сочетании с функцией filter() дают такой же результат, что и обычная функция. Чем сложнее выражение для фильтрации данных, тем лучше использовать при этом обычную функцию – это, вероятно, будет способствовать читаемости кода.

Prototypes of filters:

Butterworth — Butterworth is without the ripple and maintains the shape with higher orders. Roll-off is defined with (-20 dB/decade)*order. It is also known as maximally flat magnitude, suggesting that the filter response is really flat in the passband.

Chebyshev I — sometimes the selection of the filters is defined by the application, but in general, the Chebyshev has the highest roll-off of all three, but has a ripple in the passband and doesn’t maintain the shape with higher orders.

Bessel — Bessel filter is the filter with maximally linear phase response. The roll-off, however, is the least steep of all three filter types.

The Syntax For Filter in Python

The syntax for the filter() function in Python is — 

filter(function, iterable)

The two parameters are the following — 

1. Function — It works on each element of the iterable and tests whether the returned value is true or false. The output sequence will contain all those elements of the iterable for which the function has returned True. It can also be mentioned as None. In such a case, the output sequence will simply contain all those elements that satisfy the boolean condition True.
2. Iterable — It is the iterable or the list of items on which the filtering is to be performed on. An iterable can be a set, list, tuple, dictionary, etc.

The filter() method in Python will return an iterator that will contain all the elements of the original iterable that has passed the function check.

Using filters

Let’s find out why we should even use filters. For this example, I have a tuning fork instrumented with strain gage connected on Dewesoft measuring device SIRIUS.

Image 8: DAQ device with strain gage sensor mounted on a tuning fork

When the tuning fork is connected to the STG module, it can be seen in Measure mode under Channel setup screen’s Analog in section.

Image 9: Analog in channel setup

If you take a look at the recorder when a static force is applied on the tuning fork, you can see the changing offset of the signal.

You might also try hitting the tuning fork so it makes a sound that is reflecting the natural frequency of the tuning fork (the conventional way it is used). You can see a high-frequency vibration with falling amplitude because of air friction and friction in the fork.

Image 10: Signal of different forces applied to the tuning fork

When looking at the FFT screen (change it to the logarithmic scale to see all the amplitudes), you can see that there is an obvious peak at approximately 440 Hz. You can also place a cursor at this point by simply clicking on the peak in the FFT. The frequency shown is 439.5 Hz. It is not exactly 440 Hz because FFT has a certain line resolution.

This line resolution depends on the sampling rate and the number of lines chosen for the FFT. If you want to have a faster response on the FFT, we would choose fewer lines, but you would have a lower frequency resolution. If on the other hand, you want to see the exact frequency, it is necessary to set a higher line resolution. This is well described in the reference guide, but a simple rule of thumb is: if it takes 1 second to acquire the data from which the FFT is calculated, the resulting FFT will have 1 Hz line resolution. If you acquire data for 2 seconds, line resolution will be 0.5 Hz.

Image 11: FFT and time signal of the vibrating tuning fork

This is also a perfect example to learn about using the filters in Dewesoft X. Clearly, there is one part of the signal in the form of the offset (static load) and one part in a form of dynamic ringing with a 440 Hz frequency.If you want to extract those two components from the original waveform, you need to set two filters — one low pass and one high pass. 

To achieve this add two filters in the Channel setup’s Math module.

Image 12: Math made filters

1. Setting the 1st filter

• Set by selecting the input channel, in this case, Tuning fork
• Leave Design type at Preset
• In Design parameters confirm that the Prototype is set to Butterworth and set the number of Orders to 6.
• Set the Frequencies filter Type to Low pass, and update Fc2 to 200Hz

This filter will pass all the signals below 200Hz frequency. All the frequencies above 200Hz will be cut off.

2. Setting the 2nd filter 

• Set by selecting the input channel, again to, Tuning fork
• Leave Design type at Preset
• In Design parameters confirm that the Prototype is set to Butterworth and set the number of Orders to 6.
• Set the Frequencies filter Type to High pass, and update Fc1 to 200Hz

This filter will block all the signals below 200Hz frequency and pass by all signals above 200Hz.

If you display those two filters on the recorder, you can see that the signal is nicely decomposed to the static load and dynamic ringing. You can use this technology to cut off unwanted parts of the signal or to extract wanted frequency components of the certain signal.

Image 13: Comparison of RAW, Low-pass filtered and High-pass filtered time signals

Introduction to Filter in Python

Filter() is a built-in function in Python. The filter function can be applied to an iterable such as a list or a dictionary and create a new iterator. This new iterator can filter out certain specific elements based on the condition that you provide very efficiently. 

Note: An iterable in Python is an object that you can iterate over. It is possible to loop over an iterable and return items that are in it.

There are many ways to filter elements from a list. This includes using a simple for loop, list comprehension, advanced for loop, etc. However, the filter method provides a simple and efficient way to filter out elements and even takes fewer lines of code to carry out the same function. This is very useful especially when you are working with large sets of data. 

Consider this simple scenario. Suppose, you have a list of books that contains details of more than 1000 books. Now, if you try to use a comprehensive function to filter out specific books, the process can be quite exhaustive in terms of resource utilization. The comprehensive list will create a new list and by the time it has completed its entire operation, you will have two lists in our memory. And when the lists are very large, this can cause a huge problem. Moreover, it increases the overall runtime of the processing. 

In contrast to this, the filter() function will simply make an object which will not be a copy of the list but will be a reference to the original list, along with the function that has been provided to filter, and the indices which have to be traversed in the original list. Needless to say, this takes less memory and executes faster than list comprehension. 

JavaScript Array filter() method in detail

The following illustrates the syntax of the method:

The method creates a new array with all the elements that pass the test implemented by the function.

Internally, the method iterates over each element of the array and passes each element to the  function. If the  function returns , it includes the element in the return array.

The method accepts two named arguments: a  function and an optional object.

Like other iterative methods of the Array object such as and the  function has the following form:

The function takes three arguments:

• The argument is the current element in the array that is being processed by the function.
• The of the that is being processed by the function.
• The object being traversed.

The and arguments are optional.

The argument of the method is optional. If you pass the value, you can reference it by using keyword inside the  function.

It is important to note that the method does not change the original array.

Derivation

The derivative of a function of a real variable measures the sensitivity to change of a quantity (a function or dependent variable) which is determined by another quantity (the independent variable).

For example, the derivative of the position of a moving object with respect to time is the object’s velocity: this measures how quickly the position of the object changes when time is advanced.

The derivative of a function can be geometrically interpreted as the slope of the curve of the mathematical function f(x) plotted as a function of x. But its implications for the modelling of nature go far deeper than this simple geometric application might imply. Its importance lies in the fact that many physical entities such as velocity, acceleration, force and so on are defined as instantaneous rates of change of some other quantity. The derivative can give you a precise instantaneous value for that rate of change and lead to precise modelling of the desired quantity.

The derivate of the function f(x) evaluated at x=a gives the slope of the curve at x=a.

Image 53: Visual representation of derivation

Performance considerations #

One thing that every web developer cares about is performance of their web page or application. CSS filters are a powerful tool for visual effects, but at the same time might have an impact on the performance of your site.

Understanding what they do and how this affects performance matters, especially if you want your site to work well on mobile devices if they support CSS filters.

Firstly, not all filters are created equal! In fact, most filters will run really quickly on any platform and have very minor performance impact. However, filters that do any kind of blurring tend to be slower than the others. This of course means ‘blur’ and ‘drop-shadow’. This doesn’t mean you shouldn’t use them but understanding how they work might help.

When you do a , it mixes the colors from pixels all around the output pixel to generate a blurred result. So, say if your parameter is 2, then the filter needs to look at 2 pixels in every direction around each output pixel to generate the mixed color. This happens for each output pixel, so that means a lot of calculations that just get bigger when you increase the . Since looks in every direction, doubling the ‘radius’ means you need to look at 4 times as many pixels so in fact it’s 4 times slower for each doubling of the . The filter contains a as part of its effect, so it too behaves just like when you change the and parts of the parameter.

All is not lost with since on some platforms it’s possible to use the GPU to accelerate it, but that’s not necessarily going to be available in every browser. When in doubt the best thing is to experiment with the ‘radius’ that gives you the effect you want, then try to reduce it as much as possible while still maintaining an acceptable visual effect. Tuning this way will make your users happier especially if they use your site from a phone.

If you’re using based filters that reference SVG filters, they can contain any arbitrary filter effect so be aware that they too could be slow, so try to make sure you know what the filter effect does and experiment on a mobile device to make sure the performance is OK.

Пример использования

В следующем примере с использованием JavaScript метода .filter() мы рассмотрим как получить новый массив, который содержит элементы больше 50:

var array = ; // инициализируем переменную, содержащую массив числовых значений 

var filtered = array.filter( // вызываем переданную функцию один раз для каждого элемента массива, формируя новый массив
  function checkNumber( currentValue ) {
    return currentValue > 50;
  }
);
// аналогично с использованием стрелочной функции
let filtered = array.filter( currentValue => currentValue > 50 );

console.log( filtered ); // выводим значение переменной filtered равное 

В следующем примере мы рассмотрим использование второго аргумента метода .filter(), который указывает на объект, на который мы можем ссылаться с использованием ключевого слова this внутри функции обратного вызова:

var array = ; // инициализируем переменную, содержащую массив числовых значений 
var myObject = { // инициализируем переменную, содержащую объект 
  test: function( currentValue ) { // метод объекта, который принимает значение  
    return currentValue  50; //  возвращаем логическое значение, определяющее результат проверки 
  }
};

var filtered = array.filter( // вызываем переданную функцию один раз для каждого элемента массива, формируя новый массив
  function( currentValue ) {
    return this.test( currentValue ); //  возвращаемое значение метода test объекта myObject
  }, myObject // объект, на который мы ссылаемся с использованием ключевого слова this 
);

console.log( filtered ); // выводим значение переменной squared равное 

JavaScript Array

Filter an Array of Objects by Value

Filtering an array of objects based on the value of the properties or keys is a common task you will run into when working on projects. Luckily is not much different than working with other types of values as long as you define the property used to filter the array. For example, if we want to get only the cars made in the current year, you can access the property for each element and run the conditional logic.

At this point, everything looks good. However, we could make a minor modification in the name used for the first parameter to name it to something that represents better the elements of the array instead of calling it . We are going to rename the parameter as .

Window

Window Object
addeventlistener()
alert()
atob()
blur()
btoa()
clearInterval()
clearTimeout()
close()
closed
confirm()
console
defaultStatus
document
focus()
frameElement
frames
history
getComputedStyle()
innerHeight
innerWidth
length
localStorage
location
matchMedia()
moveBy()
moveTo()
name
navigator
open()
opener
outerHeight
outerWidth
pageXOffset
pageYOffset
parent
print()
prompt()
removeEventlistener()
resizeBy()
resizeTo()
screen
screenLeft
screenTop
screenX
screenY
scrollBy()
scrollTo()
scrollX
scrollY
sessionStorage
self
setInterval()
setTimeout()
status
stop()
top

Window Console
assert()
clear()
count()
error()
group()
groupCollapsed()
groupEnd()
info()
log()
table()
time()
timeEnd()
trace()
warn()

Window History
back()
forward()
go()
length

Window Location
assign()
hash
host
hostname
href
origin
pathname
port
protocol
reload()
replace()
search

Window Navigator
appCodeName
appName
appVersion
cookieEnabled
geolocation
javaEnabled()
language
onLine
platform
product
taintEnabled()
userAgent

Window Screen
availHeight
availWidth
colorDepth
height
pixelDepth
width

Comparing analogue and digital filters

Analogue filters are much more subjected to non-linearity (resulting in smaller accuracy) because the electronic components that are used for filtering are inherently imperfect and often have values specified to a certain tolerance limit (resistors often have a tolerance of ±5% ). This can be further affected by temperature and time changes. The elements of the circuits also introduce thermal noise, because every element is subject to heating. As we might expect, the more complex the circuit, the greater the magnitude of component errors. On top of that, analogue filters cannot have a FIR response because it would require delay elements.

But where they shine is high-frequency filtering, low latency, and speed. Like it was mentioned in the converter section, a digital filter can not work without preemptive anti-alias filtering, which can only be achieved with a low-pass analog filter. The speed of the analog filter can easily be 10 to 100 times that of a digital one. Also worth mentioning is that in very simple cases, an analog filter surpasses its digital counterpart in terms of cost efficiency.

The digital filter shines in a lot of areas where the analog does not. It is more accurate, supports both IIR and FIR, it can be programmed, making them easier to build and test while giving them greater flexibility. It’s also more stable since it isn’t affected by temperature and humidity changes. They are also far superior in terms of cost efficiency, especially as the filter gets more complex.

The downsides of digital filters are latency because the signal has to go through two converters and still be processed at high frequencies. In today’s modern circuits, both filters are used to complement each other and achieve maximum speed and accuracy.

A comparison of digital and analog filters:

How filters work #

So what does a filter do exactly? The easiest way to think of a filter is as a post processing step that does something magical after all your page content has been laid out and drawn.

When a browser loads a web page it needs to apply styles, perform layout and then render the page so there’s something to look at. Filters kick in after all those steps and just before the page is copied to the screen. What they do is take a snapshot of the rendered page as a bitmap image, then perform some graphics magic on the pixels in the snapshot and then draw the result over the top of the original page image. One way to think of them is like a filter placed on the front of a camera lens. What you’re seeing through the lens is the outside world modified by the effect of the filter.

This of course means that there’s time consumed when drawing a page with filters on it, but using them properly will have minimal impact on the speed of your site.

Also, just as you can stack a number of filters in front of each other on your camera lens, you can apply an arbitrary number of filters one after the other to achieve all sorts of effects.

Cut-off frequency

The filter cutoff frequency defines the -6 dB point (half amplitude) of the filter. You can enter Cut-off frequency in the field:

Fc1 (Low frequency) — You can enter Low for Low pass, Bandpass and Bandstop filter.

Fc2 (High frequency) — You can enter High for High pass, Bandpass and Bandstop filter.

Fc1 and Fc2 — You can enter Fc1 and Fc2 for Bandpass and Bandstop filter.

Fc1 value must be always lower than Fc2. These values are limited by filter stability. In Dewesoft X, the filters are calculated in sections, which enable the ratio between cutoff and sample frequency in a range of 1 to 100000. So we are able to calculate 1 Hz high pass filter with 100 kHz sampling rate.

Digital filter

A digital filter is a signal processing system that performs mathematical operations on a sampled (a continuous signal that has been reduced to a discrete one), discrete-time (unlike the continuous signal, the discrete one does not have a value at every instance of time — it is quantized ), digital (a physical signal that is a representation of a sequence of discrete values — for example, an arbitrary bit stream or a digitized analog signal) signal.

It is used in the same way as analogue filters. They are used to modify a signal (to suppress unwanted parts of the signal).

Filter characteristics:

• type (lowpass, highpass, bandpass, bandstop)
• cutoff frequency
• order (steepness)
• FIR, IIR

  Image 6: Graph of Gain over Angular frequency

  It can have either a Finite Impulse Response or FIR (the response of the filter after an impulse will reach exactly zero, after a certain, finite amount of time.) or an Infinite Impulse Response (IIR) if feedback is present in the topology of the filter.

A comparison between the continuous and discrete signal:

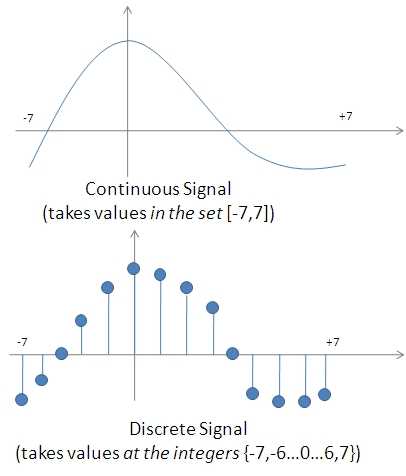Image 7:Comparison between the continuous and discrete signal

HTML Events

HTML Events
abort
afterprint
animationend
animationiteration
animationstart
beforeprint
beforeunload
blur
canplay
canplaythrough
change
click
contextmenu
copy
cut
dblclick
drag
dragend
dragenter
dragleave
dragover
dragstart
drop
durationchange
ended
error
focus
focusin
focusout
fullscreenchange
fullscreenerror
hashchange
input
invalid
keydown
keypress
keyup
load
loadeddata
loadedmetadata
loadstart
message
mousedown
mouseenter
mouseleave
mousemove
mouseover
mouseout
mouseup
offline
online
open
pagehide
pageshow
paste
pause
play
playing
progress
ratechange
resize
reset
scroll
search
seeked
seeking
select
show
stalled
submit
suspend
timeupdate
toggle
touchcancel
touchend
touchmove
touchstart
transitionend
unload
volumechange
waiting
wheel

HTML Event Objects
Animation Events
Clipboard Events
Drag Events
Events
Focus Events
HashChange Events
Input Events
Keyboard Events
Mouse Events
PageTransition Events
PopState Events
Progress Events
Storage Events
Touch Events
Transition Events
Ui Events
Wheel Events

HTML Event Properties
altKey (Mouse)
altKey (Key)
animationName
bubbles
button
buttons
cancelable
charCode
clientX
clientY
code
ctrlKey (Mouse)
ctrlKey (Key)
currentTarget
data
defaultPrevented
deltaX
deltaY
deltaZ
deltaMode
detail
elapsedTime
elapsedTime
eventPhase
inputType
isTrusted
key
keyCode
location
metaKey (Mouse)
metaKey (Key)
newURL
oldURL
offsetX
offsetY
pageX
pageY
persisted
propertyName
relatedTarget
relatedTarget
screenX
screenY
shiftKey (Mouse)
shiftKey (Key)
target
targetTouches
timeStamp
touches
type
which (Mouse)
which (Key)
view

HTML Event Methods
getModifierState()
preventDefault()
stopImmidiatePropagation()
stopPropagation()

How The Array Filter() Method Works

The array filter method creates a new array of elements based on elements of the original array that pass a logical condition or test function defined in a callback function. The array filter method concept might sound confusing when reading it for the first time, but it doesn’t have to be. To make things more clear, let’s look a the following image.

How Array Filter Method Works in JavaScript

As you see in the previous image, we have an array of geometrical shapes: there are triangles, squares, and circles with different colors. Let’s say we are only interested in getting triangles from that array. Hence, we use the filter method to define the conditions of those elements we want to keep inside. As a result, we get a list of elements filtered. Notice how a new array is created instead of replacing the original array.