Гениальные математические игры с калькулятором

Правила вычитания двоичных чисел

0-0=0
1-0=0
10-1=1

Но как быть с 0-1=? Вычитание двоичных чисел немного отличается от вычитания десятичных чисел. Для этого используется несколько способов.

Вычитание методом заимствования

Запишите двоичные числа друг под другом – меньшее число под большим. Если меньшее число имеет меньше цифр, выровняйте его по правому краю (так, как вы записываете десятичные числа при их вычитании).
Некоторые задачи на вычитание двоичных чисел ничем не отличаются от вычитания десятичных чисел. Запишите числа друг под другом и, начиная справа, найдите результат вычитания каждой пары чисел.

Вот несколько простых примеров:

1 — 0 = 1
11 — 10 = 1
1011 — 10 = 1001

Рассмотрим более сложную задачу. Вы должны запомнить только одно правило, чтобы решать задачи на вычитание двоичных чисел. Это правило описывает заимствование цифры слева, чтобы вы могли вычесть 1 из 0 (0 — 1).

110 — 101 = ?

В первом столбце справа вы получаете разность 0 — 1. Для ее вычисления необходимо позаимствовать цифру слева (из разряда десятков).

1010 — 101 = ?101100 — 101 = ?

101100 — 101 = ?

10 — 1 = 1102 = (1 x 2) + (0 x 1) = 210

12 = (1×1) = 110.

Таким образом, в десятичной системе эта разность записывается в виде: 2 — 1 = 1.

Вычтите цифры в оставшихся столбцах. Теперь это легко сделать (работайте со столбцами, двигаясь, справа налево):

101100 — 101 = __1 = _01 = 001 = 1.

Вычитание методом дополнения

Запишите двоичные числа друг под другом так, как вы записываете десятичные числа при их вычитании. Этот метод используется компьютерами для вычитания двоичных чисел, так как он основан на более эффективном алгоритме.

Однако простому человеку, привыкшему вычитать десятичные числа, этот метод может показаться более сложным (если вы программист, обязательно познакомьтесь с этим методом вычитания двоичных чисел).

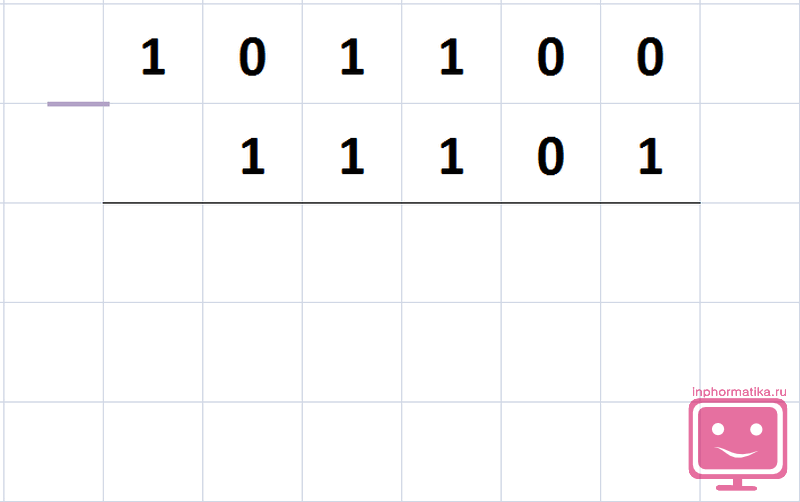
101100₂ — 11101₂= ?

Если значность чисел разная, к числу с меньшей значностью слева припишите соответствующее количество 0.

101100₂ — 011101₂= ?

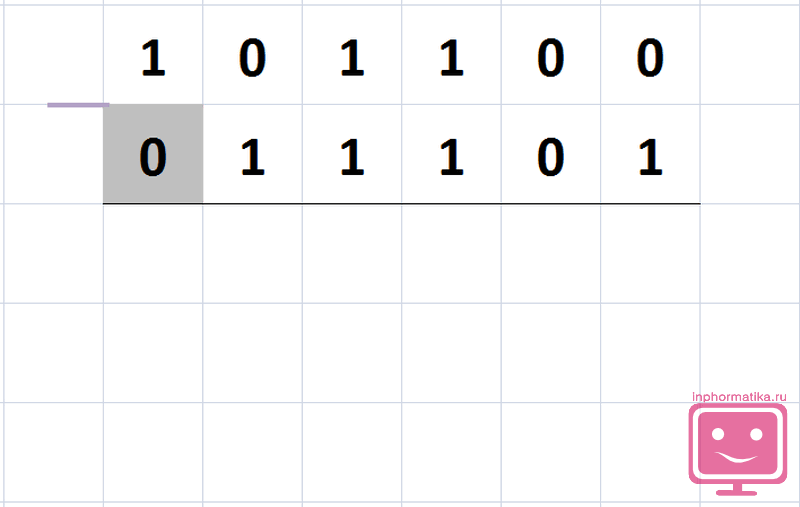
В вычитаемом числе поменяйте цифры: каждую 1 поменяйте на 0, а каждый 0 на 1.

011101₂ → 100010₂.

На самом деле мы «забираем дополнение у единицы», то есть вычитаем каждую цифру из 1. Это работает в двоичной системе, так как у такой «замены» может быть только два возможных результата: 1 — 0 = 1 и 1 — 1 = 0.

К полученному вычитаемому прибавьте единицу.

100010₂+ 1₂ = 100011₂

Теперь вместо вычитания сложите два двоичных числа.

101100₂ +100011₂= ?

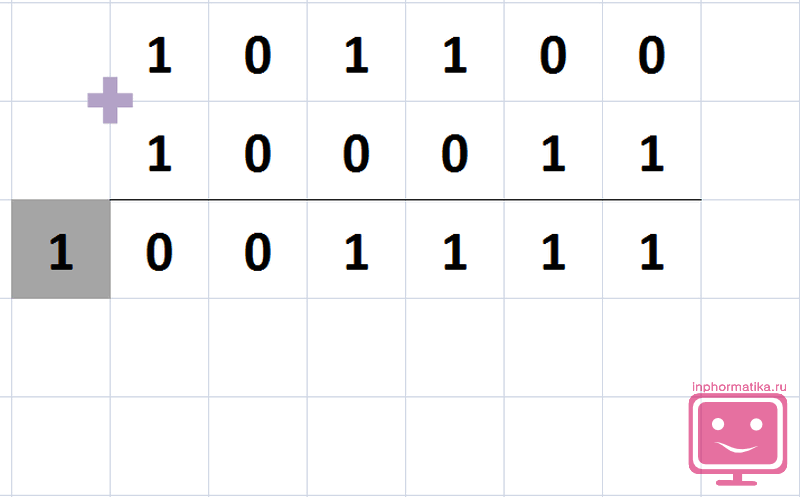
Проверьте ответ. Быстрый способ – откройте двоичный онлайн калькулятор и введите в него вашу задачу. Два других метода подразумевают проверку ответа вручную.

1) Переведем числа в двоичную систему счисления:
Допустим, что из числа 101101₂ нужно вычесть 11011₂

2) Обозначим как A число 101101₂ и как B число 11011₂.

3) Запишем числа A и B столбиком, одно под другим, начиная с младших разрядов (нумерация разрядов начинается с нуля).

Разр.	6	5	4	3	2	1
A		1	1	1	1
B			1	1	1	1

4) Вычтем разряд за разрядом из числа A число B записывая результат в C начиная с младших разрядов. Правила поразрядного вычитания, для двоичной системы счисления представлены в таблице ниже.

Заем из текущего разряда Oi-1	Ai	Bi	Ci	Заем из следующего разряда Oi+1
	1	1	1
	1	1
	1	1
1	1	1
1	1	1
1	1
1	1	1	1	1

Весь процесс сложения наших чисел выглядит следующим образом:

(красным шрифтом показаны заёмы из соответствующего разряда)

101101₂ — 11011₂ = 10010₂45₁₀ — 27₁₀ = 18₁₀

Игра начинается, партнер последовательно делит числа пополам

Предположим, наш товарищ по игре на своем калькуляторе набрал число 78. Мы этого не видим, и не знаем данное число. Тем не менее, оно теперь набрано на калькуляторе. Отлично! Мы же откроем обычный блокнот в компьютере или в любом другом устройстве (телефон, смартфон, айфон, планшет и прочее).

У кого нет блокнота – подойдет любой редактор, куда можно записывать символы. Да хоть обычный блокнот с карандашом или авторучкой – не обязательно на компьютере. Будем записывать только нули и единицы – ведь речь пойдет о двоичной системе счисления…

Вот как все это выглядит: на рисунке 1 показано, что слева – это наш блокнот, пока пустой, в нем ничего не записано. А справа – калькулятор нашего товарища, на котором он (она) уже успел(а) набрать загаданное число 78.

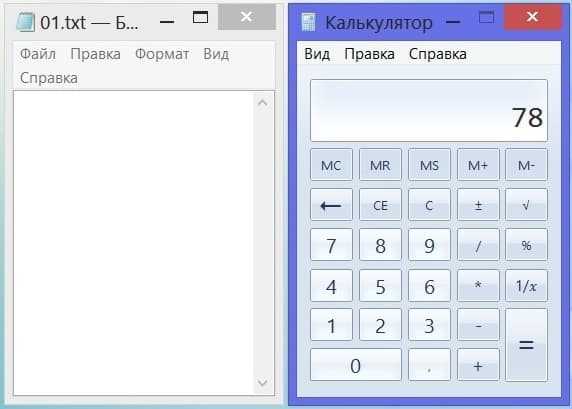
Рис. 1. Калькулятор одного игрока (справа) с загаданным числом 78 и блокнот второго игрока (слева) в игре «Угадай число».

Итак, поехали, игра «Угадай задуманное число» началась! Будем угадывать набранное число. Для начала попросим нашего товарища разделить загаданное число на 2. Это можно сделать прямо на том же калькуляторе.

Перед этим снова обратим внимание напарника на то, что он должен обязательно запомнить задуманное число! Поскольку оно сотрется с экрана калькулятора после производимых над ним арифметических действий

Как делить число на 2 на калькуляторе

Смотрим на рисунок 2. Сначала нажимаем на знак деления «/» (на некоторых калькуляторах используется другой символ). Потом нажимаем на кнопку с цифрой 2. И, наконец, жмем на знак равенства «=».

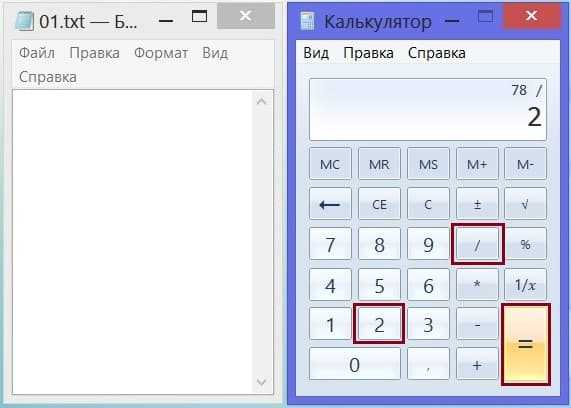
Рис. 2. Как делить число на 2 с помощью калькулятора: последовательное нажатие на кнопки «/» (делить), «2» и «=» (равно).

Результат деления задуманного числа видит наш товарищ, но мы этот результат не видим. Получилось число 39. Когда любое целое число делят на 2, может получиться либо целое число, либо дробное, у которого после точки (или запятой, как бывает на некоторых калькуляторах) будет стоять «пятерка» — пять десятых. Других вариантов деления на 2 не бывает.

Вот и мы обратим на это внимание. Попросим нашего товарища нам сообщить, какое число он получил в результате деления на 2 – целое или дробное. Он нам должен сказать не само число, которое получилось, а именно целое оно или дробное, с «пятеркой» после десятичной точки

Он нам должен сказать не само число, которое получилось, а именно целое оно или дробное, с «пятеркой» после десятичной точки.

Как мы уже отметили, ответ получился целым – число 39. Нам сообщают, что число целое. У нас перед глазами находится блокнот. И мы в него записываем либо «единичку» (1), либо «нолик» (0):

• 1 – единицу пишем в том случае, если ответ получился дробный, с точкой и с «пятеркой» после точки
• 0 – нолик пишем тогда, когда ответ получается целый без десятичной точки.

Нам сказано, что результатом деления задуманного числа на 2 есть целое число, без десятичной точки. Значит, записываем в блокнотик одну единственную цифру «нолик» — 0 (рис. 3).

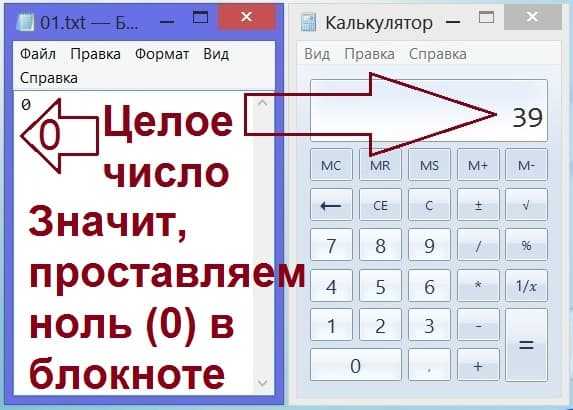
Рис. 3. Запись в блокнот (слева) первого игрока цифры «ноль» (0), если на калькуляторе (справа) второго игрока получилось целое число без десятичной точки.

Хакерский редактор Hacker Viewer (Hiew) .

Для визуального восприятия шестнадцатеричного кода воспользуемся замечательным простым, но достаточно функциональным DOS редактором Hacker Viewer (Hiew). Вы найдёте его в папке D:\UTILS\HIEW\ (я надеюсь, что наш архив программ DOS-1.rar уже скачан и DOSBox установлен и запущен).

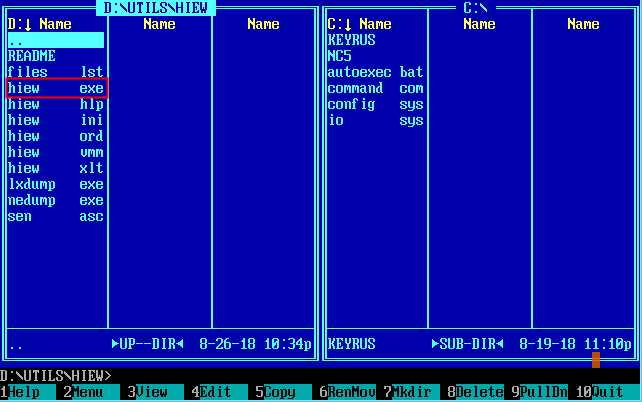Запускаем HIEW (Hacker Viewer).

Инструкцию по пользованию Hiew для хакеров от Криса Касперского вы найдёте в папочке readme. Пользоваться редактором просто и удобно.

Откроем с помощью Hiew нашу программу PRG.COM (выбор файлов — F9). При помощи F4 выбираем режим отображения информации HEX (как вы уже знаете, шестнадцатеричный режим). Можете с помощью F4 или Enter по переключаться между режимами отображения.

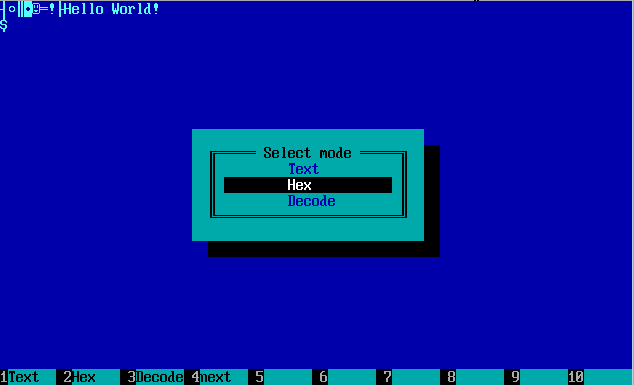Переключение режимов отображения в Hacker Viewer.

Обратите внимание на положение Decode (декодирование). Вам это ни о чём не говорит? Да, да, да в Hiew имеется встроенный дизассемблер и даже ассемблер! Можно внести изменения в ассемблерный код, не выходя из редактора и сохранить изменения.
Исполняемый файл останется рабочим — гениальная программа с поразительными возможностями для своего времени!. Подобное отображение HEX системы счисления вы увидите практически во всех отладочных программах и просмотрщиках файлов.
Перемещайте курсор с помощью клавиш стрелок на клавиатуре

Вверху вы заметите изменение цифры указателя (pointer)

Подобное отображение HEX системы счисления вы увидите практически во всех отладочных программах и просмотрщиках файлов.
Перемещайте курсор с помощью клавиш стрелок на клавиатуре. Вверху вы заметите изменение цифры указателя (pointer).

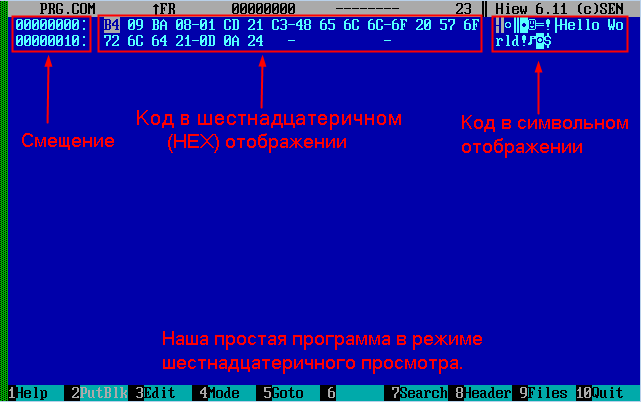Наша первая программа в шестнадцатеричном виде.

Указатель является одним из основополагающих понятий в системе программирования. Основы понимания работы с указателем рассмотрим попозже.

Скрываем элементы

Чтобы скрыть то, что сейчас на экране, мы сделаем так:

1. В том же проекте с калькулятором возьмём код, который добавляет и убирает классы у разных элементов на странице.
2. Добавим класс скрытия текущим элементам.

Первый пункт делается просто — добавим в стили такой блок:

А чтобы скрыть элементы, в стартовой функции напишем две команды:

// скрываем приветственную надпись и кнопку document.getElementById(«startText»).classList.add(«notOnScreen»); document.getElementById(«startButton»).classList.add(«notOnScreen»);

Всё, теперь при нажатии на кнопку у нас снова будет пустая страница.

О возможной пользе троичной, четверичной и иных систем счисления

Кстати, аналогично можно преобразовать десятичное число в троичное. Только придется делить нацело не на 2, а на 3. Тоже потребуется записывать цифры из остатка, которые могут быть 0, 1 и 2. Для перевода в четверичную систему делить уже придется на 4, а в остатке записывать цифры 0, 1, 2, 3. И так далее – для любой системы исчисления правила однотипные, только делить приходится на разные числа.

А как потом преобразовать троичное или четверичное число в десятичное? На какие множители придется умножать цифры 0, 1, 2 и 0, 1, 2 и 3 соответственно? Как Вы думаете?! Делаем паузу, чтобы можно было подумать самостоятельно…

• …В двоичной системе – то были цифры 1, 2, 4, 8 и так далее – каждое последующее число есть предыдущее, умноженное на 2.
• А в троичной же системе это будут цифры 1, 3, 9, 27 и так далее – каждое последующее число есть умножение на 3.
• В четверичной системе: 1, 4, 16, 64 и так далее – теперь умножаем каждое число на 4!

Можете теперь самостоятельно записать аналогичные числа в пятеричной системе?! А в шестеричной?..

Вот так, довольно просто и единообразно можно преобразовывать числа из десятичной системы счисления в любые другие системы. Зачем? Например, показывать фокусы!

О системах счисления в технике

В технике тоже нужны иные системы счисления. Допустим, по проводу может протекать ток. Если по нему либо есть ток, либо нет – это двоичная система. А если по проводу ток может течь в два направления «+» и «-», то тут мы имеем дело с троичной системой: «-» (ток течет в обратном направлении), «0» (нет тока), «+» (ток течет в прямом направлении). Придется рассчитывать подобные цепи с применением троичной системы исчисления.

Или, скажем, если нам придется пользоваться старинными весами с двумя чашками, куда и слева, и справа можно ставить разные гирьки. Тогда, как оказывается, самые универсальные разновесы с наименьшим числом гирек получаются, если они будут сделаны не в привычной двоичной системе (1, 2, 4, 8 и так далее), а в троичной системе (1, 3, 9, 27 и так далее).

Но эти гирьки 1, 3, 9, 27, или ток, текущий в разных направлениях, что называется, уже совсем другая история…

Другие материалы:

1. Кодирование текстовой информации

2. Домик в системном блоке

3. Сказка про мудрого правителя Процессора, про злого Вируса и неутомимого Анти Вируса

4. Игра Крестики-нолики онлайн в Google и в браузере Google Chrome

Распечатать статью

Получайте актуальные статьи по компьютерной грамотности прямо на ваш почтовый ящик. Уже более 3.000 подписчиков

Важно: необходимо подтвердить свою подписку! В своей почте откройте письмо для активации и кликните по указанной там ссылке. Если письма нет, проверьте папку Спам

Математические фокусы. Начальная школа

1. Угадывание номера дома.

Учитель рисует на доске 10 домиков с номерами. Дети загадывают номер одного из домов. Учитель предлагает из задуманного номера дома вычесть 1, прибавить 1, и еще 1, и еще 1. Дети поочередно называют ответы, учитель отгадывает, какой номер дома загадал ученик. Для этого он вычитает из результата число 2. Можно спросить детей, в чем секрет этого фокуса.

2. Угадывание месяца рождения.

Порядковый номер месяца рождения увеличьте на 6, уменьшите на 5. Назовите результат.

Для отгадывания надо из названного учеником результата вычесть единицу, получится месяц его рождения.

3. Угадывание числа палочек.

На столе лежат 10 палочек. Учитель предлагает ученику взять большую часть палочек в правую руку, остальные в левую. После этого переложить из правой руки в левую столько палочек, сколько в левой было, и вслух назвать число палочек, оставшихся в правой руке.

Учитель отгадывает, сколько палочек было взято в каждую руку первоначально. Для этого ему достаточно из 10 вычесть названное вслух число и полученный ответ разделить на 2. Получив таким подсчетом число палочек, взятых в левую руку, легко определить, сколько их было в правой руке. Для этого надо из 10 вычесть число палочек, полученных при делении на 2.

4. Угадывание количества членов семьи.

К числу членов семьи прибавить 1, полученное число умножить на 2, от последнего результата отнять 3.

Чтобы угадать число членов семьи ученика (а одно и то же число получится одновременно у нескольких учащихся), учитель к названному последнему числу прибавляет единицу и делит это число на 2.

Учитель может через некоторое время раскрыть секрет и попросить детей самостоятельно угадать задуманные ими числа.

5. Угадывание задуманного числа.

На доске нарисован круг с числами.

— Задумай число, при каждом стуке указкой прибавляй к нему по 1, пока не получится 20. Вместо 20 скажи вслух «стоп». Указка в это время укажет на задуманное число.

Для того чтобы так получилось, отгадывающему можно 7 раз указать на любые числа, восьмым числом должно быть указано число 12, затем указка идет последовательно от числа к числу против движения часовой стрелки, указывая числа 11, 10, 9, 8, …, 1.

6. Угадывание месяца в году.

— Задумай любой месяц. Вспомни его порядковый номер и произведи с этим числом следующие действия: прибавь к нему 17, вычти 18, прибавь 27, вычти 23. Назови результат.

По результату можно угадать задуманный месяц в году. Например, задуман сентябрь — это девятый месяц по порядку. С числом 9 производятся следующие действия:

1) 9 + 17 = 26;                    3) 8 + 27 = 35;

2) 26 — 18 = 8;                     4) 35 — 23 = 12.

Для отгадывания надо из результата вычесть число 3 и вспомнить название месяца.

7. Угадывание чисел.

— Напиши двузначное число, в котором цифра десятков больше или меньше цифры единиц на 2 или более. Переставь в этом числе цифры. Из большего числа вычти меньшее. В полученном числе снова переставь цифры. Это число сложи с полученной ранее разностью. В результате получится 99.

Для большего эффекта это число можно заранее написать, положить в конверт и дать одному из учеников.

Очень простая математическая задачка-фокус быстро угадает ваш возраст

Социолог, психолог, специалист по массовой коммуникации, редактор

Время на чтение: 1 минута

Этот интересный математический трюк может вас позабавить. Как? Дело в том, что он обещает угадать не только выбранное вами число, но и ваш точный возраст.

Проверьте сначала его на себе, а потом выдайте другу калькулятор (или бумагу и ручку) и попросите выполнить ту же последовательность действий.

Внимательно следуйте приведённым инструкциям и приготовьтесь удивиться! Кстати, а вы можете определить, в чём же заключается фокус?

Инструкция

Получили ли вы правильный ответ? Если нет, убедитесь, что вы правильно всё подсчитали. Попробуйте этот математический трюк на своих друзьях и домочадцах!

Психолог, эксперт журнала Colady. Специалист по массовой коммуникации и межличностным отношениям. Редактор.

Как преобразовать двоичное число в десятичное

Нам же осталось только преобразовать двоичное число в десятичное, как только мы узнали, что задуманное число есть 1001110. Это было сделано с помощью калькулятора для программиста – ввод двоичного числа с получением взамен десятичного.

А можно ли «вручную» преобразовать двоичное число в десятичное? Конечно. Для этого нужно каждую единичку умножить на соответствующий разряд  этого двоичного числа. А потом все цифры сложить. Если не ошибиться при работе «руками», то результат непременно получится 78.

На рисунке 17 продемонстрировано, как мы в игровой форме преобразовывали десятичное число сначала в двоичное, а потом наоборот. Каждое деление нацело на 2 давало нам в остатке 0 или 1. Из этих «нулей» и «единиц» мы формировали и записали двоичное число 1001110. А затем произвели обратное преобразование в десятичный вид путем умножения с последующим сложением:

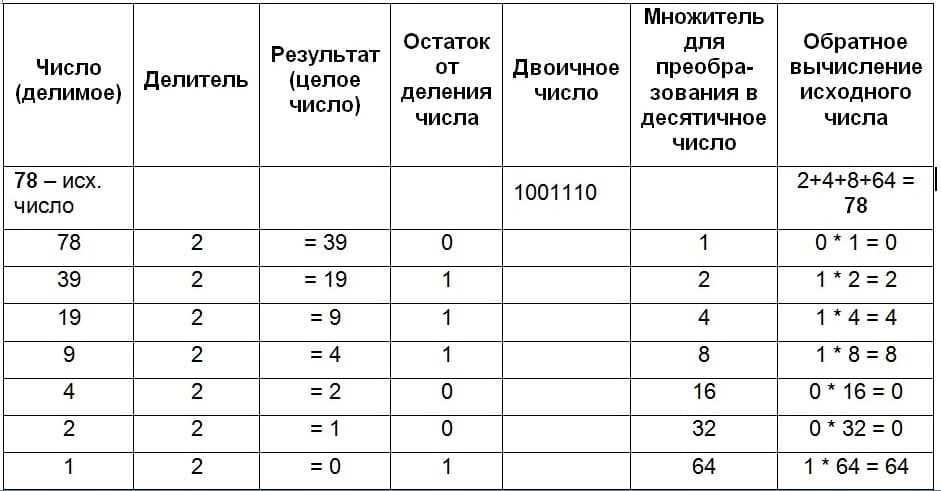
Рис 17 (Кликните для увеличения). Таблица, демонстрирующая вычисления для преобразования задуманного десятичного числа в двоичное, и затем – наоборот.

Приведенный рисунок наглядно показывает нам, как преобразуется десятичное число в двоичное: путем последовательного деления на 2. Наоборот, двоичное число превращается в десятичное число с помощью умножения каждого нолика и единички на такие числа, как 1, 2, 4, 8, 16, 32, 64, 128, … После чего все числа складывают и получают требуемый результат.

Вот так можно использовать наши знания двоичной системы исчисления для небольшого приятного фокуса «Угадай число!».

Глава 4. Пишем игру «Угадай число» на Python.

В этой главе мы напишем игру «Угадай число» на Python. Помните, как в мультфильме «Алеша Попович и Тугарин змей», конь Юлий играл с деревом? Здесь будет примерно такой же алгоритм: компьютер будет загадывать число от 1 до 20. Ваша задача угадать число, которое задумал компьютер за 6 попыток. После каждой неудачной попытки, компьютер будет давать подсказку: задуманное число больше или меньше вашего ответа.

Эта игра является хорошей практикой по языку Python — в этой небольшой программе м иты будем использовать все ранее изученные функции, кроме того, рассмотрим несколько новых.Вы узнаете, как преобразовывать различные типы данных и зачем это нужно. Так как у нас игровая программа, то мы будем называть пользователя «Игрок», хотя «Пользователь» тоже является правильным определением.

Пример работы программы «Угадай число».

Ниже представлен примерный вид того, как будет выглядеть окно интерпретатора Python после запуска и выполнения программы «Угадай число»(guessesTaken.py). Данные, которые вводит игрок выделены черным цветом:

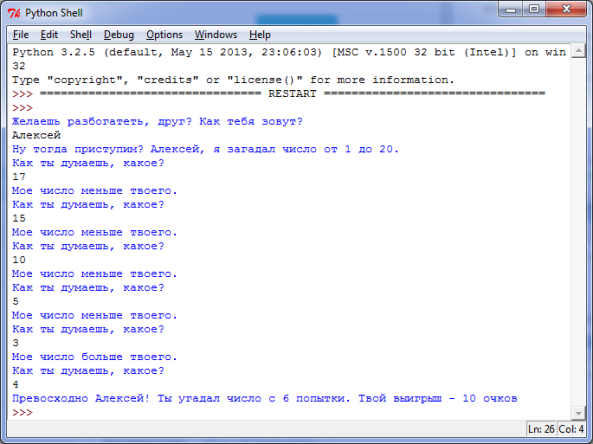
Рисунок 4-1. Работа программы «Угадай число». Данные, вводимые игроком, выделены черным цветом.

Исходный код программы «Угадай число».

Откройте окно редактора файлов IDLE, нажав меню «File»->»New Window». В открывшемся окне, внимательно перепечатайте приведенный ниже код. Сохраните файл с именем guess.py, после чего запустите выполнение программы нажатием кнопки «F5»

Обратите внимание, что в начале некоторых строк необходимо добавить 4 или 8 пробелов. Вообще-то, редактор сам это сделает

Просто имейте ввиду, что это не ошибка, а так и должно быть.

Важно! В очередной раз напоминаю, что данный код предназначен для версии Python 3.0 и выше. В версии Python 2.x эта программа работать не будет

Скачать необходимую версию Python можно с моего сайта (страница «Загрузки) или с официального сайта http://www.python.org.

1. # Это программа «Угадай число»
2. import random
3. guessesTaken = 0
4. print ( ‘Желаешь разбогатеть, друг? Как тебя зовут?’ )
5. myName = input ()
6. number = random.randint(1,20)
7. print ( ‘Ну тогда приступим? ‘+myName+’, я загадал число от одного до 20′ )
8. while guessesTaken < 6:
9. print ( ‘Как ты думаешь, какое?’ ) #Перед функцией print() должно быть 4 пробела
10. guess = input ()
11. guess = int (guess)
12. guessesTaken = guessesTaken+1
13. if guess < number:
14. print ( ‘Мое число больше твоего’ ) #Перед функцией print() должно быть 8 пробелов
15. if guess > number:
16. print ( ‘Мое число меньше твоего’ )
17. if guess == number:
18. break
19. if guess == number:
20. guessesTaken = str (guessesTaken)
21. print ( ‘Превосходно ‘ +myName+ ‘! Ты угадал число с ‘ +guessesTaken+ ‘ попытки. Твой выигрыш 10 очков.’ )
22. if guess != number:
23. number = str (number)
24. print ( ‘Жаль, но у тебя не осталось попыток. Я загадал число ‘ +number+ ‘. Ты проиграл… Эй! Вы! Двое! Живо! Снимите ка с него шкуру!’ )

Хотя я настоятельно рекомендую перепечатывать код программы вручную, вы можете просто скопировать его отсюда, или скачать файл с готовой программой на странице «Загрузки«.

https://amdy.su/wp-admin/options-general.php?page=ad-inserter.php#tab-8

Последние заданные вопросы в категории Информатика

Информатика 06.09.2023 23:11 27 Белов Юра.

Часть 3 Составить блок-схемы программ, напишите их на отдельном листе: (3 балла) Составить блок-сх

Ответов: 1

Информатика 06.09.2023 23:07 14 Ефанова Настя.

Диаграмма, у которой для каждой точки ряда данных предусмотрена своя ось

Ответов: 1

Информатика 06.09.2023 23:06 14 Никифорова Настя.

Составить программу,которая: а)из слов «программа»составляет слова: » грамм», «рога», «гора»; б) и

Ответов: 1

Информатика 06.09.2023 23:03 15 Линберг Давид.

Ввести одномерный массив размерностью n. Вывести значение и номер последнего четного элемента или со

Ответов: 1

Информатика 06.09.2023 22:27 13 Епифанцева Алиса.

для хранения растрового изображения размером 56х64 пикселя отвели 1,75 килобайта памяти. Каково макс

Ответов: 1

Информатика 06.09.2023 22:25 29 Кучаева Настя.

Контрольная работа считается лёгкой, если за любой партой сидит ученик, решивший её наполовину, и не

Ответов: 2

Информатика 06.09.2023 22:25 5 Мироненко Софья.

18) Для групповых операций с файлами используются маски имен файлов. Маска представляет собой посл

Ответов: 1

Информатика 06.09.2023 22:24 25 Поздняков Никита.

Составить подпрограмму,заменяющую все элементы одномерного массива,меньшие заданной величины Т,на зн

Ответов: 1

Информатика 06.09.2023 22:22 17 Чернышов Александр.

Как нарисовать часы для информатики 5 класс

Ответов: 1

Информатика 06.09.2023 22:22 25 Алиева Злата.

Системы счисления : 100111 в (2) — перевести в 4,8,10,16 301 в (4) -2,8,10,16 706 в (8) — 2,4,10,1

Ответов: 1

Двоичная (бинарная) система счисления

Двоичная (или бинарная) система счисления — это позиционная система счисления с основанием 2.

Принцип считать двумя цифрами берёт своё начало ещё в Древнем Китае. Но развитие современной бинарной системы началось в XVII веке, а применение нашлось только в середине XX века.

История двоичной системы счисления

В 1605 году английский астроном и математик Томас Хэрриот описал двоичное представление чисел, а философ Фрэнсис Бэкон создал шифр из двух символов — A и B.

В 1670 году испанский богослужитель Хуан Карамюэль-и-Лобковиц опубликовал представление чисел в разных системах счисления, в том числе и двоичной.

Но самым значительным событием стали работы немецкого математика Готфрида Лейбница, который в 1703 году описал двоичную арифметику — математические операции с двоичными числами.

В 1838 году американский изобретатель Сэмюэл Морзе создал одноимённый шифр, содержащий два символа: «точка» и «тире». Их можно было передавать по телеграфу в виде длинных и коротких сигналов. Азбука Морзе не была бинарной системой в строгом смысле слова, но двоичный принцип впервые показал свою значимость.

В 1847 английский математик Джордж Буль изобрёл «булеву алгебру», в которой было два понятия («ложь» и «истина»), а также ряд логических законов.

В 1937 году американский инженер Клод Шеннон объединил бинарный принцип, булеву логику и электрические схемы и ввёл понятие «бит» — минимальное количество информации:

•  — ложь — нет тока (0 бит);
• 1 — истина — есть ток (1 бит).

С тех пор двоичную (бинарную) систему счисления стали использовать все ЭВМ, в том числе и современные компьютеры.

Числа в двоичной системе счисления

Двоичное число — это число, состоящее из двоичных цифр. А у нас их всего две. Принято обозначать и 1, но, как показала практика, это могут быть и два разных значения: «лампа горит» и «лампа не горит», «ток» и «нет тока» и так далее.

В следующей таблице приведены числа в двоичной системе (зелёный столбец) и соответствующие им числа в других часто используемых системах счисления — восьмеричной, десятичной и шестнадцатеричной.

Изображение: Лев Сергеев для Skillbox Media

Преимущества и недостатки двоичной (бинарной) системы счисления

Явные минусы двоичной системы обусловлены тем, что на интуитивном уровне людям она чужда — в отличие, например, от десятичной. И это — первый недостаток. Пройдёмся по остальным:

Длинная запись, неудобство с большими числами. Возьмём, к примеру, обозначение белого цвета в RGB-палитре: 25510, 25510, 25510 (здесь и далее нижний индекс указывает основание системы — двоичная, десятичная и так далее). Значения цветов принято записывать в шестнадцатеричной системе счисления (FF16, FF16, FF16). Если перевести это в бинарный вид, получится громоздко и непонятно:

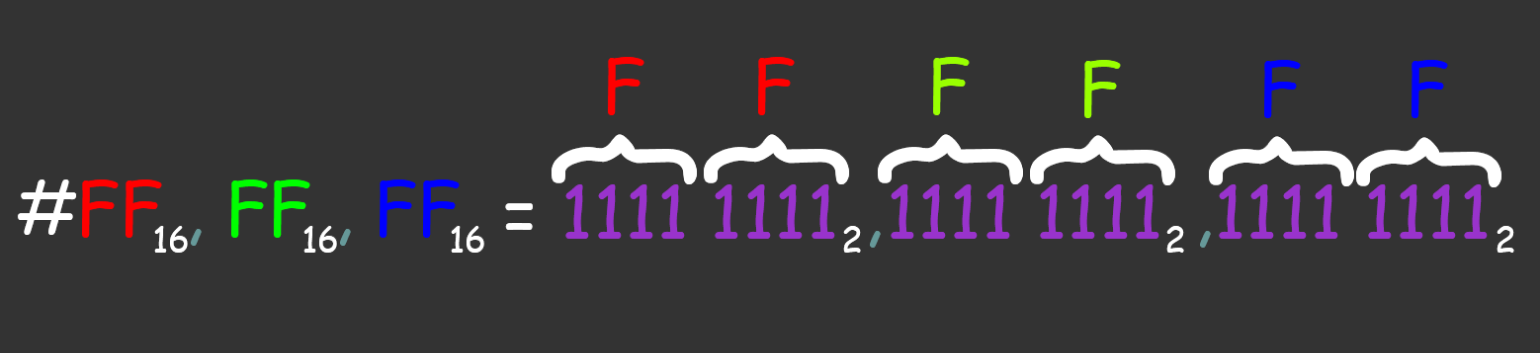
Изображение: Лев Сергеев для Skillbox Media

• Долгое время ручных вычислений.
• Не применяется в повседневной жизни (если, конечно, вы не компьютер).

А вот для ЭВМ бинарочка — как родная. И отсюда следуют её плюсы:

• Позиционная система, имеет разряды.
• Применимы арифметические действия.
• Можно построить логику.
• Подходит для шифровки данных.
• Родной язык компьютерных систем.

Угадываем день рождения

Объявите участников математического фокуса, что вы можете угадать дату дня рождения любого из них.

Пусть доброволец умножит на 2 число дня своего рождения.

К получившемуся числу надо прибавить 5.

Результат надо умножить на 50.

Теперь к получившемуся числу прибавляют месяц рождения и назвать результат вслух.

Ведущий мысленно отнимает от названного числа число 250. Получается трехзначное или четырехзначное число. Первая и вторая цифры — день рождения, две последние — месяц.

Всё это укладывается в ряд формул:

1. x*2
2. x*2+5
3. (x*2+5)*50
4. (x*2+5)*50+y=z
5. z-250=(x*2+5)*50+y-250=x*100+250+y-250=X*100+y=w

• ЕГЭ-Математика. Узнай свой результат!
• «Вычисляю квадратный корень, покрываясь холодным потом». Почему мы боимся математики

Поскольку вы здесь…

У нас есть небольшая просьба. Эту историю удалось рассказать благодаря поддержке читателей. Даже самое небольшое ежемесячное пожертвование помогает работать редакции и создавать важные материалы для людей.

Сейчас ваша помощь нужна как никогда.

ПОМОЧЬ

Обрабатываем нажатия на кнопки

Задача кнопок «Больше» и «Меньше» — сократить пополам диапазон возможных значений. Для этого они делят его пополам и округляют до целого числа. Проблема в том, что иногда компьютер может округлить число обратно до минимальной или максимальной границы и предложить это же число заново.

Чтобы такого не было, добавим в функции простую проверку: если новая граница совпадает с минимальным или максимальным значением диапазона, то принудительно двигаем её на единицу в нужную сторону.

Финальный штрих: добавим в каждую функцию в конце проверку на выигрыш. Так как проверка везде одинаковая, то сделаем её отдельной функцией.

Ограничения и ошибки в работе [ править | править код ]

На текущий момент во всех версиях Windows, включая 64-разрядные, калькулятор имеет ограничение при выполнении операции возведения числа в целую степень. Данное ограничение, связанное с переполнением, возникает при возведении в целую степень, если показатель степени нельзя представить 32-разрядным целым числом. В этом случае выдаётся сообщение «Недопустимый ввод». В то же время использование приблизительно такого же, но дробного показателя степени не приводит к ошибке. Пусть, например, нужно вычислить 0.999999999 − 3000000000 <displaystyle 0.999999999^<-3000000000>> . Непосредственное вычисление выражения приводит к ошибке, однако, например, выражение 0.999999999 − 3000000000.5 <displaystyle 0.999999999^<-3000000000.5>> корректно вычисляется и даёт результат 20.085536963358741652581860232205 <displaystyle 20.085536963358741652581860232205> . Из него можно получить:

0.999999999 − 3000000000 = 0.999999999 − 3000000000.5 ⋅ 0.999999999 = 20.085536953315973168391797284239 <displaystyle 0.999999999^<-3000000000>=0.999999999^<-3000000000.5>cdot <sqrt <0.999999999>>=20.085536953315973168391797284239>

Указанное выше ограничение при возведении в степень приводит к появлению бага (его уже вряд ли можно назвать ограничением). Он заключается в том, что при взятии противоположной величины от 32-разрядного целого числа − 2 31 = − 2147483648 <displaystyle -2^<31>=-2147483648> происходит переполнение, которое корректно не обрабатывается и приводит к аварийному завершению работы программы. Например, сбой может происходить при вычислении выражения

0.999999999 − 2147483648 <displaystyle 0.999999999^<-2147483648>> .

Правильный результат 8.5632830377708104878252734036038 <displaystyle 8.5632830377708104878252734036038> можно получить, изменив показатель степени, например следующим образом:

0.999999999 − 2147483648 = ( 0.999999999 2 ) − 1073741824 <displaystyle 0.999999999^<-2147483648>=(0.999999999^<2>)^<-1073741824>>

0.999999999 − 2147483648 = 0.999999999 − 2147483647 / 0.999999999 <displaystyle 0.999999999^<-2147483648>=0.999999999^<-2147483647>/0.999999999> .

Ещё ряд ограничений связан с непродуманной реализацией вычислительных алгоритмов, в результате чего для некоторых значений происходит потеря точности, иногда приводящая к существенным ошибкам. Так, стандартная формула вычисления ареа-синуса при больших по модулю отрицательных значениях аргумента приводит к вычитанию близких чисел и, как следствие, потере значащих цифр результата. Вычислим, например, с помощью калькулятора Windows ареа-синус ( sinh − 1 <displaystyle operatorname ^<-1>> ) от числа − 3 , 5 e + 100 <displaystyle -3,5e+100> . Получаем результат 149 , 01606898593917039273345339555 <displaystyle 149,01606898593917039273345339555> , не имеющий ничего общего с правильным ответом − 232 , 20441944845988170690449821188 <displaystyle -232,20441944845988170690449821188> . В данном случае правильный ответ можно получить, пользуясь свойством нечётности функции: arsh ⁡ x = − arsh ⁡ ( − x ) <displaystyle operatorname x=-operatorname(-x)> .

Для гиперболического тангенса ( tanh <displaystyle operatorname > ) некоторые значения аргумента признаются недействительными, хотя на самом деле функция существует и не вызывает переполнение для любых значений аргумента. А именно, при 10000>»> x > 10000 <displaystyle x>10000> 10000>»/> или x − 1000 <displaystyle x выдаётся сообщение «Недопустимый ввод». Данное ограничение является необоснованным, так как значения функции для указанных значений аргумента примерно равны 1 <displaystyle 1> и − 1 <displaystyle -1> соответственно.