Пирамида — свойства, признаки и формулы

Свойства правильной пирамиды

У такой фигуры можно отметить особые свойства.

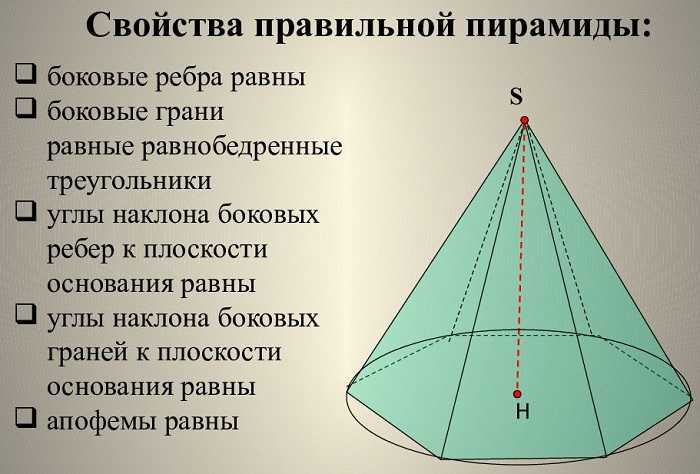
У правильной пирамиды все боковые треугольники одинаковы.

Каждая из них является равнобедренным треугольником.

Внутрь любой такого типа пирамиды можно вписать сферу. При этом она будет касаться основания и всех граней, имея с каждой из этих сторон по одной общей точке.

Снаружи возможна сфера, касающаяся всех вершин.

Нетрудно вычислить площадь поверхности такой фигуры. Для этого надо умножить длину периметра многоугольника, находящегося в её основании, на половину длины апофемы.

Особым случаем является ситуация, когда у вписанной и описанной сфер центры совпадают. В этом случае можно утверждать, что если сложить все плоские углы у боковых граней, то их сумма будет равна числу «Пи». При этом, для того чтобы узнать величину каждого из них, достаточно эту величину разделить на количество граней.

Некоторые свойства пирамиды

1) Если все боковые ребра равны, то

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Верно и обратное.

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр

Верно и обратное.

Элементы пирамиды

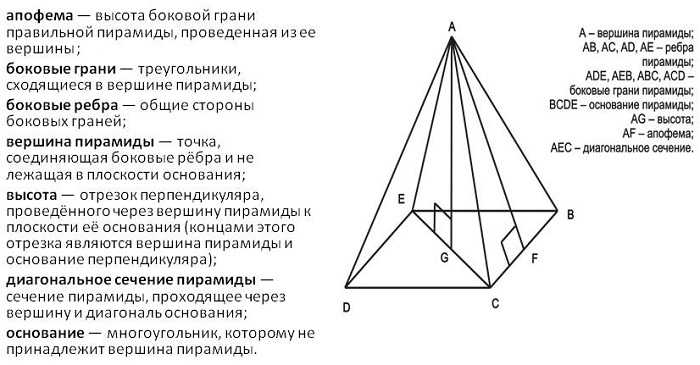
Элементами этой геометрической фигуры являются:

Место, куда сходятся все боковые грани фигуры, является вершиной.

Многоугольник, от каждой стороны которого отходят треугольные грани, носит название основания. Например, оно может быть шестиугольным.

Треугольники, соединяющиеся у вершины, с общей стороной с основанием, носят название боковых граней. У них противоположная вершина совпадает с точкой вершины пирамиды.

Высота фигуры представляет собой вертикальный отрезок, ограниченный многоугольником основания и вершиной.

На каждом треугольнике боковой стороны можно указать апофему. Она опускается от вершины по грани до ребра основания, будучи к нему перпендикулярной.

Боковыми ребрами называют те отрезки, которые соединяют соседние боковые грани.

У пирамиды может быть несколько диагональных сечений. Они включают в себя диагональ многоугольника вместе с вершиной пирамиды.

Связь пирамиды с цилиндром

Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одном основании цилиндра, а основание пирамиды вписано в другое основание цилиндра.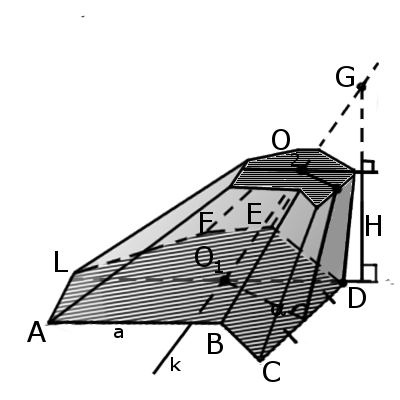
Определение Усеченная пирамида (пирамидальная призма) – это многогранник, который расположен между основанием пирамиды и плоскостью сечения, параллельной основанию. Таким образом, пирамида имеет большее основание и меньшее основание, подобное большему. Боковые грани представляют собой трапеции.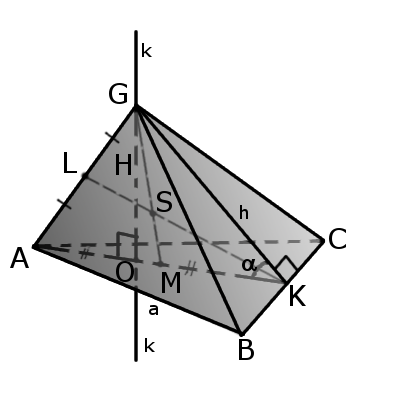
Определение. Тетраэдр имеет четыре грани, четыре вершины и шесть ребер, причем любые два ребра не имеют общих вершин, но не касаются друг друга. Каждая вершина состоит из трех граней и ребер, образующих треугольный угол. ГМ). Бимедиана называется отрезок, соединяющий середины противоположных ребер, не соприкасающихся (KL). При этом бимедианы делятся пополам, а медианы делятся в отношении 3:1 начиная с вершин.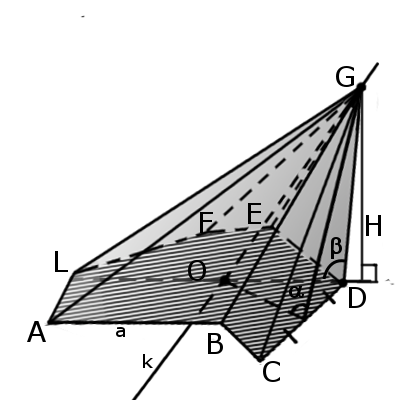
Опередение.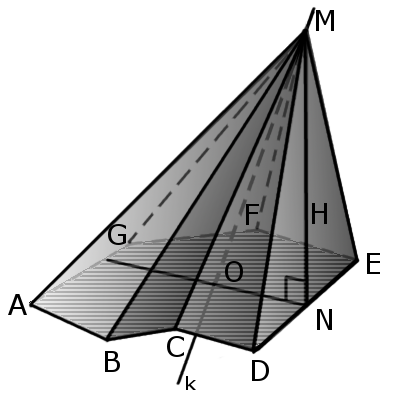
Определение.Прямоугольная пирамида — это пирамида, у которой одна из боковых граней перпендикулярна основанию. Это один из пяти правильных многоугольников. В правильном тетраэдре все двусторонние углы (между ребрами) и трехгранные углы (при вершине) равны. Три грани образуют прямоугольный трехсторонний угол, а грани — прямоугольные треугольники, а основание — произвольный треугольник. Апофема любого зерна равна половине стороны основания, на которое падает апофема. В таком тетраэдре грани являются равносторонними треугольниками.Определение.Ортоцентрическим тетраэдром называется четырехгранник, у которого все высоты (перпендикуляры), опущенные от вершины к противоположной грани, пересекаются в одной точке.Определение.Звездчатой ​​пирамидой называется многогранная пирамида, в основе которой лежит звезда.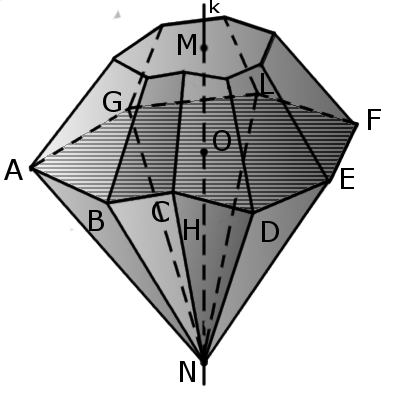
Определение Бипирамида — многогранная, состоящая из двух разных пирамид (также можно разрезать пирамиды), имеющих общее основание, причем вершины лежат по разные стороны от плоскости основания.

Сечения многогранника

В любом многограннике различают несколько видов сечения плоскостью. Зачастую в школьном курсе геометрии работают с двумя:

• осевое,
• параллельное основе.

Осевое сечение получают при пересечении плоскостью многогранника, которая проходит через вершину, боковые рёбра и ось. В данном случае осью является высота, проведённая из вершины. Секущая плоскость ограничивается линиями пересечения со всеми гранями, в результате получаем треугольник.

Внимание! В правильной пирамиде осевым сечением является равнобедренный треугольник. Если секущая плоскость проходит параллельно основанию, то в результате получаем второй вариант

В этом случае имеем в разрезе фигуру, подобную основе

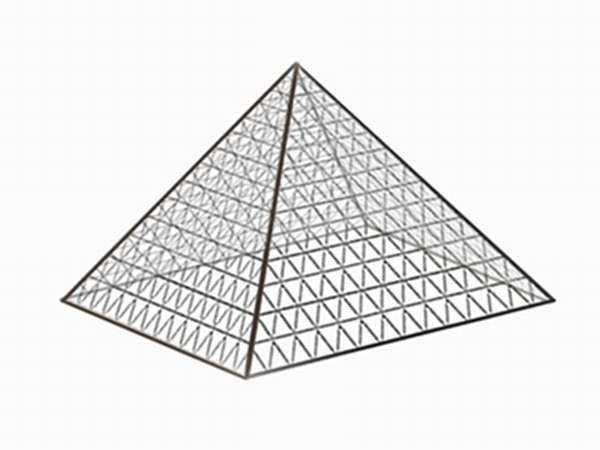Если секущая плоскость проходит параллельно основанию, то в результате получаем второй вариант. В этом случае имеем в разрезе фигуру, подобную основе.

К примеру, если в основании лежит квадрат, то сечение параллельно основе также будет квадратом, только меньших размеров.

При решении задач при таком условии используют признаки и свойства подобия фигур, основанные на теореме Фалеса. В первую очередь необходимо определить коэффициент подобия.

Если плоскость проведена параллельно основе, и она отсекает верхнюю часть многогранника, то в нижней части получают правильную усеченную пирамиду. Тогда говорят, что основы усеченного многогранника являются подобными многоугольниками. В этом случае боковые грани являются равнобокими трапециями. Осевым сечением также является равнобокая трапеция.

Для того чтобы определить высоту усеченного многогранника, необходимо провести высоту в осевом сечении, то есть в трапеции.

Основные свойства

Правильная пирамида обладает множеством свойств, которые присущи только ей. Перечислим их:

1. Основа – фигура правильной формы.
2. Ребра пирамиды, ограничивающие боковые элементы, имеют равные числовые значения.
3. Боковые элементы – равнобедренные треугольники.
4. Основание высоты фигуры попадает в центр многоугольника, при этом он одновременно является центральной точкой вписанной и описанной окружностей.
5. Все боковые рёбра наклонены к плоскости основы под одинаковым углом.
6. Все боковые поверхности имеют одинаковый угол наклона по отношению к основе.

Благодаря всем перечисленным свойствам, выполнение вычислений элементов намного упрощается

Исходя из приведенных свойств, обращаем внимание на два признака:

1. В том случае, когда многоугольник вписывается в окружность, боковые грани будут иметь с основой равные углы.
2. При описании окружности около многоугольника, все рёбра пирамиды, исходящие из вершины, будут иметь равную длину и равные углы с основой.

В основе лежит квадрат

многогранник, у которого в основе лежит квадрат.

У неё четыре боковых грани, которые по своему виду являются равнобедренными.

На плоскости квадрат изображают параллелограммом, но основываются на всех свойствах правильного четырёхугольника.

К примеру, если необходимо связать сторону квадрата с его диагональю, то используют следующую формулу: диагональ равна произведению стороны квадрата на корень квадратный из двух.

В основе лежит правильный треугольник

Правильная треугольная пирамида – многогранник, в основании которого лежит правильный 3-угольник.

Если основание является правильным треугольником, а боковые рёбра равны ребрам основания, то такая фигура называется тетраэдром.

Все грани тетраэдра являются равносторонними 3-угольниками. В данном случае необходимо знать некоторые моменты и не тратить на них время при вычислениях:

• угол наклона ребер к любому основанию равен 60 градусов;
• величина всех внутренних углов граней также составляет 60 градусов;
• любая грань может выступить основанием;
• высоты, проведённые внутри фигуры, это равные элементы.

Формулы объема и площади поверхности пирамиды с примерами расчета

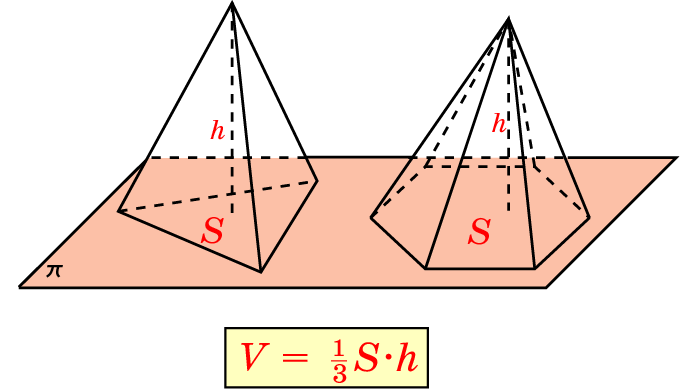
Вычислить объём можно с использованием следующей формулы.

где используются такие обозначения:

S – площадь основания;

Полную площадь поверхности можно вычислить как сумму площадей основания и всех боковых треугольников.

Пример решения задачи

Если стороны основания составляют 3 см, а боковые рёбра — 4 см, то по теореме Пифагора можно определить высоту фигуры.

Сначала по теореме Пифагора находят длину половины диагонали. Она будет равна корню квадратному из 18 (4,25 см), так как является диагональю квадрата.

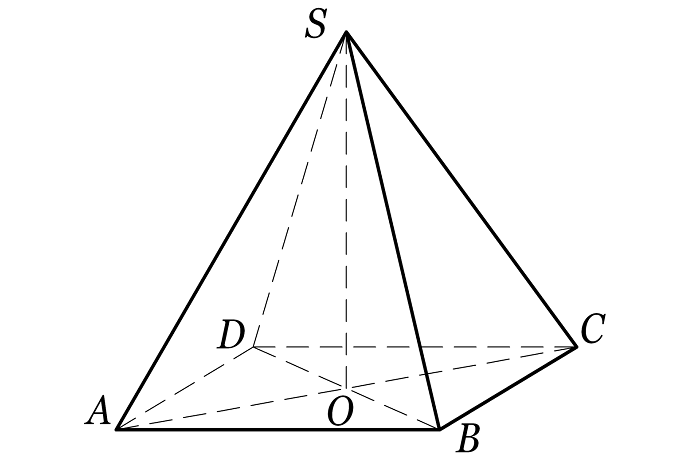
Здесь рассматривается четырехугольная пирамида.

По теореме Пифагора находим высоту. Она будет равна примерно 4,5 см.

Площадь основания составляет 3 * 3 = 9 кв. см. Нужно учесть, что это квадрат со стороной 3 см. Подставив значения в формулу для объёма, получим следующее.

V = (1 / 3) * 9 * 4,5 = 13,5 куб. см.

Для расчёта площади поверхности надо узнать площадь квадратного основания и треугольных боковых сторон. Для этого сначала по теореме Пифагора находят длину апофемы. Она будет равна 4,27 см.

Каждая боковая сторона имеет площадь 12,81 кв. см, а основание — 9 кв. см. Сложив площади всех граней, получим 60,24 кв. см. Посчитать площадь поверхности можно, рассмотрев развертку фигуры.

Виды пирамид

1. Правильная пирамида – основанием фигуры является правильный многоугольник, а ее вершина проецируется в центр основания. Может быть треугольной, четырехугольной (на рисунке ниже), пятиугольной, шестиугольной и т.д.
2. Пирамида с боковым ребром, перпендикулярным основанию – одно из боковых ребер фигуры расположено под прямым углом к плоскости основания. В этом случае данное ребро является высотой пирамиды.
3. Усеченная пирамида – часть пирамиды, оставшаяся между ее основанием и параллельной этому основанию секущей плоскостью.
4. Тетраэдр – это треугольная пирамида, гранями которой являются 4 треугольника, каждый из которых может быть принят за основание. Является правильным (как на рисунке ниже) – если все ребра равны, т.е. все грани – это равносторонние треугольники.

Сечения многогранника

В любом многограннике различают несколько видов сечения плоскостью. Зачастую в школьном курсе геометрии работают с двумя:

• осевое;
• параллельное основе.

Осевое сечение получают при пересечении плоскостью многогранника, которая проходит через вершину, боковые рёбра и ось. В данном случае осью является высота, проведённая из вершины. Секущая плоскость ограничивается линиями пересечения со всеми гранями, в результате получаем треугольник.

Внимание! В правильной пирамиде осевым сечением является равнобедренный треугольник.

К примеру, если в основании лежит квадрат, то сечение параллельно основе также будет квадратом, только меньших размеров.

При решении задач при таком условии используют признаки и свойства подобия фигур, основанные на теореме Фалеса. В первую очередь необходимо определить коэффициент подобия.

Если плоскость проведена параллельно основе, и она отсекает верхнюю часть многогранника, то в нижней части получают правильную усеченную пирамиду. Тогда говорят, что основы усеченного многогранника являются подобными многоугольниками. В этом случае боковые грани являются равнобокими трапециями. Осевым сечением также является равнобокая трапеция.

Для того чтобы определить высоту усеченного многогранника, необходимо провести высоту в осевом сечении, то есть в трапеции.

Элементы пирамиды

Для рисунка выше:

• Основание (четырехугольник ABCD) – грань фигуры, являющая многогранником. Ей не принадлежит вершина.
• Вершина пирамиды (точка E) – общая точка всех боковых граней.
• Боковые грани – треугольники, которые сходятся в вершине. В нашем случае это: AEB, AED, BEC и CED.
• Боковые ребра – стороны боковых граней, за исключением тех, которые принадлежат основанию. Т.е. это AE, BE, CE и DE.
• Высота пирамиды (EF или h) – перпендикуляр, опущенный из вершины пирамиды на ее основание.
• Высота боковой грани (EM) – высота треугольника, являющегося боковой гранью фигуры. В правильной пирамиде называются апофемой.
• Площадь поверхности пирамиды – площадь основания и всех ее боковых граней. Формулы для нахождения площади поверхности (правильной фигуры), а также объема пирамиды представлены в отдельных публикациях.

Развёртка пирамиды – фигура, полученная при “разрезе” пирамиды, т.е. при совмещении всех ее граней в плоскости одной из них. Для правильной четырехугольной пирамиды развертка в плоскости основания выглядит следующим образом.

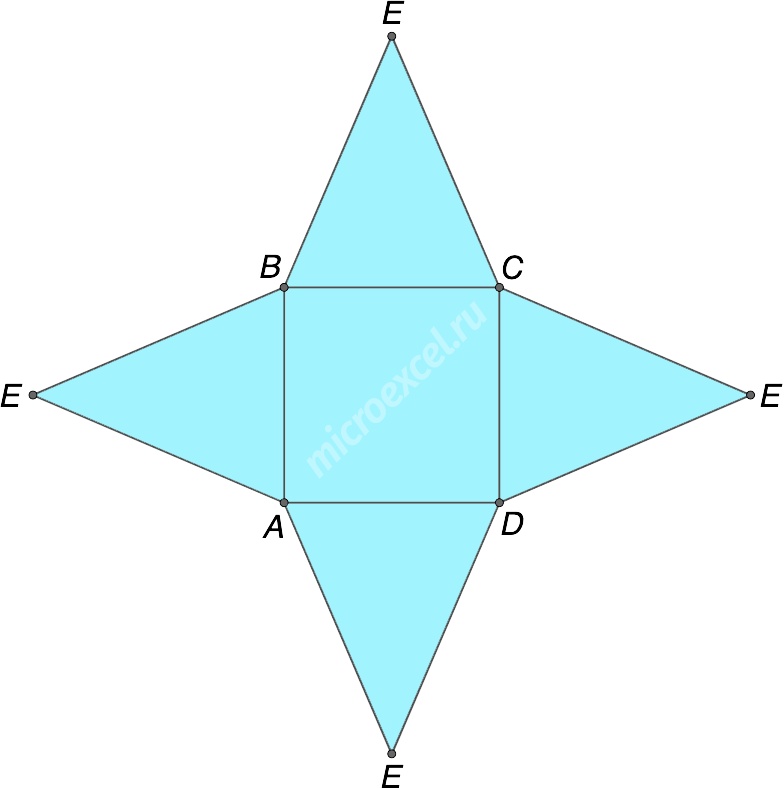
Примечание: свойства пирамиды представлены в отдельной публикации.

Свойства пирамиды

Среди свойств, которыми обладает многоугольник в виде пирамиды, можно отметить следующие:

1. В случае равенства всех боковых ребер фигуры вокруг ее основания можно описать круг, центр которого совпадет с центром основания пирамиды. Кроме того, через эту точку пройдет перпендикуляр, который опустили из вершины многоугольника.
2. Равенство всех ребер пирамиды говорит о том, что они расположены под равными углами к плоскости основания.
3. Равенство боковых ребер будет соблюдаться в том случае, когда ими образованы равные углы с плоскостью основания, либо имеется возможность описать вокруг основания многоугольника круг.
4. При наклоне боковых граней к плоскости основания под одинаковым углом можно вписать круг в основание пирамиды. При этом проекция вершины пирамиды будет совпадать с центральной точкой данной окружности.
5. Равенство апофем боковых граней пирамиды возможно в том случае, когда углы наклона боковых граней к основанию равны.

Свойства правильной пирамиды

Правильную пирамиду характеризуют следующие особенности:

• вершина такой геометрической фигуры расположена на одинаковом расстоянии от всех углов основания;
• равенство всех боковых ребер;
• равенство углов наклона всех боковых ребер к плоскости основания;
• равенство апофем всех боковых граней;
• равенство площадей, которыми обладают все боковые грани;
• для всех граней характерно наличие одинаковых двугранных или плоских углов;
• вокруг такой пирамиды можно описать сферу, центром которой будет являться точка пересечения перпендикуляров, пересекающих середину ребер геометрической фигуры;
• в данный многоугольник можно вписать сферу с центром в точке, в которой пересекаются биссектрисы, выходящие из угла, разделяющего ребро и основание;
• при совпадении центра вписанной сферы с центральной точкой описанной сферы сумма плоских углов при вершине равна π (числу «пи», или 180-ти градусам), или наоборот, один угол соответствует π/n, где n является количеством углов в основании пирамиды.

Виды пирамид

1. Правильная пирамида – основание фигуры представляет собой правильный многоугольник, а его вершина проецируется в центр основания. Он может быть треугольным, четырехугольным (на фото ниже), пятиугольным, шестигранным и т.д.
2. Пирамида с боковой гранью, перпендикулярной основанию – одна из боковых граней фигуры расположена под прямым углом к ​​плоскости основания. В данном случае это ребро является высотой пирамиды.
3. Усеченной пирамидой называют часть пирамиды, которая остается между ее основанием и секущей плоскостью, параллельной этому основанию.
4. Тетраэдр – это треугольная пирамида, гранями которой являются 4 треугольника, каждый из которых можно принять за основание вероятно (как на рисунке ниже) – если все ребра наличия, т.е все грани равнобедренные треугольники.

Правильные пирамиды

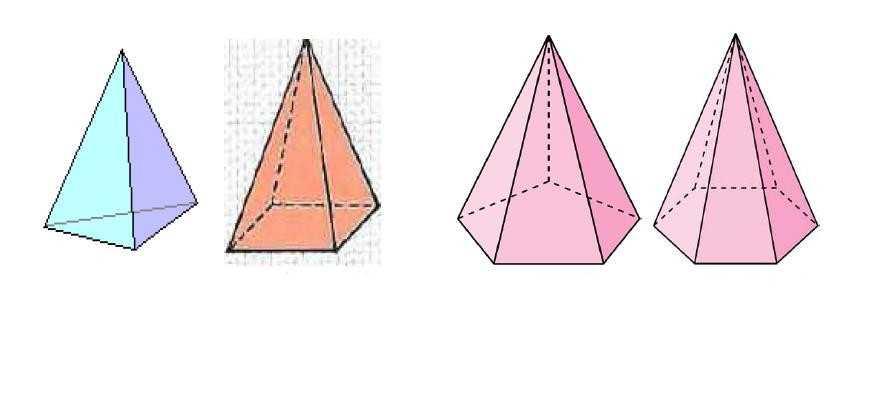
Пирамиды могут быть наклонными и прямыми, правильными и неправильными, выпуклыми и вогнутыми. Все названные типы фигур отличаются друг от друга особенностями полигонального основания и высоты поведения.

Предположим, что имеется пирамида, высота которой (отброшенная от вершины перпендикулярно основанию) приходится на многоугольник точно в его геометрическом центре. В этом случае фигура называется прямой. Если же многоголник из раносторномим, то кроме программ, примида также будет логин. Напоминаем, что центр геометрической плоской фигуры аналогичен центру масс в физике. Для квадрата она совпадает с точкой пересечения диагоналей, а для треугольника — с точкой пересечения медиан.

Пирамиды часто удобно изужать появление их совокупности. Таким образом, боковые ребра правильной пирамиды и ее боковые грани равны между собой. Особым случаем является ситуация, когда боковые грани образованы равносторонними треугольниками.

Далее рассмотрим, по каким формулам следует определять размеры боковых ребер пирамиды — правильного четырехугольника и треугольника.

Треугольная пирамида

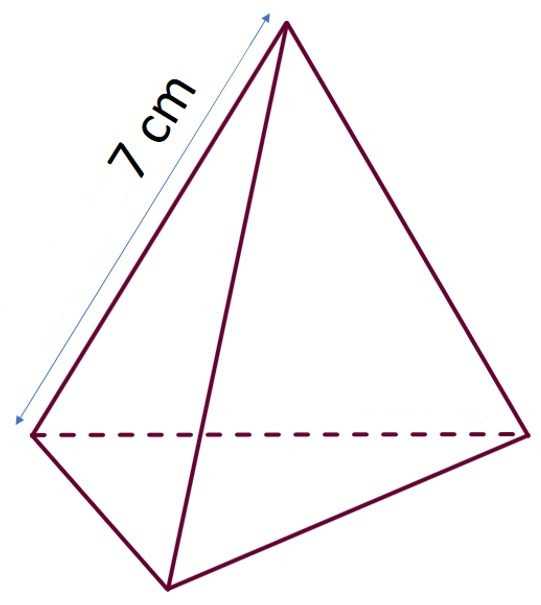
Есть четыре линейных параметра, которые описывают размеры правильной пирамиды. К ним очень строна остановки a, боковое ребро b, высота h и апофема hb. Вот формулы, позволяющие рассчитать длину бокового ребра для правильной треугольной пирамиды. В основе этой фигуры лежит треугольник с равными сторонами, что позволяет написать следующие уравнения:

Обе формулы являются следствием теоремы Пифагора для треугольников, в которых ребро стороны b является гипотенузой.

Четырехугольная пирамида

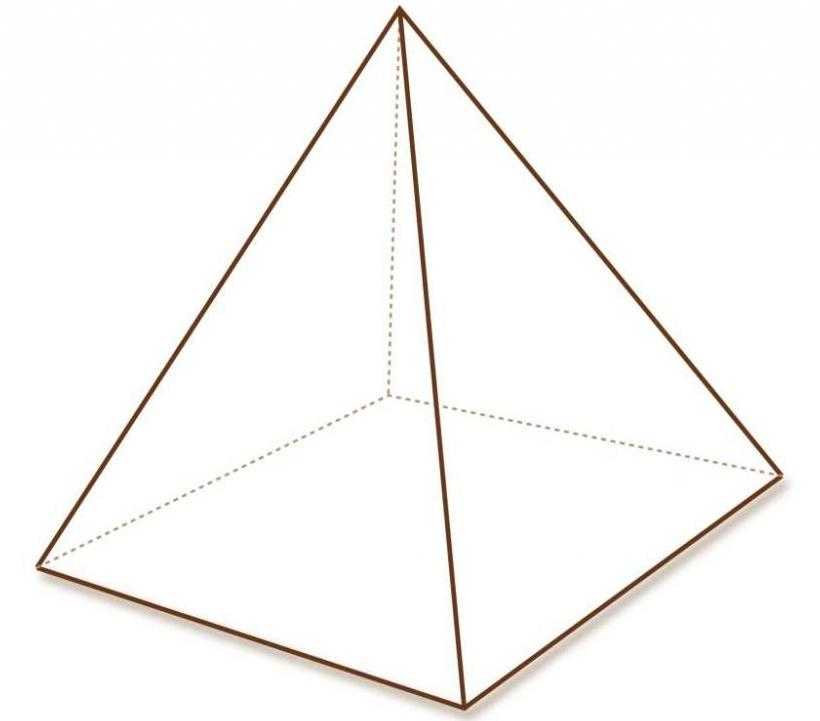
Эта фигура, пожалуй, самая известная среди остальных пирамид благодаря величественным древнеегипетским сооружениям. Боковое ребро квадратной пирамиды можно определить по следующим формулам:

Как и в предыдущем случае, эти выражения являются следствием свойств катетов и гипотенузы прямоугольного треугольника.

Отметим, что формула вычисления бокового ребра правильной квадратной пирамиды через ее апофеум и сторону основания аналогична формуле для треугольной фигуры. Это совпадение не случайно, так как боковые грани обеих пирамид представляют собой равнобедренные треугольники.

Свойства пирамиды

Пирамида с равным боковыми ребрами

Все углы между боковыми ребрами и основанием пирамиды равны.

Свойство 2

Вокруг основания пирамиды можно описать окружность, центр которой будет совпадать с проекцией вершины на ее основание.

• Точка F– проекция вершины E на основание ABCD; одновременно является центром этого основания.
• R– радиус описанной окружности.

Боковые грани пирамиды наклонены к основанию под одинаковым углом

Примечание: для перечисленных выше свойств верны и обратные формулировки. Например, для Свойства 1: если все углы между боковыми ребрами и плоскостью основания пирамиды равны, значит эти ребра имеют одинаковую длину.

Площади поверхностей

Основные геометрические задачи, которые приходится решать в школьном курсе геометрии, это нахождение площадей поверхности и объема у пирамиды.

Значение площади поверхности различают двух видов:

• площади боковых элементов,
• площади всей поверхности.

Из самого названия понятно, о чём идёт речь. Боковая поверхность включает в себя только боковые элементы. Из этого следует, что для ее нахождения необходимо просто сложить площади боковых плоскостей, то есть площади равнобедренных 3-угольников. Попробуем вывести формулу площади боковых элементов:

1. Площадь равнобедренного 3-угольника равна Sтр=1/2(aL), где а – сторона основания, L – апофема.
2. Количество боковых плоскостей зависит от вида k-го угольника в основании. К примеру, правильная четырехугольная пирамида имеет четыре боковые плоскости. Следовательно, необходимо сложить площади четырёх фигур Sбок=1/2(aL)+1/2(aL)+1/2(aL)+1/2(aL)=1/2*4а*L. Выражение упрощено таким способом потому, что значение 4а=Росн, где Росн – периметр основы. А выражение 1/2*Росн является её полупериметром.
3. Итак, делаем вывод, что площадь боковых элементов правильной пирамиды равна произведению полупериметра основания на апофему: Sбок=Росн*L.

Площадь полной поверхности пирамиды состоит из суммы площадей боковых плоскостей и основания: Sп.п.= Sбок+Sосн.

Что касается площади основания, то здесь формула используется соответственно виду многоугольника.

Объем правильной пирамиды равен произведению площади плоскости основания на высоту, разделенную на три: V=1/3*Sосн*Н, где Н – высота многогранника.

Что такое правильная пирамиды в геометрии

Свойства правильной четырехугольной пирамиды

Элементы пирамиды

Для рисунка выше:

• Основание (четырехугольник ABCD) – лицо фигуры, которое многогранно. Ей не перевести вершина.
• Вершина пирамиды (точка Е) является общей точкой всех боковых граней.
• Боковые грани – треугольники, которые сходятся в вершине. В нашем случае это: AEB, AED, BEC и CED.
• Боковые ребра – боковые ребра, кроме тех, которые относятся к основанию. Т.е. Это AE, BE, CE и DE.
• Высота пирамиды (EF или h) – перпендикулярная, опущенная от вершины пирамиды.
• Высота боковых граней (EM) – высота треугольника, являющегося стороной фигуры. В правой пирамиде они называются апофемами.
• Площадь поверхности пирамиды – это площадь основания и всех ее боковых граней. Формулы для нахождения площади поверхности (правильной фигуры) и объема пирамиды представлены в отдельных публикациях.

Развёртка пирамиды – фигура, получная при «разрезе» пирамиды, т.е при совмещении всех ее граней в другом месте из них. Для правильной четырехугольной пирамиды разброс в плоскости основания выглядит так.

Примечание: свойства пирамид представлены в отдельной публикации.

Некоторые свойства пирамиды

1) Если все боковые ребра здоровья, то

— около основания пирамиды можно описать окружность, а вершина пирамиды проецируется в ее центр

– боковые ребра образуют плоские углы с плоским основанием

Правда и наоборот.

Если боковые ребра образуют равные углы с плоскостью основания, то все боковые ребра пирамиды равны.

Если вокруг основания пирамиды можно описать окружность, а вершина пирамиды выступает в ее центр, то все боковые ребра пирамиды равны.

2) Если все грани пирамиды наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, причем вершина пирамиды спроецирована в ее центр

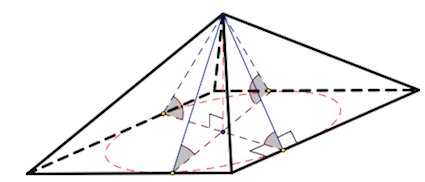
Правда и наоборот.