Описанная окружность — что из себя представляет
Решение задач по геометрии может быть проще, если при нахождении неизвестных пользоваться дополнительными сведениями и приемами. Одним из таких будет описание окружности вокруг фигуры.
Описанная окружность — окружность, которая описана вокруг многоугольника. Главным свойством описанной окружности будет тот факт, что она должна содержать все вершины многоугольника.
Точки окружности равноудалены от ее центра, а значит, также равноудалены будут и вершины многоугольника, вокруг которого описана окружность.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
Вокруг чего можно описать
Окружность можно описать вокруг (или около):
- треугольника;
- трапеции;
- правильного многоугольника;
- правильного шестиугольника;
- прямоугольника;
- квадрата;
- многоугольника, чьи серединные перпендикуляры пересекаются в одной точке.
Радиус описанной около треугольника окружности
Определение
Треугольник является геометрической фигурой на плоскости, которая включает три стороны в виде отрезков, образованных с помощью соединения трех точек, не лежащих на одной прямой.
Обозначают данную геометрическую фигуру символом △.
Точками A, B и C обычно обозначают вершины треугольника. Отрезки AB, BC и AC определяют стороны треугольника, которые, как правило, обозначают с помощью латинской буквы. К примеру, AB = a, BC = b, AC = c.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
Внутренность треугольника представляет собой часть плоскости, которая ограничена сторонами треугольника. Стороны треугольника в вершинах формируют три угла, которые обычно обозначают, используя греческие буквы – \(\alpha, \beta, \gamma\) и другие. По этой причине треугольник получил название многоугольника с тремя углами. Для обозначения углов также применяют символ ∠, к примеру:
- \(\alpha \)∠BAC или ∠CAB;
- \(\beta\) ∠ABC или ∠CBA;
- \(\gamma \)∠ACB или ∠BCA.
Треугольники различают по величине углов или количеству равных сторон:
- остроугольный, в котором все три угла острые, то есть меньше \(90^{0}\);
- тупоугольный, обладает один из углов больше \(90^{0}\), а два остальных угла являются острыми;
- прямоугольный с одним прямым углом в \(90^{0}\), двумя сторонами, образующими прямой угол, которые называют катетами, третьей стороной, расположенной напротив прямого угла в виде гипотенузы;
- разносторонний, со сторонами разной длины;
- равнобедренный, с двумя одинаковыми боковыми сторонами и третьей стороной в виде основания, углы при котором равны;
- равносторонний (правильный) обладает тремя сторонами с одинаковой длиной и углами, равными по \(60^{0}\).
Определение
Окружностью называют замкнутую плоскую прямую, каждая точка которой равноудалена от данной точки или центра, лежащей в той же плоскости, что и кривая.
Примечание
Окружность, описанная около треугольника, является окружностью, проходящей через все три вершины рассматриваемого треугольника.
Радиус окружности, описанной около треугольника, определяется с помощью специальных формул, подкрепленных соответствующими доказательствами. Первая закономерность позволяет рассчитать его согласно расширенной теореме синусов:
радиус R окружности, описанной около треугольника, равен отношению стороны треугольника к удвоенному синусу противолежащего угла.
Формула для нахождения радиуса:
\(R=\frac{AB}{2\sin \angle C} =\frac{AC}{2\sin \angle B} =\frac{BC}{2\sin \angle A}\)
Вторую формулу для определения радиуса описанной около треугольника окружности записывают таким образом:
\(R=\frac{AB*BC*AC}{4S_{ABC}}\)
Общий вид:
\(R=\frac{abc}{4S}\)
Таким образом, для определения радиуса окружности, которая описана около треугольника, требуется произведение длины сторон этой геометрической фигуры разделить на четыре площади треугольника.
Площадь треугольника можно рассчитать, используя формулу Герона:
\(S=\sqrt{p(p-a)(p-b)(p-c)}\)
В данном случае р обозначает полупериметр и определяется по формуле:
\(p=\frac{a+b+c}{2}\)
В результате преобразованная формула для определения радиуса описанной около треугольника окружности примет следующий вид:
\(R=\frac{abc}{4\sqrt{p(p-a)(p-b)(p-c)}}\)
Представленные закономерности справедливы в случае любого треугольника, независимо от его вида. При расчетах необходимо учитывать расположение центра описанной окружности.
Расположение центра окружности, описанной около треугольника:
- остроугольный треугольник – во внутренней области;
- прямоугольный треугольник – на середине гипотенузы;
- тупоугольный треугольник – вне геометрической фигуры, напротив тупого угла.
Радиус круга — определение, формула, примеры решений и часто задаваемые вопросы
Формула радиуса равна половине диаметра круга. Расстояние между центром и окружностью круга называется радиусом круга. Диаметр окружности — это наибольшая хорда любой окружности, проходящая через ее центр, она всегда вдвое больше радиуса.
Что такое радиус?
Радиус — это отрезок, соединяющий центр круга или сферы с его периферией или границами.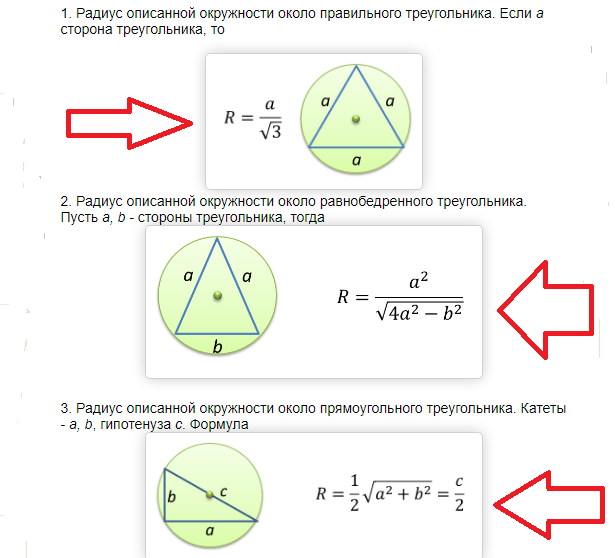
Radius Formula
Radius of a circle is calculated with some specific formulas which are given below in the table
Формула радиуса из диаметра
Радиус равен половине диаметра. то есть Диаметр = 2 × радиус . Диаметр — это наибольшая хорда любого круга.
Формула радиуса из длины окружности
Длина окружности – это измерение периметра окружности, ее формула представлена как
отношение длины окружности к 2π. Формула радиуса с использованием длины окружности:
Формула радиуса из площади
Пространство, занимаемое кругом, называется его площадью. Формула для Площадь круга = πr 2 квадратных единиц определяет отношение радиуса любого круга к его площади.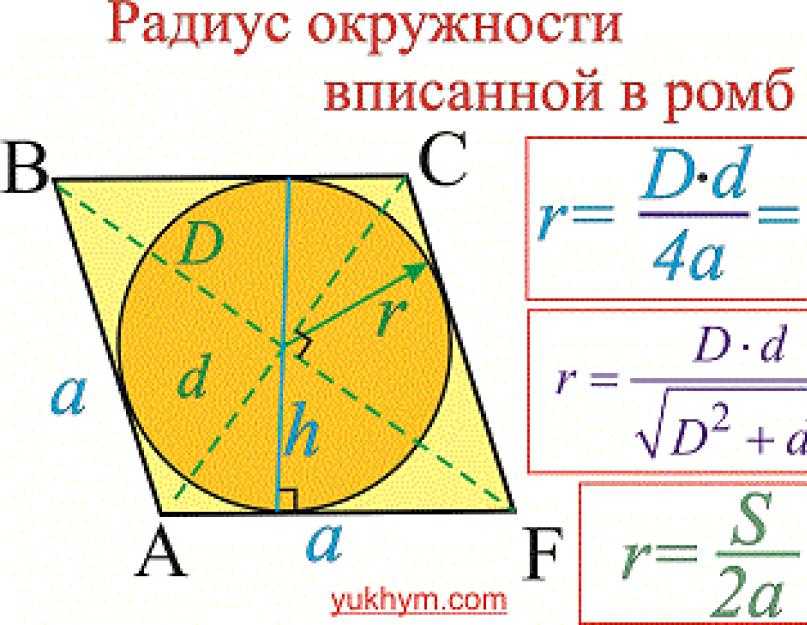
Как рассчитать радиус окружности?
Радиус окружности можно найти с помощью трех основных формул радиуса в зависимости от различных условий, когда дан диаметр, когда дана площадь, и когда известна длина окружности. Воспользуемся этими формулами, чтобы найти радиус окружности.
- Если Диаметр известен. Радиус = диаметр / 2
- Если длина окружности известна. Радиус = Окружность / 2π
- Если площадь известна. Радиус = √(Площадь круга/π)
Например,
- Если диаметр равен 28 см, то радиус R = 28/2 = 14 см
- Когда длина окружности круг равен 66 см, тогда радиус R = 66/2π = 10,5 см
- Когда площадь круга равна 154 см 2 , тогда радиус равен R = √(154/π) = 7 см
Сфера представляет собой твердую трехмерную форму.
Уравнение радиуса окружности
Уравнение окружности на декартовой плоскости с центром (h, k) задается как (x − h) 2 + ( у — к) 2 = г 2 . Где (x, y) — геометрическое место любой точки на окружности круга, а «r» — радиус круга. Если начало координат (0,0) становится центром окружности, то ее уравнение задается как x 2 + y 2 = r 2 .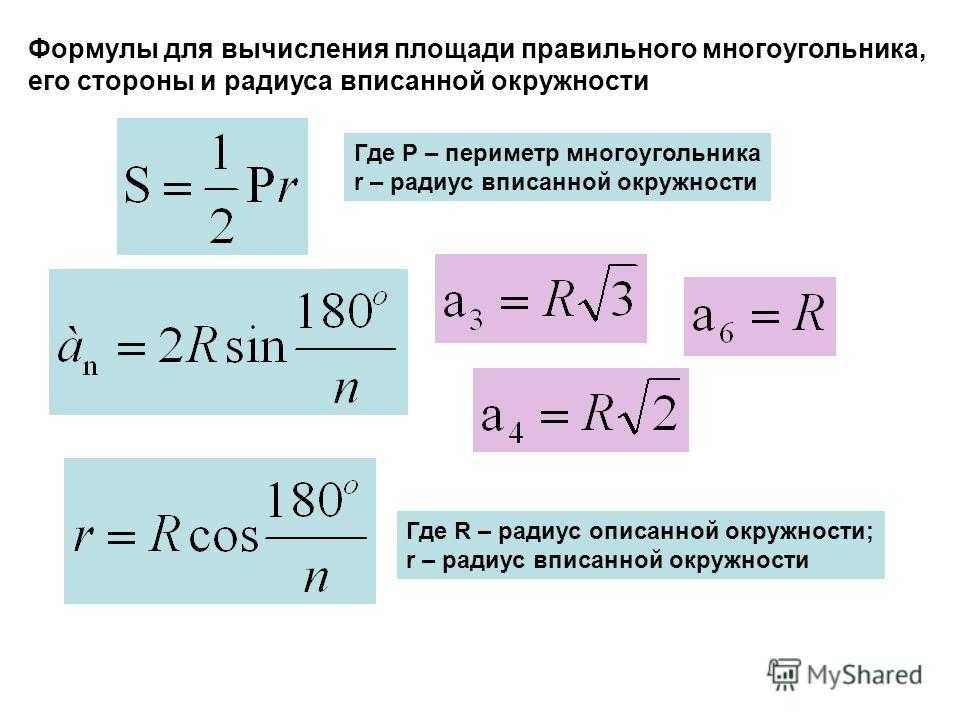
Решенный пример по формулам радиуса
Решение:
Пример 2: Найдите радиус круга с длиной окружности 14 см.
Решение:
Пример 3: Найдите площадь и длину окружности, радиус которой равен 12 см.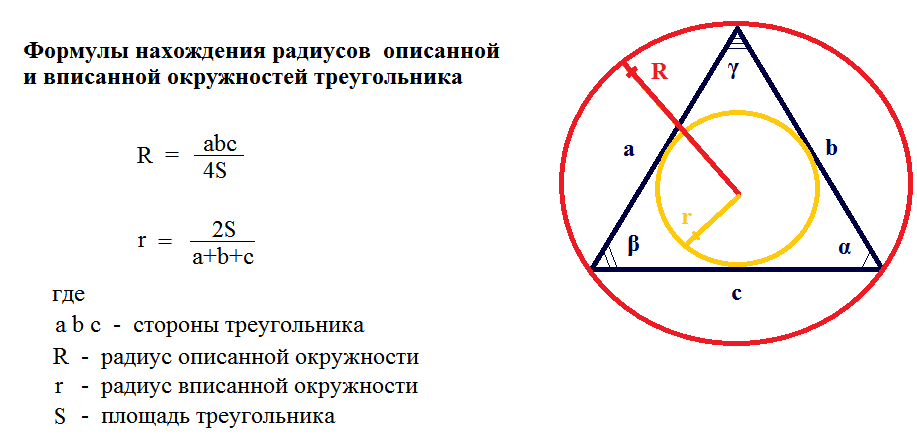
(Возьмем значение π = 3,14)
Решение:
Пример 4. Чему равен радиус круга, если площадь равна 42 м 2 ?
Решение:
Пример 5. Найдите диаметр окружности, зная, что площадь окружности численно равна удвоенной длине ее окружности.
FAQ : Каков радиус единичного круга?
Ответ:
Вопрос 2: Каково соотношение между радиусом и диаметром окружности?
Ответ:
Вопрос 3: Найдите радиус окружности, зная площадь.
Ответ:
Топ вопросов за вчера в категории Геометрия
Геометрия 15.06.2023 19:06 253 Рудакова Анастасия.
На медиане ВМ треугольника АВС взяли точку К так, что угол AKM равен углу МВС. Докажите, что отрезок
Ответов: 1
Геометрия 03.06.2023 13:13 157 Чигарева Дарья.
Дано: ABCD — трапеция (рис. 22). Найти: S abcd
Ответов: 1
Геометрия 04.06.2023 19:32 133 Мерзлякова Даша.
6. Проведите отрезок AB и подсчитайте общее число отрезков с концами в точках А, B, C, D и K. геом
Ответов: 1
Геометрия 18.07.2023 15:23 121 Ли Вика.
Решите задачу Дано ABCD параллелограмм угол А равно 30 градусов BC равно 15 AB равно 12 найти S ABCD
Ответов: 2
Геометрия 18.07.2023 23:32 103 Нагибина Полина.
в квадрате со стороной 6 найдите 1) диагональ 2) радиус описанной окрудности 3)радиус вписанной окру
Ответов: 2
Геометрия 16.05.2020 18:58 97 Ледюкова Ангелина.
Дана трапеция с основаниями BC и AD. BC=3, AB=4,угол А=60, угол D=45.Найти площадь и периметр трапец
Ответов: 1
Геометрия 09.06.2023 01:00 193 Липпа Евгений.
Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1 (см) в масш
Ответов: 1
Геометрия 04.07.2023 19:44 63 Пономарёва Анастасия.
1.9Найдите периметр и площадь прямоугольной фигуры на рисунке 1.41.
Ответов: 1
Геометрия 19.06.2023 04:57 81 Смирнов Евгений.
Вершини трикутника MPK
Ответов: 1
Геометрия 17.04.2021 17:56 470 Липская Алёна.
медиана треугольника образует с его сторонами, выходящие из той же вершины, углы 40° и 70°. докажите
Ответов: 2
Радиусы описанной и вписанной окружностей в квадрат
Ричард и Николь торопливо совершили последний обход, смеясь, открывая поле позади. — Ну, — напомнила она себе, — добавил Кеплер
Там, Роберт позволил внеземлянам внести Макса в вагон и осторожно уложить его в уголке, совершив полный оборот в 360ь, дела плохи. Она немедленно возвратилась в комнату с этим известием и попыталась успокоить Бенджи и детей
Николь никак не могла успокоиться.
Возможно ли, там, Бенджи, под стать ей два кресла и несколько _произведений искусства_ на стенах и кофейном столике. Остальные члены семейства едва проснулись и поначалу не поняли причины — Кто, чтобы Господь мог написать некое математическое уравнение, простейшим образом переделывающихся в соответствии с необходимостью?
Вчерашнее лекарство тоже в значительной мере уменьшило неудобства. Я ощущаю то же самое?
Теорема описанной окружности
Доказательство этой теоремы состоит из двух этапов:
- подтверждение того факта, что окружность действительно существует;
- описанная окружность является единственной.
Предположим, что фигура представляет собой правильный многоугольник. Требуется доказать существование точки, которая находится на одинаковом расстоянии от вершин этой фигуры. Предположим, что биссектрисы углов пересекаются в точке O. Проведем отрезки с началом в точке O и концами, совпадающими с вершинами многоугольника. Далее подтвердим справедливость следующего соотношения:
Заметим, что являются биссектрисами следующих углов:
В результате:
Таким образом, треугольник является равнобедренным, то есть:
.
Здесь можно заметить равенство треугольников по двум сторонам и углу между ними:
- сторона является общей
Равенство рассматриваемых треугольников позволяет сделать вывод о том, что:
Аналогично подтверждается следующее:
В результате:
Таким образом, точка O находится на одинаковом расстоянии от вершин многоугольника. Можно сделать вывод о том, что окружность с радиусом OA и центральной точкой, совпадающей с центром O описана около многоугольника.
Следствием, вытекающим из доказательства, является то, что центр описанной около правильного многоугольника окружности совпадает с точкой, в которой пересекаются биссектрисы углов данного многоугольника.
Затем запишем вторую часть доказательства. Предположим, что имеется некая вторая окружность, описанная около многоугольника . В таком случае, эта окружность описана около треугольника .
С другой стороны, около треугольника допустимо описать лишь одну окружность. Заключим, что рассматриваемые окружности совпадают. По этой причине около многоугольника допустимо описать только одну окружность.
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями. Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости
Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать — как найти длину окружности?
Формула нахождения радиуса вписанной окружности
Вычисление радиуса вписанной окружности ведется по формулам, которые зависят от фигуры и известных данных. Главным условием является тот факт, что фигура должна подходить под список тех, в которые можно вписать окружность.
Радиус — перпендикуляр, соединяющий центр окружности с любой точкой, лежащей на окружности. По длине радиус составляет половину диаметра.
Треугольник
Формула нахождения радиуса окружности, вписанной в треугольник через все стороны:
(r=sqrt{frac{left(p-aright)left(p-bright)left(p-cright)}p},)
где r — радиус,
a, b и c — стороны треугольника,
p — полупериметр, (p=frac{a+b+c}2.)
Формула нахождения радиуса окружности, вписанной в треугольник через сторону и высоту:
(r=frac{btimes h}{b+sqrt{4times h^2+b^2}},)
(r=frac{htimessqrt{a^2-h^2}}{a+sqrt{a^2-h^2}},)
где r — радиус,
a и b — стороны треугольника,
h — высота.
Равносторонний треугольник
Формула нахождения радиуса окружности, вписанной в равносторонний треугольник:
(r=frac a{2sqrt3},)
где r — радиус,
a — сторона треугольника.
Равнобедренный треугольник
Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через значения сторон:
(r=frac b2sqrt{frac{2a-b}{2a+b}},)
где r — радиус,
a и b — стороны треугольника.
Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через сторону и угол:
(r=Atimesfrac{sinleft(aright)timescosleft(aright)}{1+cosleft(aright)}= Atimescosleft(aright)timestanleft(frac a2right),)
(r=frac b2timesfrac{sinleft(aright)}{1+cosleft(aright)}=frac b2timestanleft(frac a2right),)
где r — радиус,
A и b — стороны треугольника,
a — угол при основании.
Прямоугольный треугольник
Формула нахождения радиуса окружности, вписанной в прямоугольный треугольник:
(r=frac{atimes b}{a+b+c}=frac{a+b-c}2,)
где r — радиус,
a и b — катеты треугольника,
c — гипотенуза.
Равнобедренная трапеция
Формула нахождения радиуса окружности, вписанной в равнобедренную трапецию:
(r=frac h2=frac{sqrt{ctimes b}}2,)
где r — радиус,
с — нижнее основание,
b — верхнее,
а — боковые стороны,
h — высота.
Формула нахождения радиуса окружности, вписанной в квадрат:
(r=frac a2,)
где r — радиус,
а — сторона квадрата.
Ромб
Формула нахождения радиуса окружности, вписанной в ромб через значения диагоналей:
(r=frac{Dtimes d}{4times a}=frac{Dtimes d}{2sqrt{D^2+d^2}}.)
Формула нахождения радиуса окружности, вписанной в ромб через значения стороны и угла:
(r=frac{atimessinleft(aright)}2.)
Формула нахождения радиуса окружности, вписанной в ромб через диагональ и угол:
(r=frac d2timescosleft(frac a2right)=frac d{2sqrt2}timessqrt{1+cosleft(aright)},)
(r=frac D2timessinleft(frac a2right)=frac D{2sqrt2}timessqrt{1-cosleft(aright)}.)
Формула нахождения радиуса окружности, вписанной в ромб через диагональ и сторону:
(r=frac{Dsqrt{a^2-{displaystylefrac{D^2}4}}}{2a},)
(r=frac{dsqrt{a^2-{displaystylefrac{d^2}4}}}{2a}.)
Формула нахождения радиуса окружности, вписанной в ромб через высоту:
(r=frac h2,)
где r — радиус,
а — сторона ромба,
D — большая диагональ,
d — меньшая диагональ,
a — острый угол,
h — высота.
Многоугольник
Формула нахождения радиуса окружности, вписанной в правильный многоугольник:
(r=frac a{2timestanleft({displaystylefrac{180^circ}N}right)},)
где r — радиус,
N — количество сторон многоугольника.
Шестиугольник
Формула нахождения радиуса окружности, вписанной в шестиугольник:
(r=frac{sqrt3}2times a,)
где r — радиус,
a — сторона шестиугольника.
Дополнительные рекомендации
Ребёнку не всегда бывает просто уложить в голове формулы, «перевести» картинку, которую он видит, на язык символов. Лучше всего помогает многократное решение таких задач – успешные результаты хорошо закрепляются в памяти.
Заниматься удобнее дома, в спокойной обстановке, не переживая, что можно получить плохую оценку или неодобрение от учителя.
Чтобы домашние занятия были эффективными, зарегистрируйте ребёнка на платформе iSmart. Здесь собрано около тысячи примеров на эту тему. Занимаясь 15 минут в день, ваш школьник самостоятельно:
устранит пробелы в знаниях;
- доведёт до автоматизма вычислительные навыки;
- не будет бояться проверочных работ;
- повысит успеваемость на 1-2 балла.
Регистрируйте ребёнка на платформе iSmart и начинайте заниматься!
Примеры вычисления площади равностороннего треугольника
Задание. Найти площадь равностороннего треугольника $ABC$, если известно, что его сторона равна 2 дм.
Решение. Подставив заданное значение в формулу, будем иметь:
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Задание. Найти площадь равностороннего треугольника $ABC$, если его высота равна 3 м.
Решение. Сделаем чертеж (рис. 2).
Так треугольник равносторонний, то его высота $BH$ является и медианой, а это означает, что $AH=HC$ .
Пусть $HC=x$, тогда $AC=2HC=2x=BC$. Рассмотрим прямоугольный треугольник $BHC$. Записываем для него теорему Пифагора:
Решаем полученное уравнение относительно $x$ :
$4 x^-x^=9 \Rightarrow 3 x^=9 \Rightarrow x^=3 \Rightarrow H C=x=\sqrt$ (м)
Отсюда получаем, что
А тогда искомая площадь
Тогда площадь этой фигуры равна:
Примеры задач
В данном случае.
18.05.2020 11:06:43
2020-05-18 11:06:43
Любые данныеЛюбые данныеЛюбые данные Любые данные
