Площадь и объём поверхности шара

Введение понятия «шар»

Шар — это тело (рис. 3), ограниченное некой сферической поверхностью. Что за «сферическая поверхность», станет ясно из ее определения: это геометрическое место всех точек на поверхности, расстояние от которых до заданной точки (центра) не превышает некоего неотрицательного числа, называемого радиусом. Как видим, понятия круга и сферической поверхности аналогичны, только разнятся пространства, в которых они находятся. Если изобразить шар в двумерном пространстве, мы получаем круг, границей которого является окружность (у шара граница — сферическая поверхность). На рисунке мы видим сферическую поверхность с радиусами ОА = ОВ.

Формулы исчисления объёма шара и площади его поверхности

Шар образуется при вращении вокруг неподвижного диаметра полукруга или круга. Для вычислений разных параметров данного объекта понадобится не так уж много данных.

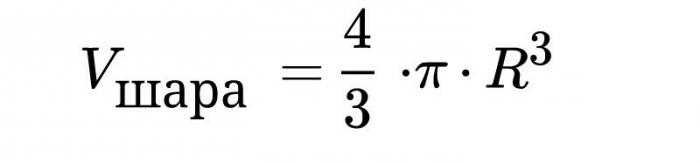
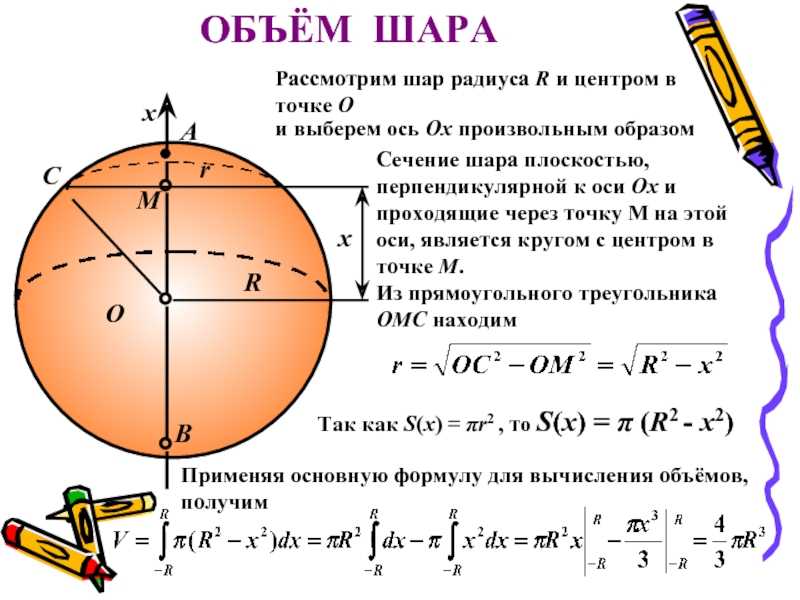
Объем шара, формула для исчисления которого указана выше, выведен посредством интегрирования. Разберемся по пунктам.

Рассматриваем круг в двумерной плоскости, ведь, как было сказано выше, именно круг лежит в основе построения шара. Используем лишь его четвертую часть (рисунок 10).

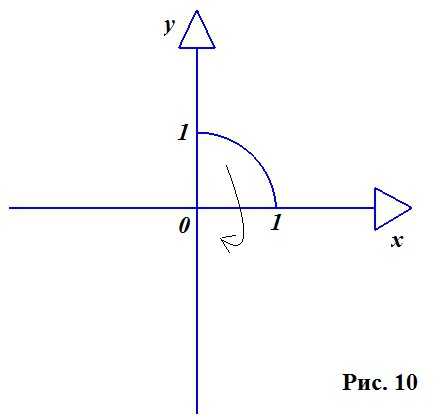
Берем круг с единичным радиусом и центром в начале координат. Уравнение такого круга выглядит следующим образом: Х 2 + У 2 = R 2 . Выражаем отсюда У: У 2 = R 2 — Х 2 .

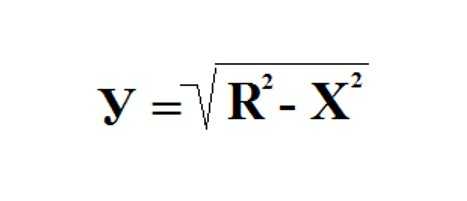
Обязательно отметим, что полученная функция неотрицательная, непрерывная и убывающая на отрезке Х (0; R), ведь значение Х в том случае, когда мы рассматриваем четверть круга, лежит от нуля до значения радиуса, то есть до единицы.

Следующее, что мы делаем, это вращаем нашу четверть круга вокруг оси абсцисс. В результате мы получим полушар. Чтобы определить его объём, прибегнем к методам интегрирования.

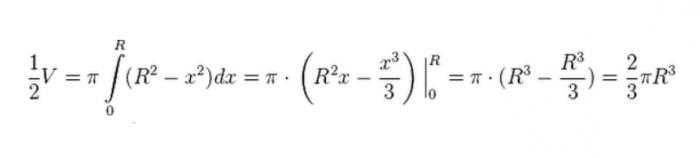
Так как это объём лишь полушара, увеличиваем результат в два раза, откуда получаем, что объем шара равен:

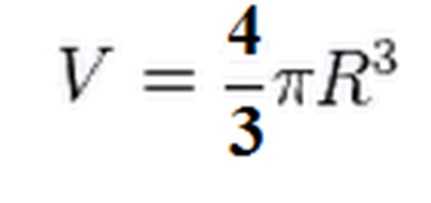
Что такое шар?

В стереометрии есть большой раздел, который называется фигуры вращения. Об этом редко говорят в школе, но плоские фигуры можно вращать вокруг какой-либо оси или точки. Так получаются объемные фигуры.

Стереометрия это наука о фигурах в пространстве. Простейшими единицами стереометрии является точка, прямая и плоскость.

Например, цилиндр образован вращением прямоугольника или квадрата. Поэтому, если рассечь цилиндр плоскостью, то сечение примет форму того самого квадрата или прямоугольника, который вращали, чтобы получить фигуру.

Так же и шар образован вращением. Как не трудно догадаться, основной для шара послужил круг. Причем сразу стоит сказать, что именно круг, а не окружность.

Следует понимать, что круг и окружность разные фигуры. Так окружность представляет собой набор точек равноудаленных от центра. Переводя на более простой язык окружность – это сама линия и центр окружности. А круг включает в себя и все внутреннее пространство. У окружности не может быть площади.

То есть, шар имеет какое-то внутренне заполненное пространство. Интересно, что сфера так же имеет пространство внутри, только условно полое.

Шар

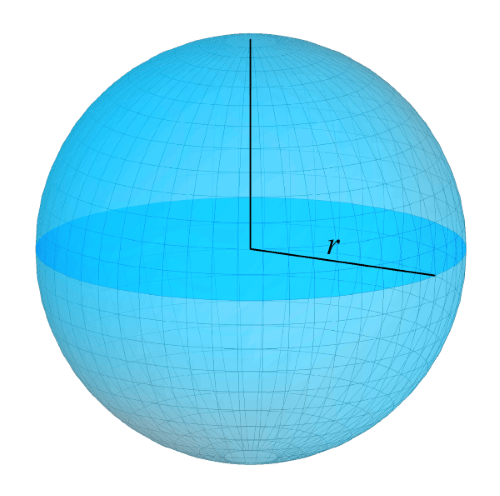
Шаром радиуса R с центром в точке О в геометрии называют тело, которое создано всеми точками пространство, имеющими общее свойство. Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра. Если мы рассмотрим только те точки, которые равноудалены от центра шара — мы будем рассматривать его поверхность или оболочку шара.

Как можно получить шар? Мы можем вырезать из бумаги круг и начать его вращать вокруг его же диаметра. То есть диаметр круга будет осью вращения. Образованная фигура — будет шар. Поэтому шар называют также телом вращения. Потому что он может быть образован путем вращения плоской фигуры — круга.

Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.

В Древней Греции умели не только работать с шаром и сферой, как с геометрическими фигурами, например, использовать их при строительстве, а также умели расчитывать площадь поверхности шара и объем шара.

Сферой иначе называется поверхность шара. Сфера — это не тело — это поверхность тела вращения. Однако так как и Земля и многие тела имеют сферическую форму, например капля воды, то изучение геометрических соотношений внутри сферы получило большое распространение.

Например, если мы соединим две точки сферы между собой прямой линией, то эта прямая линия назовется хордой, а если эта хорда пройдет через центр сферы, который совпадает с центром шара, то хорда назовется диаметром сферы.

Если мы проведем прямую линию, которая коснется сферы всего в одной точке, то эта линия будет называться касательной. Кроме того, эта касательная к сфере в этой точке будет перпендикулярна к радиусу сферы, проведенному в точку касания.

Если мы продолжим хорду до прямой в одну и другую сторону от сферы, то эта хорда станет называться секущей. Или можно сказать иначе — секущая к сфере содержит в себе ее хорду.

Площадь сферы

Замечание 2

Площадь сферы вычисляется по формуле:

$S = 4πR^2$.

Для вычисления площади сферы нужно ознакомиться с понятием степени числа, зная определение которой формулу площади сферы можно переписать в следующем виде:

$S = 4πR^2= 4πR \cdot R$.

Пример 3

Вычислить площадь сферы, если её радиус равен $2 \frac{4}{5}$ см.

Решение.

Воспользуемся формулой площади сферы:

$S = 4πR^2$.

Подставим значение радиуса в формулу и, используя преобразование дробей и правила умножения дробей, найдем результат:

$S=4πR^2=4 \cdot 3,14 \cdot (2 \frac{4}{5})^2=4 \cdot 3,14 \cdot (\frac{14}{5})^2=4 \cdot 3,14 \cdot \frac{196}{25}=\frac{4 \cdot 3,14 \cdot 196}{25}=\frac{2461,76}{25}≈98,47 \ см^2$.

Ответ: $S≈98,47 \ см^2$.

Сечения в сфере (шаре)

Любое сечение сферы является кругом. Если оно проходит через центр шара, то называется большим кругом (окружность с диаметром АВ), остальные сечения — малыми кругами (окружность с диаметром DC).

Площадь данных кругов вычисляется по следующим формулам:

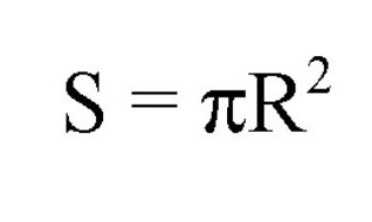
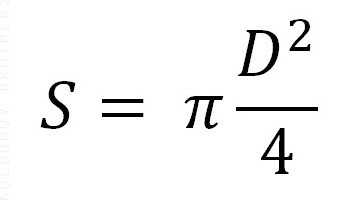
Здесь S — это обозначение площади, R — радиуса, D — диаметра. Также присутствует константа, равная 3,14. Но не стоит путать, что для исчисления площади большого круга используют радиус или диаметр самого шара (сферы), а для определения площади требуются размеры радиуса именно малой окружности.

Таких сечений, которые проходят через две точки одного диаметра, лежащих на границе шара, можно провести бесчисленное число. Как пример — наша планета: две точки на Северном и Южном полюсах, которые являются концами земной оси, а в геометрическом смысле — концами диаметра, и меридианы, которые проходят через эти две точки (рисунок 7). То есть число больших кругов у сферы по количеству стремится к бесконечности.

Примеры из жизни

Пушечные ядра

Допустим, вы хотите узнать, сколько чугуна необходимо для отливки пушечного ядра шестифутового калибра. Вы знаете, что диаметр такого ядра составляет 9,6 сантиметров. Введите это число в ячейку калькулятора «Диаметр», и вы получите ответ в виде

Таким образом, для выплавки пушечного ядра заданного калибра вам понадобится 463 кубических сантиметров или 0,463 литра чугуна.

Воздушные шары

Пусть вам любопытно, сколько воздуха необходимо для накачки воздушного шара идеальной сферической формы. Вы знаете, что радиус выбранного шарика составляет 10 см. Вбейте это значение в ячейку калькулятора «Радиус» и вы получите результат

Это означает, что для накачки одного такого шара вам понадобится 4188 кубических сантиметров или 4,18 литров воздуха.

Объем шара через радиус

{V= dfrac{4}{3}pi r^3}

Формула для нахождения объема шара через радиус: {V= dfrac{4}{3}pi r^3}, где r — радиус шара.

Шар, сфера и их части

      Введем следующие определения, связанные с шаром, сферой и их частями.

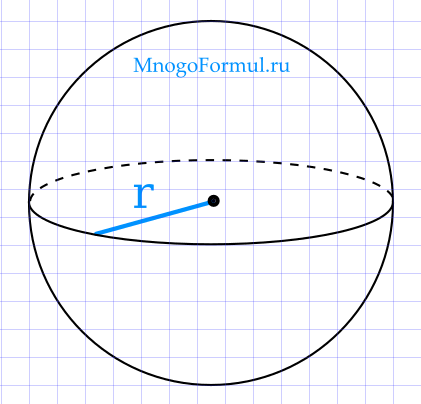
      Определение 1. Сферой с центром в точке   O   и радиусом   r   называют множество точек, расстояние от которых до точки   O   равно   r   (рис. 1).

      Определение 2. Шаром с центром в точке   O   и радиусом   r   называют множество точек, расстояние от которых до точки   O   не превосходит   r   (рис. 1).

Рис.1

      Таким образом, сфера с центром в точке   O   и радиусом   r   является поверхностью шара с центром в точке   O   и радиусом   r.

      Замечание. Радиусом сферы (радиусом шара) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы (радиусом шара).

      Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).

      Определение 4. Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями параллельными плоскостями   (рис. 2).

Рис.2

      Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.

      Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.

      Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.

      Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя.

      Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).

      Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).

Рис.3

      Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.

      Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента.

Рис.4

      По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).

Рис.5

      Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).

Рис.6

      Высотой шарового сектора называют высоту его сферического сегмента.

      Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы.

Советуем посмотреть:

Предмет стереометрии

Параллельность и перпендикулярность прямых и плоскостей в пространстве

Многогранник

Призма

Параллелепипед

Объём тела

Свойства прямоугольного параллелепипеда

Пирамида

Цилиндр

Конус

Многогранники

Инструкция:

• Начнем с примера, когда формула объема шара нам не понадобится — представим, что у нас есть возможность произвести вычисления практическим путем
  
  . Один из наиболее простых способов это сделать — последовать по стопам Архимеда, определив объем не самого шара непосредственно, а вытесненной им воды
  
  . Для этого нужно положить его в емкость, подходящую по размерам, предварительно отметив уровень воды. Погрузив сферу целиком в жидкость, сделайте повторные измерения. Теперь осталось найти разницу
  
  между получившимися цифрами. Конечно, лучше всего будет поместить шар в емкость с делениями, к примеру, в мерный стакан
  
  — если позволяет размер. Таким образом, мы сразу получим нужную характеристику — обычно деления показаны в миллилитрах. В ином случае, просто переведите число в кубические метры.
• Если вы уверены в том, из какого именно материала сделана сфера, постарайтесь определить ее плотность
  
  — эта информация наверняка найдется на просторах всемирной сети. В этой ситуации от вас потребуется лишь взвесить данную фигуру, после чего воспользоваться простой формулой объема шара, разделив вес предмета на его плотность: V=m/p
  .
• Может случиться, что предыдущие варианты вам недоступны. Не отчаивайтесь — если есть возможность узнать радиус шара, к нам на помощь придет нужная формула, более сложная, чем предыдущая, но доступная. Нам необходимо умножить число Пи на 4, после чего перемножить получившееся число на значение радиуса в кубе. В итоге разделите все это на 3, и получите объем шара: V=4*π*r³/3
  . Разберем простой пример: радиус сферы — 30 см
  ., тогда объем фигуры будет составлять: 4*3,14*30³/3 = 11340см³ ≈ 0,113м³.
  
• Бывает и так, что гораздо легче найти диаметр фигуры
  
  , нежели его радиус. Этот вариант даже лучше — можно не производить таких сложных вычислений, формула становится значительно проще. Нам нужно будет лишь умножить диаметр в кубе на число Пи, после чего разделить получившееся число на шесть: V=π*d³/6
  . К примеру, вы узнали, что диаметр вашей сферы составляет 25 см., тогда ее объем будет равняться: 3,14*25³/6 = 8177,08333см³ ≈ 0,818м³.
  

Шар и сфера — это прежде всего геометрические фигуры, и если шар — это геометрическое тело, то сфера — это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.

Впоследствии когда было открыто, что Земля — это шар, а небо — небесная сфера, получило развитие новое увлекательное направление в геометрии — геометрия на сфере или сферическая геометрия. Для того, чтобы рассуждать о размере и объеме шара, нужно сначала дать ему определение.

Шаровый сектор

Определение. Тело, получаемое от вращения (черт. 146) кругового сектора (COD) вокруг диаметра (АВ), не пересекающего ограничивающую его дугу, называется шаровым сектором. Это тело ограничено боковыми поверхностями двух конусов и поверхностью шарового пояса; последняя называется основанием шарового сектора. Один из радиусов кругового сектора может совпадать с осью вращения; например, сектор АОС, вращаясь вокруг АО, производит шаровой сектор ОСАС₁, ограниченный боковой поверхностью конуса и сегментной поверхностью. Для нахождения объёма шарового сектора и целого шара мы предварительно докажем следующую лемму.

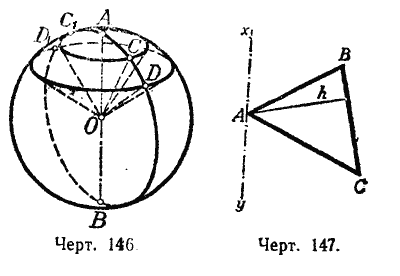
Лемма. Если \(\Delta\)ABC (черт. 147) вращается вокруг оси ху, которая лежит в плоскости треугольника, проходит через его вершину А, но не пересекает стороны ВС, то объём тела, получаемого при этом вращении, равен произведению поверхности, образуемой противоположной стороной ВС, на одну треть высоты h, опущенной на эту cторону.

При доказательстве рассмотрим три случая:

1) Ось совпадает со стороной АВ (черт. 148).

В этом случае искомый объём равен сумме объёмов двух конусов, получаемых вращением прямоугольных треугольников BCD и DCA. Первый объём равен 1/₃ π CD2 • DB, а второй 1/₃ π CD2 • DA; поэтому объём, образованный вращением ABC, равен 1/₃ π CD2 (DB+DA) = 1/₃ π CD • CD • BA

Произведение CD • BA равно ВС • h, так как каждое из этих произведений выражает двойную площадь /\ ABC ; поэтому

объём ABC = 1/₃ π CD • BC• h.

Но произведение π CD • BC равно боковой поверхности конуса BDC; значит,

объём ABC = (поверхность BC)• 1/₃ h.

2) Ось не совпадает с АВ и не параллельна ВС (черт. 149).

В этом случае искомый объём равен разности объёмов тел, производимых вращением треугольников АМС и АМВ. По доказанному в первом случае

объём AMС = 1/₃ h • (поверхность МС), объём AMB = 1/₃ h • (поверхность MB);

следовательно,

объём ABC = 1/₃ h • (поверхность МС-поверхность МВ) = 1/₃ h • (поверхность ВС).

3) Ось параллельна стороне ВС (черт. 150).

Тогда искомый объём равен объёму, производимому вращением DEBC, без суммы объёмов, производимых вращением треугольников АЕВ и ACD; первый из них равен π DC2 • ED; второй 1/₃ π EB2 • EA и третий 1/₃ π DC2 • AD.

Приняв теперь во внимание, что ЕВ = DC, получим:

объём АВС = π DC2 [ED — 1/₃(ЕА + AD)] = π DC2( ED -1/₃ED ) = 2/₃ • π DC2• ED.

Произведение 2π DC• ED выражает боковую поверхность цилиндра, образуемую стороной ВС; поэтому

объём АBС = (поверхность BC)• 1/₃DC = (поверхность BC) • 1/₃h.

Объем шарового сектора

Определение. За величину объёма шарового сектора, получаемого вращением вокруг диаметра (ЕF, черт. 151) кругового сектора (AOD), принимается предел, к которому стремится объём тела, образуемого вращением многоугольного сектора, который ограничен крайними радиусами (ОА и OD) и правильной ломаной линией (ABCD), вписанной в дугу кругового сектора, когда число сторон её неограниченно увеличивается.

Теорема. Объём шарового сектора равен произведению поверхности соответствующего шарового пояса (или соответствующей сегментной поверхности) на треть радиуса.

Пусть шаровой сектор производится вращением вокруг диаметра ЕF (черт. 151) сектора AOD.

Определим его объём V. Для этого впишем в дугу AD правильную ломаную линию ABCD с произвольным числом сторон. Многоугольный сектор OABCD образует при вращении некоторое тело, объём которого обозначим буквой V₁. Объём этот есть сумма объёмов тел, получаемых вращением треугольников ОАВ, ОВС, OCD вокруг оси ЕF.

Применим к этим объёмам лемму, доказанную ранее, причём заметим, что высоты треугольников равны апофеме а вписанной ломаной. Согласно этой лемме будем иметь:

V₁= (поверхность АВ) • a₃+ (поверхность ВС) • a₃ + … = (поверхность ABCD) • a₃ .

Вообразим теперь, что число сторон ломаной линии неограниченно увеличивается. При этом условии поверхность ABCD стремится к пределу, именно к поверхности шарового пояса AD, а апофема а имеет пределом радиус R; следовательно,

V = пределу V₁ = (поверхность пояса AD) • R₃.

Замечание. Теорема и её доказательство не зависят от того, будет ли один из радиусов кругового сектора совпадать с осью вращения или нет.

Правило встречается в следующих упражнениях:

7 класс

Задание 1224, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1227, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1228, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1230, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1231, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 24, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 25, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 26, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1252, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1254, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Сфера

Древние мыслители и ученые с помощью сферической формы, совершенство которой издавна привлекало их внимание, пытались объяснить гармонию окружающего мира. Например, древние греки представляли вращающуюся хрустальную сферу, к которой были прикреплены звёзды

Древнегреческие ученые создавали космологические модели Земли, которые имели сферическую форму и к которым были прикреплены вращающиеся сферы – планеты.

Определение 3

Поверхность шара называется сферой.

Примерами сферы можно назвать волейбольный мяч, теннисный мяч.

Невозможно развернуть сферу на плоскости. Например, на географических картах видно, что полярные области растянуты, изображены с искажением.

Сфера, как и шар, имеет центр, радиус и диаметр.

Для сферы можно вычислить площадь ее поверхности.

Как найти объем сферы

Все материалы по математике для старших классов

8 Диагностические тесты
613 практических тестов
Вопрос дня
Карточки
Learn by Concept

← Предыдущая 1 2 Следующая →

Справка по математике для средней школы »
Геометрия »
Твердая геометрия »
Сферы »
Как найти объем сферы

Каков объем сферы с радиусом ?

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы найти объем сферы, вы должны сначала узнать уравнение объема сферы.

В этом уравнении равно радиусу. Мы можем подставить заданный радиус из вопроса в уравнение для .

Теперь мы просто находим .

Объем сферы .

Сообщить об ошибке

Каков объем сферы с радиусом 4? (Округлите до десятых)

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы найти объем сферы, вы должны сначала узнать уравнение объема сферы.

Уравнение:

Затем подставьте радиус в уравнение, чтобы получить

Затем кубируйте радиус, чтобы получить

Умножьте ответ на  и  , чтобы получить .

Ответ .

Сообщить об ошибке

Объем сферы определяется как В = (4/3) πr 3 , а площадь поверхности определяется как A = 4 πr 90834 90.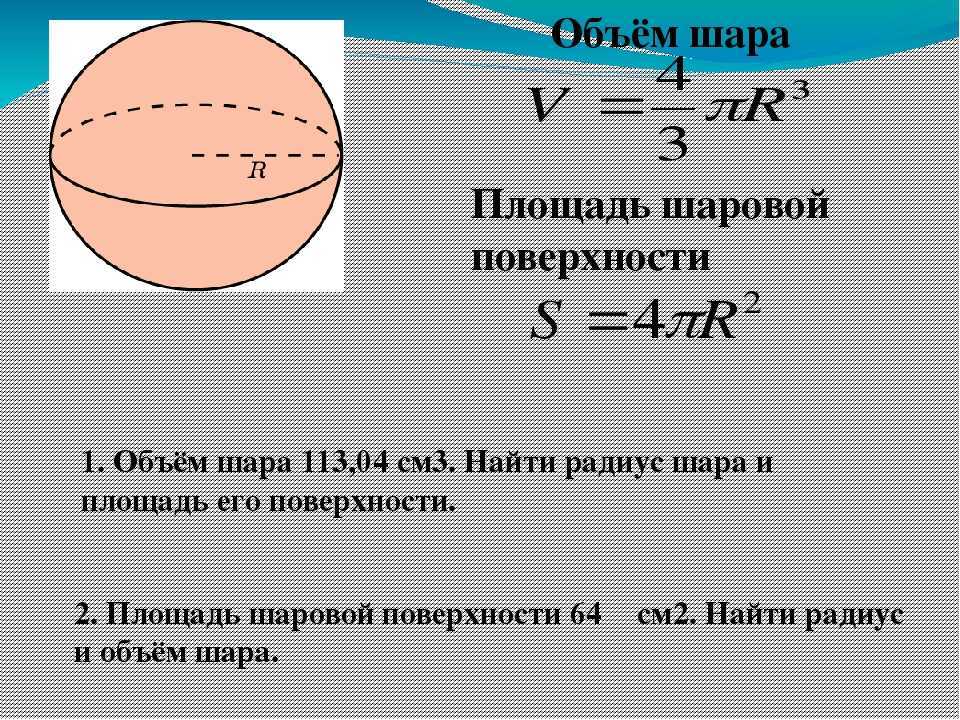

π

Возможные ответы:

615 π

683 π

300 π

750 π

Правильный ответ:

683 π

Объяснение:

Зная площадь поверхности, мы можем найти радиус, а затем найти объем.

4 πr 2 = 256 π

4 R 2 = 256

R 9008 2 = 64

R = 8 2 = 64

r 9000 = 8 2 = 64

R 9000 = 8 2 = 64

R 9000 = 8 2 = 64

R 2 = 64

R 0005

Теперь решите уравнение объема, подставив вместо r :

В = (4/3) π (8) 3

В 9003)8 = (02 1/7007 В 9003)8 = (4/3) π В 9003)8

В = (2048/3) π

В = 683 π

Сообщить об ошибке Найдите объем бейсбольного мяча в кубических сантиметрах.

Возможные ответы:

Недостаточно информации для решения

Правильный ответ:

Объяснение:

Чтобы найти объем сферы, используйте формулу

Нам дан диаметр бейсбольного мяча, который необходимо преобразовать в его радиус.

Теперь мы можем найти объем.

Преобразование в сантиметры.

Если вы пришли к , значит, вы не преобразовали диаметр в радиус.

Сообщить об ошибке

Каков объем сферы, радиус которой .

Возможные ответы:

Недостаточно информации для решения

Правильный ответ:6

5
Расшифровка:

Чтобы найти объем сферы, используйте формулу

Нам дан радиус сферы, .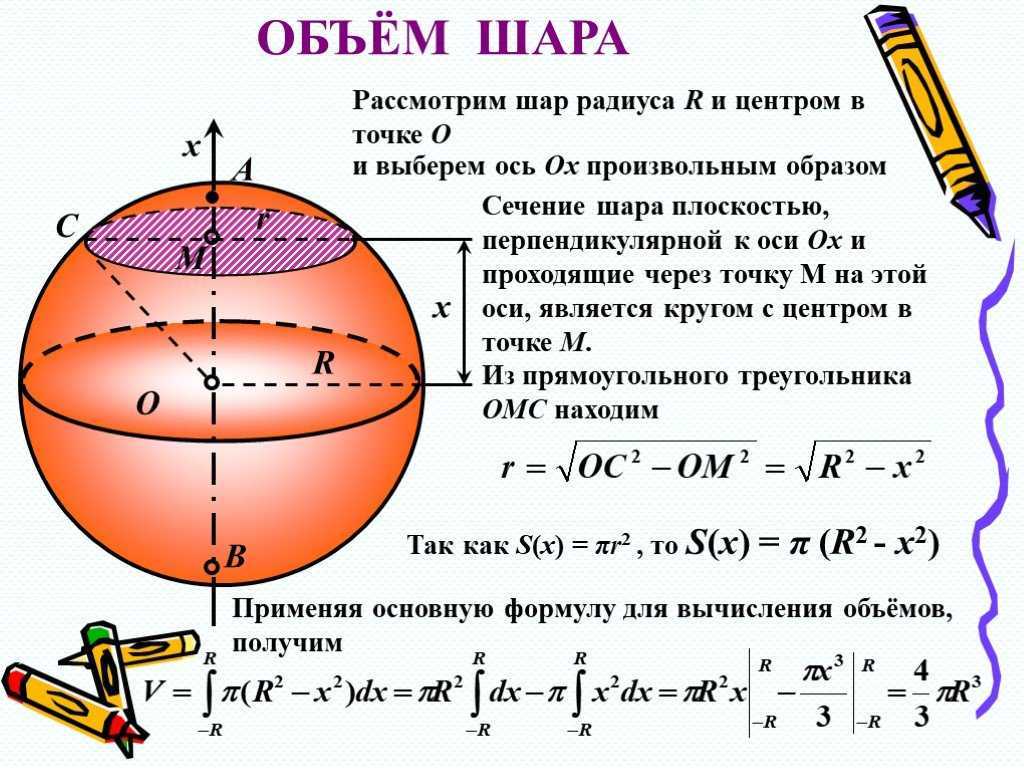

Следовательно, мы можем найти объем.

Если вы подсчитали, что объем будет  тогда вы умножили на , а не на .

Сообщить об ошибке

Определить с точностью до десятой доли кубического сантиметра объем сферы с площадью поверхности 1000 квадратных сантиметров.

Возможные ответы:

Правильный ответ:

Объяснение:

Площадь поверхности сферы с точки зрения его радиуса составляет

Заменить и решить для:

Замена в формуле для объема:

Сообщить об ошибке

Найдите объем следующей сферы.

Возможные ответы:

Правильный ответ:

Объяснение:

Формула объема сферы:

где  это радиус сферы.

Подставив наши значения, мы получим:

Сообщить об ошибке

Найдите объем следующей сферы.

Возможные ответы:

Правильный ответ:

Объяснение:

Формула объема сферы:

Где – радиус сферы

Подставив наши значения, мы получим:

Сообщить об ошибке

Официальная окружность баскетбольного мяча NBA должна быть 2 дюйма. и весить 22 унции. Каков примерный объем баскетбольного мяча? Помните, что объем сферы рассчитывается как V=(4πr 3 )/3

Возможные ответы:

138,43 куб.дюйма

434,19 куб.дюйма

3468,05 куб. дюймов

8557,46 куб. дюймов

92,48 куб.дюйма

Правильный ответ:

434,19 куб.

Пояснение:

Чтобы найти ответ, воспользуемся формулой: C=2πr. Нам дано, что C = 29,5. Таким образом, мы можем подключиться, чтобы получить = 2πr, а затем умножить 2π, чтобы получить 29,5 = (6,28)r. Наконец, мы делим обе части на 6,28, чтобы получить 4,70 = r. Затем мы подставим в формулу объема V=(4π〖(4.7)〗 3 ) / 3   (Информация о 22 унциях бесполезна) 

Сообщить об ошибке

Каков объем сферы диаметром ?

Возможные ответы:

Правильный ответ:

Объяснение:

Формула объема сферы: .

Задача дает нам диаметр, а не радиус. Поскольку диаметр в два раза больше радиуса или , мы можем найти радиус.

Теперь подставьте это в наше исходное уравнение.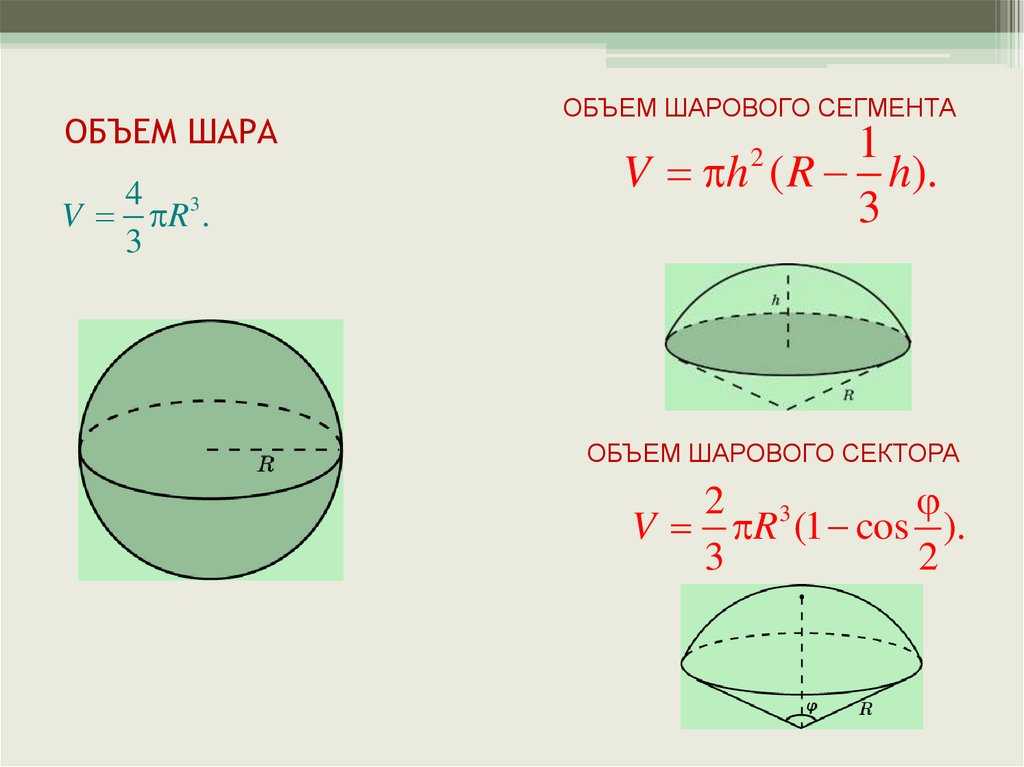

Сообщить об ошибке

← Предыдущая 1 2 Следующая →

Уведомление об авторских правах
613 практических тестов
Вопрос дня
Карточки
Learn by Concept

Калькулятор объема сферы

Введение в калькулятор объема сферы

Объем сферы определяется ее формулой, в которой в основном рассматривается ее радиус (расстояние от середины сферы до любых точек на ее поверхности). Радиус в объеме сферы можно описать как множество всех точек, расположенных на расстоянии «r» от центра точки. Он абсолютно симметричен и не имеет ни ребер, ни вершин.

Формула для нахождения площади поверхности сферы приведена ниже: 92$$

Где,

• r – радиус площади поверхности сферы.
• π значение числа пи равно 3,14 или 3,14159. Это отношение длины окружности любого круга к диаметру круга.

Для расчета объема сферы этот калькулятор объема сферы выполняет формулу, требуя только значение радиуса. И вся формула решается этим онлайн-инструментом. Этот объемный сферический калькулятор упрощает вычисления и экономит время на выполнение ваших заданий или длительные вычисления по математике.

Что такое объем сферы?

Сфера — это множество точек в пространстве, расположенных на заданном расстоянии r от центра.

Объем — это пространство, занимаемое любым трехмерным телом. Объем измеряется в кубических единицах, таких как дюйм³, фут³, см³, м³ и т. д. Перед расчетом объема убедитесь, что все измерения должны быть в одних и тех же единицах.

Калькулятор объема конуса также можно найти на нашем портале.

Что такое Калькулятор объема сферы? 93$$

Преобразовав приведенную выше формулу, вы можете найти радиус:

$$r\;=\;\sqrt{\frac{3v}{4π}}$$

, где v объем шара.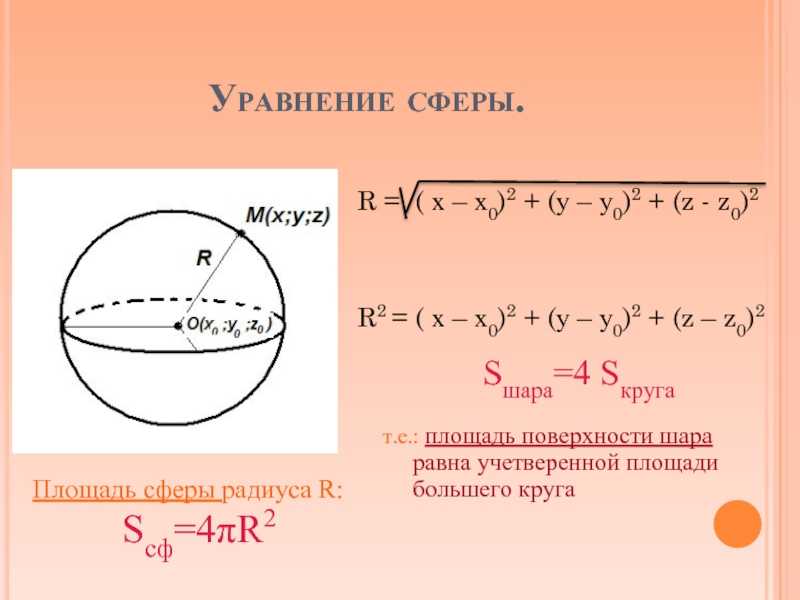

Поскольку все эти формулы разделены, может потребоваться время для их компиляции и поиска правильного ответа. Этот калькулятор площади поверхности сферы составляет эту формулу и дает ответ, решая уравнение с заданными значениями в формуле. Это передовая технология, которая использует фактическое значение числа пи и дает ответ.

Как пользоваться калькулятором объема сферы?

Калькулятор объема сферы прост и удобен в использовании. Просто выполните следующие шаги, чтобы рассчитать объем и окружность сферы.

Сначала вы должны ввести значение радиуса, затем есть кнопка с вкладкой вниз, где вы должны ввести единицу измерения радиуса. Вы увидите три варианта:

• Шаг №1: Введите значение радиуса.
• Шаг #2: Выберите значение радиуса в сантиметрах, метрах или миллиметрах.
• Шаг №3: Нажмите кнопку «РАССЧИТАТЬ».

После того, как вы нажмете кнопку «РАССЧИТАТЬ», калькулятор объема сферы немедленно рассчитает объем сферы и окружность.

Калькулятор разницы между длиной окружности сферы и вычислением объема сферы

Длина окружности сферы или сферы в 6,2832 раза больше радиуса. Окружность круга или сферы в 3,1416 раз больше диаметра.

Итак, между ними есть разница, и обе работают с разной функциональностью. Таким образом, чтобы ваша работа узнать из формулы, чтобы найти окружность сферы, которая является:

$$C\;=\;2πr$$

или

Используйте онлайн-калькулятор окружности для расчета окружности.

Что нужно помнить

• Площадь поверхности сферы = 4πr 2
• Объем сферы = 4/3 πr 3
• Вам нужно знать только радиус, чтобы рассчитать как объем, так и площадь сферы.
• Ответы на вопросы о площади поверхности всегда должны быть в квадратных единицах
• Ответы на задачи с объемом всегда должны быть в кубических единицах

Мы надеемся, что наш калькулятор объема сфер вам удался.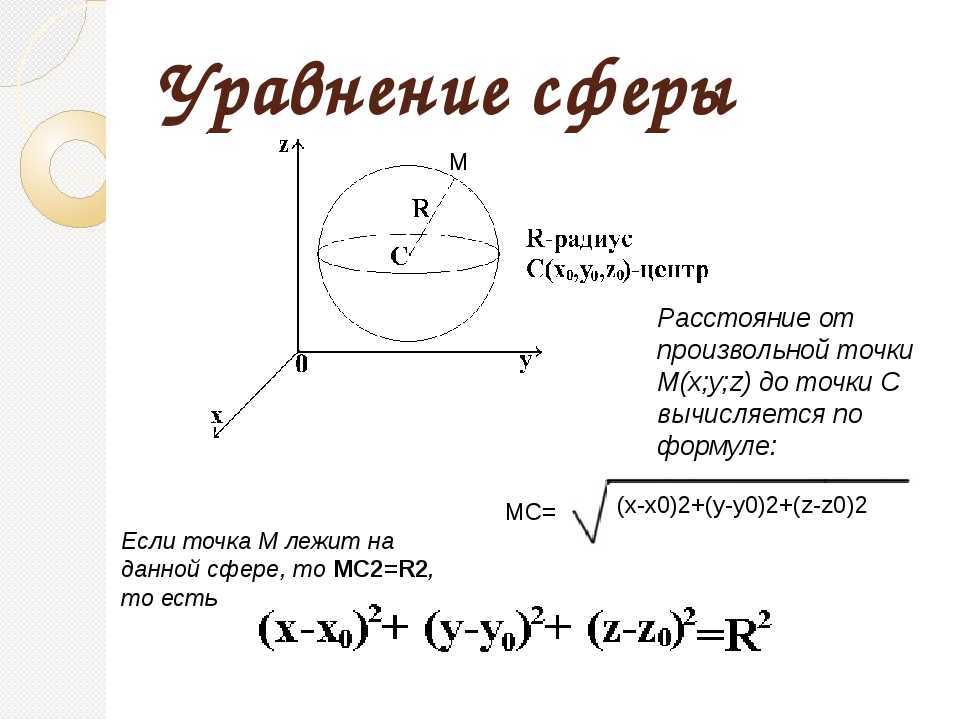

Внешние ресурсы:

• Как рассчитать объем сферы?
• Объем сферы в пересчете на диаметр.
• Формула объема сферы, примеры и приложения.
• Объем сферы с диаметром.

Понятие объема геометрических фигур

Определение 1

Объем геометрической фигуры – это количественная характеристика пространства, занимаемого телом или веществом, определяемая его формой и линейными размерами.

Представьте себе два сосуда: один в форме куба, а другой произвольной формы, до краев наполненный жидкостью. Предположим, что на наполнение первого сосуда ушло m кг жидкости, а на наполнение второго сосуда — n кг жидкости. Таким образом, второй сосуд в n/m раз больше первого. Величина, показывающая, во сколько раз второй сосуд больше первого, называется объемом второго сосуда, если первый сосуд является единицей измерения.

Из этого определения следуют следующие свойства:

Следствие 1

Поскольку для заполнения каждого сосуда требуется определенное количество жидкости, каждый сосуд имеет определенный положительный объем.

Следствие 2

Для заполнения одинаковых сосудов требуется одинаковое количество жидкости, поэтому равные сосуды имеют одинаковый объем.

Следствие 3

Если данный сосуд разделен на две части, то количество жидкости, необходимое для заполнения всего сосуда, состоит из количества жидкости, необходимого для заполнения частей. Следовательно, объем всего сосуда равен сумме объемов его частей.

Площади сферы и ее частей. Объемы шара и его частей

В следующей таблице приведены формулы для расчета объема сферы и объемов ее частей, а также площади сферы и площадей ее частей.

Фигура	Рисунок	Формула	Описание
Прохладный		S = 4πr2, где r — радиус сферы.	Диапазон пуль
Мяч	где r — радиус шара.	Объем мяча
Сферический ремень		S = 2пр, где r — радиус сферы, h – высота сферического пояса. Площадь сферического пояса не зависит от радиусов r1 и r2 !	Площадь сферического пояса
Мяч команда	где r1, r2 — радиусы оснований сферического слоя, h – высота сферического слоя.	Объем сферического слоя
Сферический сегмент		S = 2пр, где r — радиус сферы, h – высота сферического сегмента.	Площадь сферического сегмента
Шаровой сегмент	где r — радиус шара, h – высота сферического сегмента.	Объем сферического сегмента
Сектор мяча		где r — радиус шара, h — высота сферического сектора.	Объем сферического сектора

Прохладный

Диапазон мяча: S = 4πr2, где r — радиус сферы.

Мяч

Объем мяча: где r — радиус шара.

Сферический ремень

Площадь сферического пояса: S = 2пр, где r — радиус сферы, h – высота сферического пояса. Площадь сферического пояса не зависит от радиусов r1 и r2 !

Мяч команда

Объем шаровой кровати: где r1, r2 — радиусы оснований сферического слоя, h – высота сферического слоя.

Сферический сегмент

Площадь сферического сегмента: S = 2пр, где r — радиус сферы, h – высота сферического сегмента.

Шаровой сегмент

Объем шарового сегмента: где r — радиус шара, h – высота сферического сегмента.

Сектор мяча

Объем сектора сферы: где r — радиус шара, h — высота сферического сектора.

Объем сферы – определение, формула, вывод, примеры

Объем сферы – введение

Вы когда-нибудь задумывались: «Я могу нарисовать круг, но не могу нарисовать сферу? Почему?» Это связано с тем, что круг является двухмерной фигурой и не имеет объема, тогда как сфера представляет собой трехмерную форму без краев и вершин. Это означает, что его точки лежат в пространстве. Следовательно, вы не можете его нарисовать. По этой причине мы всегда находим объем сферы, чтобы рассчитать занимаемое ею пространство.

Прокрутите вперед, чтобы узнать о формуле объема сферы, выводе формулы объема сферы, некоторых решенных примерах, фактах и ​​многом другом.

Родственные игры

Каков объем шара?

Хотите знать, как мы можем найти объем сферы? Подождите, мы доберемся до этого, но сначала поймите, что означает объем сферы. Объем сферы является мерой трехмерного пространства, занимаемого сферой. Это зависит от радиуса сферы, который составляет половину диаметра (самая длинная линия внутри сферы, проходящая через центр сферы). 93)$

Интересные факты о сферах

Как насчет некоторых забавных и интересных фактов о сфере? Давайте взглянем!

1. Сфера симметричная и круглая. У него нет граней, углов или ребер.
2. Шары, шарики и даже Земля имеют форму сфер.
3. Полусфера — это точная половина сферы.
4. Все точки поверхности сферы находятся на одинаковом расстоянии «r» от центра.
5. Сфера появляется в природе, когда поверхность хочет быть как можно меньше. Например, если надуть воздушный шар, он естественным образом образует шар!

Заключение

Необходимость определения объема шара может возникнуть в самых разных ситуациях: от абстрактных школьных задач до научных изысканий и производственных вопросов. Для решения вопросов любой сложности используйте наш онлайн-калькулятор, который мгновенно представит вам точный результат и необходимые математические выкладки.

Шар и сфера — это прежде всего геометрические фигуры, и если шар — это геометрическое тело, то сфера — это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.

Впоследствии когда было открыто, что Земля — это шар, а небо — небесная сфера, получило развитие новое увлекательное направление в геометрии — геометрия на сфере или сферическая геометрия. Для того, чтобы рассуждать о размере и объеме шара, нужно сначала дать ему определение.