Площадь поверхности и объем
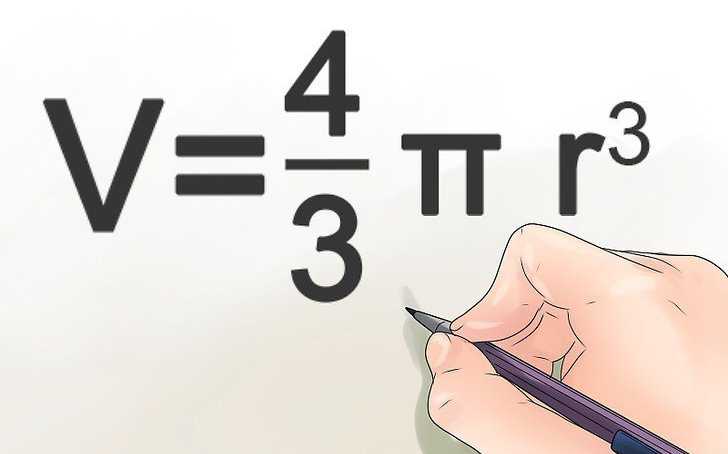
Рассматривая вопрос, как находить объем шара, помимо этой величины, следует привести формулу для его площади, поскольку оба выражения можно связать друг с другом, как будет показано ниже.
Итак, чтобы вычислить объем шара, следует применить одну из следующих двух формул:
- V = 4/3 *pi * R3;
- V = 67/16 * R3.
Здесь R — радиус фигуры. Первая из приведенных формул является точной, однако, чтобы воспользоваться этим преимуществом, необходимо использовать соответствующее число знаков после запятой для числа pi. Второе выражение дает вполне хороший результат, отличаясь от первого всего на 0,03 %. Для ряда практических задач этой точности более чем достаточно.
Равна этой величине для сферы, то есть выражается формулой S = 4 * pi * R2. Если отсюда выразить радиус, а затем подставить его в первую формулу для объема, тогда получим: R = √ (S / (4 * pi)) = > V = S / 3 * √ (S / (4 * pi)).
Таким образом, мы рассмотрели вопросы, как найти объем шара через радиус и через площадь его поверхности. Эти выражения можно с успехом применять на практике. Далее в статье приведем пример их использования.
Определение основных величин

- Диаметр (D) – это отрезок, который соединяет две точки на поверхности шара и проходит через его центр (то есть это наибольшее расстояние между противоположными точками, лежащими на поверхности шара). Диаметр равен удвоенному радиусу.
- Длина окружности (С) представляет собой длину окружности большого круга, то есть круга, который образует секущая плоскость, проходящая через центр шара.
- Объем (V) – это значение трехмерного пространства, занимаемого шаром.
- Площадь поверхности (А) – это значение двумерного (плоского) пространства, ограниченного поверхностью шара.
- Пи (π) – это постоянная, которая равна отношению длины окружности к ее диаметру. Первыми десятью цифрами этой постоянной являются 3,141592653, но зачастую число Пи округляется до 3,14.

- D = 2г. Как и в случае круга , диаметр шара в два раза больше его радиуса.
- C = πD = 2πr. Как и в случае круга , длина окружности шара равна произведению π на диаметр шара. Так как диаметр вдвое больше радиуса, то длина окружности шара равна удвоенному произведению π на радиус шара.
- V = (4/3)πr 3 . Объем шара равен произведению 4/3 на π и на радиус в кубе.
- А = 4πr 2 . Площадь поверхности шара равна учетверенному произведению π на радиус в квадрате. Так как площадь круга равна πr 2 , то площадь поверхности шара в четыре раза больше площади круга, который образует секущая плоскость, проходящая через центр шара.
Важные измерения
Радиус (обозначается r) — единственное необходимое измерение. Это расстояние от любой точки на поверхности сферы до её центра. Самый длинный отрезок, равный двум r, называется диаметром (d). Земля называется сфероидом, потому что она очень близка к шару, но не идеально круглая. Она немного вытянута на северном и южном полюсах.

Впервые вычислить площадь (S) поверхности шара удалось Архимеду. Именно он установил, что для того, чтобы найти S любого трёхмерного объекта, необходимо измерить его радиус. Для сферы получилась следующая формула: S = 4 * π * r ². Для того чтобы понять, как это работает, следует рассмотреть пример. Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:
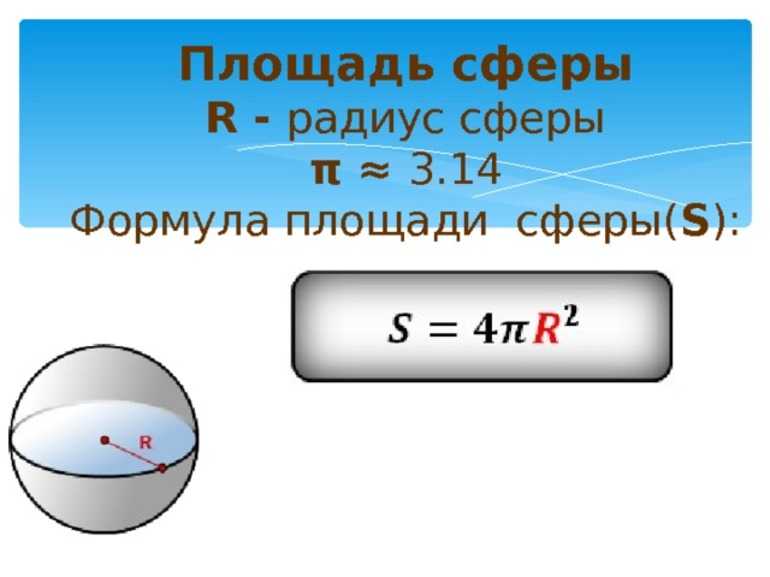
- S = 4 * 3,14 * 10²;
- S мяча равна ≈ 1256 см².
Таким образом, можно найти площадь сферы через её радиус по формуле, полученной ещё в античности. Ещё одна важная характеристика — это объём (V) фигуры. Он вычисляется следующим образом: V = (4/3) * π * r³. Если придерживаться условий задачи, то V мяча = (4/3) * 3,14 * 10³ равен ≈ 4187 см ³. Сейчас можно избежать длительных расчётов, если нужно узнать площадь сферы, онлайн-калькуляторы — сервисы, которые очень в этом помогают.
Надо сказать, что внутренний конус может иметь основание с нулевым радиусом. Формула, по которой определяют площадь сектора, следующая: S = 2 * π * r * h, где h — высота. К слову, эта же формула применима, если необходимо найти S части шара, отрезанной плоскостью, то есть полусферы. Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
Что такое шар?
В стереометрии есть большой раздел, который называется фигуры вращения. Об этом редко говорят в школе, но плоские фигуры можно вращать вокруг какой-либо оси или точки. Так получаются объемные фигуры.
Например, цилиндр образован вращением прямоугольника или квадрата. Поэтому, если рассечь цилиндр плоскостью, то сечение примет форму того самого квадрата или прямоугольника, который вращали, чтобы получить фигуру.
Так же и шар образован вращением. Как не трудно догадаться, основной для шара послужил круг. Причем сразу стоит сказать, что именно круг, а не окружность.
Следует понимать, что круг и окружность разные фигуры. Так окружность представляет собой набор точек равноудаленных от центра. Переводя на более простой язык окружность – это сама линия и центр окружности. А круг включает в себя и все внутреннее пространство. У окружности не может быть площади.
То есть, шар имеет какое-то внутренне заполненное пространство. Интересно, что сфера так же имеет пространство внутри, только условно полое.
Как найти радиус сферы
Все ресурсы по геометрии среднего уровня
8 диагностических тестов 250 практических тестов Вопрос дня Карточки Learn by Concept
Intermediate Geometry Help » Твердая геометрия » Сферы » Как найти радиус сферы
Если объем сферы равен , какова приблизительная длина ее диаметра?
Возможные ответы:
Правильный ответ:
Объяснение:
Правильный ответ: 6,12 фута.

Подставьте значение в уравнение так, чтобы 0002 Затем разделите обе части на , чтобы получить
Затем возьмите корень 3 rd с обеих сторон, чтобы получить 3,06 фута для радиуса. Наконец, вы должны умножить на 2 с обеих сторон, чтобы получить диаметр. Таким образом,
Сообщить об ошибке
Объем сферы равен . Каков его радиус?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула объема сферы:
Единственная данная информация в задаче – это окончательный объем сферы. Если объем равен , формулу объема можно использовать для расчета радиуса сферы.
В этом случае радиус — единственная неизвестная переменная, для которой нужно найти решение.
Сообщить об ошибке
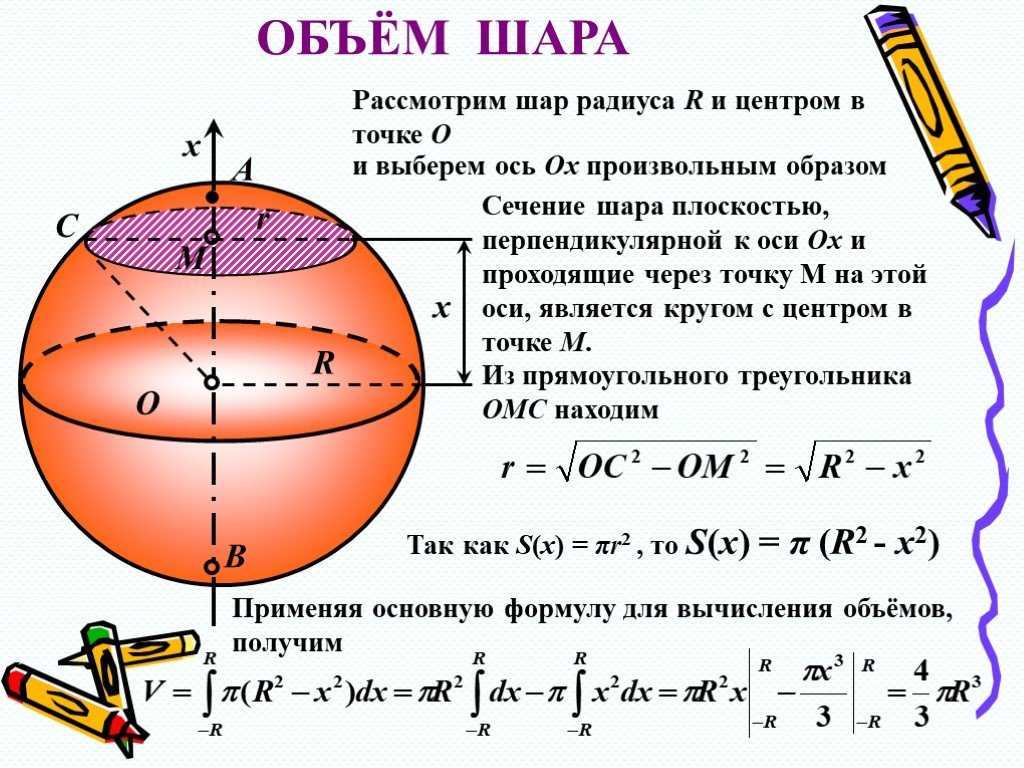
Площадь сферы составляет .
Возможные ответы:
Правильный ответ:
Объяснение:
Единственная предоставленная информация — это площадь .
К этой задаче можно подойти «назад», где формула площади для сферы может быть использована для определения радиуса. Это возможно, потому что формула для площади , где (радиус) — это то, что мы ищем. После замены площади на , цель состоит в том, чтобы найти , получив ее саму по одну сторону от знака равенства.
Сообщить об ошибке
Если объем сферы равен , каков точный радиус сферы?
Возможные ответы:
Правильный ответ:
Объяснение:
Напишите формулу объема сферы:
Подставьте данный объем и найдите радиус .
Начните с умножения каждой части уравнения на :
Теперь разделите каждую часть уравнения на :
Наконец, извлеките кубический корень из каждой части уравнения:
Ошибка
Учитывая объем сферы есть, каков радиус?
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение объема сферы:
, где – длина радиуса сферы.
Подставьте заданный объем и решите, чтобы рассчитать радиус сферы:
Сообщить об ошибке
Если объем сферы равен , каков радиус сферы?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула объема сферы:
, где – радиус сферы.
Объем шара через радиус
{V= dfrac{4}{3}pi r^3}
Формула для нахождения объема шара через радиус: {V= dfrac{4}{3}pi r^3}, где r — радиус шара.
Шар, сфера и их части
Введем следующие определения, связанные с шаром, сферой и их частями.
Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).
Рис.1
Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание. Радиусом сферы (радиусом шара) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы (радиусом шара).
Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Определение 4. Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Рис.2
Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.
Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя.
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).
Рис.3
Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.
Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента.
Рис.4
По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).
Рис.5
Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).
Рис.6
Высотой шарового сектора называют высоту его сферического сегмента.
Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы.
Советуем посмотреть:
Предмет стереометрии
Параллельность и перпендикулярность прямых и плоскостей в пространстве
Многогранник
Призма
Параллелепипед
Объём тела
Свойства прямоугольного параллелепипеда
Пирамида
Цилиндр
Конус
Многогранники
Резюме
И шар, и сфера являются абстрактными геометрическими объектами (геометрическими фигурами), задаваемыми через некоторое геометрическое место точек пространства — например, с помощью понятия центра шара/сферы и радиуса шара/сферы. Однако только шар является полноценным геометрическим телом, поскольку включает в себя не только описание ограничивающей его поверхности, но и всей той части пространства, что в себя эта поверхность заключает. С такой точки зрения сфера — лишь внешняя абстрактная граница (поверхность) задаваемого в пространстве шара.
Символ шара-глобальность шара Земли. Символ будущего, он отличается от креста тем, что последний олицетворяет собой страдание и человеческую смерть. В Древнем Египте впервые пришли к заключению, что земля шарообразна. Это предположение послужило основой для многочисленных размышлений о бессмертии земли и возможности бессмертия населяющих ее живых организмах.
Данная точка (О) называется центром сферы. Любой отрезок, соединяющий центр и какую-нибудь точку сферы, называется радиусом сферы (R-радиус сферы). Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. Очевидно, что диаметр сферы равен 2R.
Определение шара Шар – это тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки (или фигура, ограниченная сферой). Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Шар
Плоскость,проходящая через центр шара,называется диаметральной плоскостью.Плоскость,проходящая через центр шара,называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом,а сечение сферы — большой окружностью.Сечение шара диаметральной плоскостью называется большим кругом,а сечение сферы — большой окружностью.
X²+y²=R²-d² Если d>R, то сфера и плоскость не имеют общих точек.
R, то сфера и плоскость не имеют общих точек.»>
R, то сфера и плоскость не имеют общих точек.»>
R, то сфера и плоскость не имеют общих точек.» title=»x²+y²=R²-d² Если d>R, то сфера и плоскость не имеют общих точек.»>
title=»x²+y²=R²-d² Если d>R, то сфера и плоскость не имеют общих точек.»>
Касательная плоскость к сфере касательной плоскостью к сфереПлоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, точкой касания А плоскости и сферы.а их общая точка называется точкой касания А плоскости и сферы.
Теорема: Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости. Доказательство: Рассмотрим плоскость α, касающуюся сферы с центром О в точке А. Докажем, что ОА перпендикулярен α. Предположим, что это не так. Тогда радиус ОА является наклонной к плоскости α, и, следовательно расстояние от центра сферы до плоскости меньше радиуса сферы. Поэтому сфера и плоскость пересекаются по окружности. Это противоречит тому, что-касательная, т.е. сфера и плоскость имеют только одну общую точку. Полученное противоречие доказывает, что ОА перпендикулярен α.
Определение.
Сфераповерхность шарацентром сферы
Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение.
Шарцентром шара
Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение.Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение.Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Формула.Объём шара:
| V = | 4 | π R 3 = |
1 | π D 3 |
| 3 | 6 |
Формула.Площадь поверхности сферы через радиус или диаметр:
S = 4π
R 2 = π
D 2
Как найти радиус сферы
Все ресурсы по промежуточной геометрии
Intermediate Geometry Help »
Твердая геометрия »
Сферы »
Как найти радиус сферы
Если объем сферы равен , какова приблизительная длина ее диаметра?
Возможные ответы:
Правильный ответ:
Объяснение:
Правильный ответ составляет 6,12 фута
Подключите значение в уравнение, чтобы
Умножьте обе стороны на 3 на
, затем разделите обе стороны на
.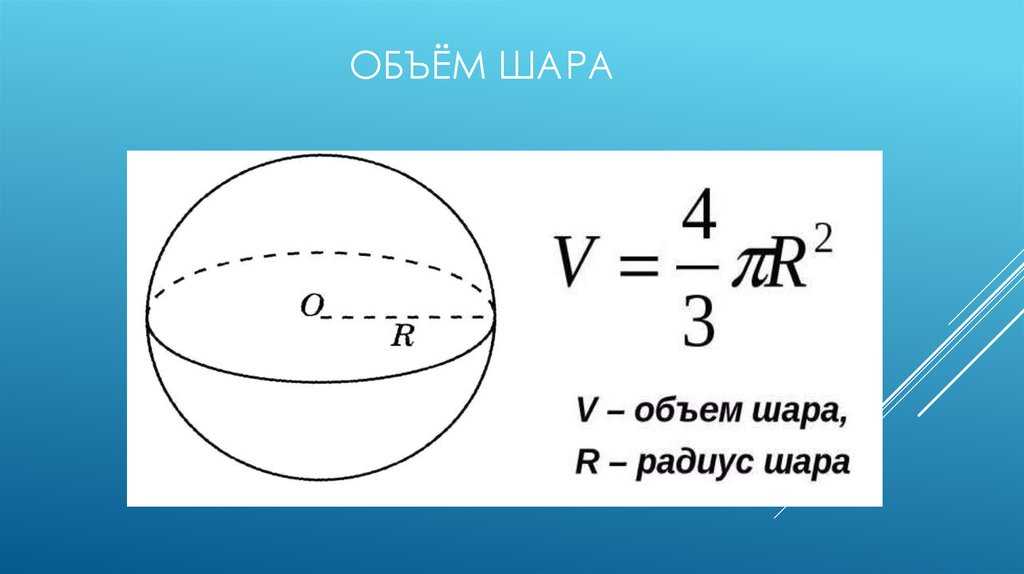
rd
Сообщить об ошибке
Объем сферы . Каков его радиус?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула объема сферы:
Единственная данная информация в задаче – это окончательный объем сферы. Если объем равен , формулу объема можно использовать для расчета радиуса сферы.
В этом случае , радиус, является единственной неизвестной переменной, для которой необходимо найти решение.
Сообщить об ошибке
Площадь сферы составляет . Каков его радиус?
Возможные ответы:
Правильный ответ:
Объяснение:
Единственная предоставленная информация — это площадь .
К этой задаче можно подойти «назад», где формула площади для сферы может быть использована для определения радиуса. Это возможно, потому что формула для площади , где (радиус) — это то, что мы ищем. После замены площади на , цель состоит в том, чтобы найти , получив ее саму по одну сторону от знака равенства.
Сообщить об ошибке
Если объем сферы равен , каков точный радиус сферы?
Возможные ответы:
Правильный ответ:
Объяснение:
Напишите формулу объема сферы:
Подставьте данный объем и найдите радиус .
Начните с умножения каждой части уравнения на :
Теперь разделите каждую часть уравнения на :
Наконец, извлеките кубический корень из каждой части уравнения:
Сообщите об ошибке есть, каков радиус?
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение объема сферы:
, где – длина радиуса сферы.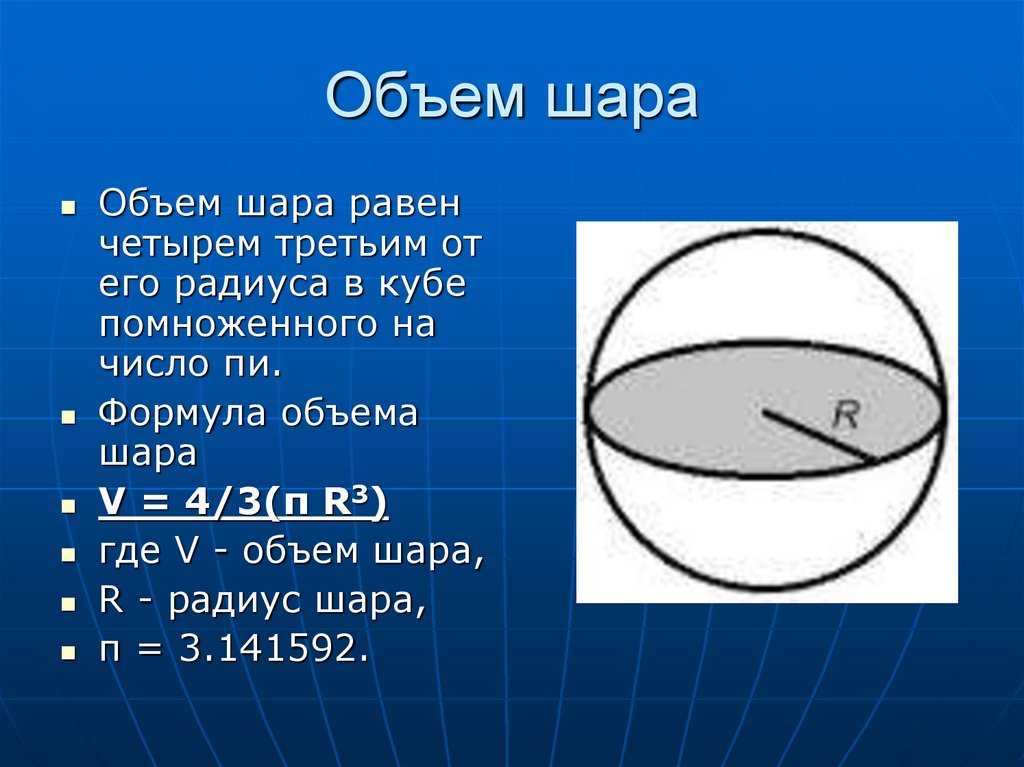
Подставьте заданный объем и решите для , чтобы вычислить радиус сферы:
Сообщить об ошибке
Если объем сферы равен , каков радиус сферы?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула объема сферы:
, где – радиус сферы.
Подставьте объем и найдите радиус сферы:
Сообщить об ошибке
Найдите радиус сферы, если площадь поверхности равна .
Возможные ответы:
Правильный ответ:
Объяснение:
Формула площади поверхности сферы:
Подставьте заданное значение площади поверхности сферы в уравнение и найдите радиус:
Сообщить об ошибке
Найдите радиус сферы, если площадь ее поверхности равна .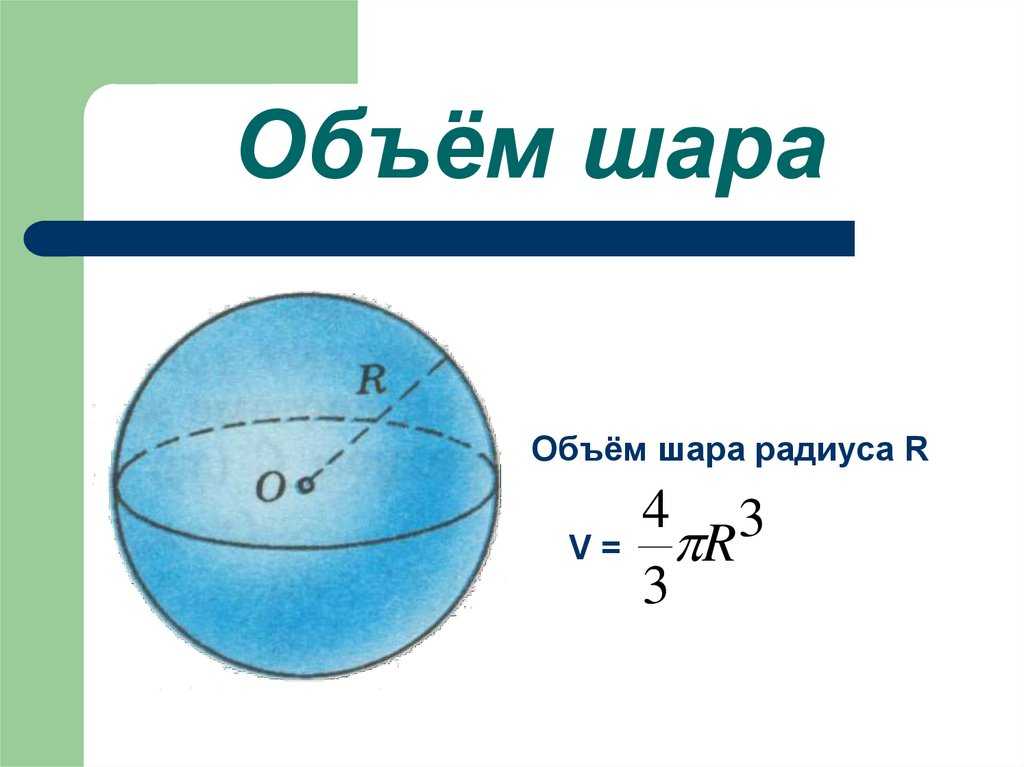
Возможные ответы:
Правильный ответ:
Формула площади поверхности для сферы:
, где – радиус сферы.
Подставьте заданное значение площади сферы в уравнение и решите , чтобы найти радиус:
Сообщить об ошибке
Уведомление об авторских правах
Радиус шара – формула
4.
Средняя оценка: 4.6
Всего получено оценок: 166.
4.6
Средняя оценка: 4.6
Всего получено оценок: 166.
Радиус шара это простейшая величина в стереометрии, но при этом найти его получится только через объем. Для того чтобы разобраться в вопросе, выведем формулу радиуса шара и расскажем, как же правильно вычислить радиус.
Что такое шар?
В стереометрии есть большой раздел, который называется фигуры вращения. Об этом редко говорят в школе, но плоские фигуры можно вращать вокруг какой-либо оси или точки. Так получаются объемные фигуры.
Стереометрия это наука о фигурах в пространстве. Простейшими единицами стереометрии является точка, прямая и плоскость.
Например, цилиндр образован вращением прямоугольника или квадрата. Поэтому, если рассечь цилиндр плоскостью, то сечение примет форму того самого квадрата или прямоугольника, который вращали, чтобы получить фигуру.
Так же и шар образован вращением. Как не трудно догадаться, основной для шара послужил круг.
Что мы узнали?
Мы поговорили о том, что такое шар. Привели все формулы шара. Вспомнили, что такое число пи. Вывели формулу радиуса шара.
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Примеры из жизни
Пушечные ядра
Допустим, вы хотите узнать, сколько чугуна необходимо для отливки пушечного ядра шестифутового калибра. Вы знаете, что диаметр такого ядра составляет 9,6 сантиметров. Введите это число в ячейку калькулятора «Диаметр», и вы получите ответ в виде
Таким образом, для выплавки пушечного ядра заданного калибра вам понадобится 463 кубических сантиметров или 0,463 литра чугуна.
Воздушные шары
Пусть вам любопытно, сколько воздуха необходимо для накачки воздушного шара идеальной сферической формы. Вы знаете, что радиус выбранного шарика составляет 10 см. Вбейте это значение в ячейку калькулятора «Радиус» и вы получите результат
Это означает, что для накачки одного такого шара вам понадобится 4188 кубических сантиметров или 4,18 литров воздуха.
Видео с вопросами: Нахождение радиуса сферы по ее объему
Стенограмма видео
Найдите радиус сферы, объем которой
девять на два 𝜋 кубических сантиметра.
В этой задаче нам дали
объем сферы и попросили работать в обратном направлении, чтобы определить ее радиус.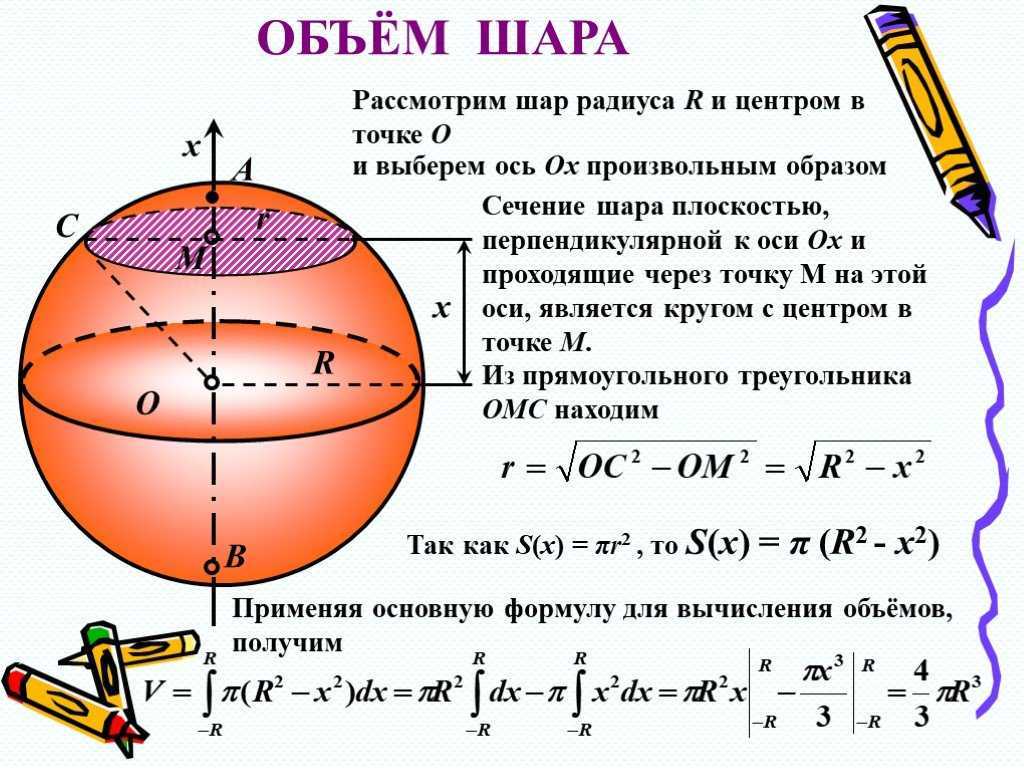
Теперь, когда нам дали объем, и мы
зная общую формулу для ее решения, мы можем установить эти два значения или выражения
равны друг другу, чтобы получить уравнение. У нас четыре трети 𝜋𝑟 в кубе равны
девять больше двух 𝜋. А для определения радиуса
сферы, нам просто нужно решить это уравнение.
Во-первых, мы замечаем, что есть коэффициент
𝜋 с каждой стороны уравнения. Так что мы можем отменить это. Или мы можем думать об этом как о разделении
на 𝜋, чтобы четыре трети 𝑟 в кубе равнялись девяти на два. Далее нам нужно разделить каждую сторону
уравнение на четыре трети, чтобы оставить 𝑟 в кубе в левой части.
Напомним, что деление на дробь
эквивалентно умножению на обратную часть этой дроби. Итак, чтобы разделить на четыре трети, мы можем
умножьте каждую часть уравнения на три четверти.
Сейчас мы помним, что в
Чтобы найти кубический корень дроби, мы можем найти кубический корень числителя по
кубический корень из знаменателя. Итак, мы имеем, что 𝑟 равно кубическому корню.
числа 27 больше кубического корня из восьми. И это оба целые значения. Кубический корень из 27 равен трем, а
кубический корень из восьми равен двум. Отсюда получаем, что радиус этой сферы
три на два или 1,5. А так как единицы объема были
кубические сантиметры, единицами измерения радиуса будут сантиметры.
Формулы для вычисления радиуса

Например, дан шар с диаметром 16 см. Радиус этого шара: r = 16/2 = 8 см. Если диаметр равен 42 см, то радиус равен 21 см (42/2=21).

- Например, дан шар с длиной окружности 20 см. Радиус этого шара: r = 20/2π = 3,183 см.
- Такая же формула используется при вычислении радиуса и длины окружности круга.
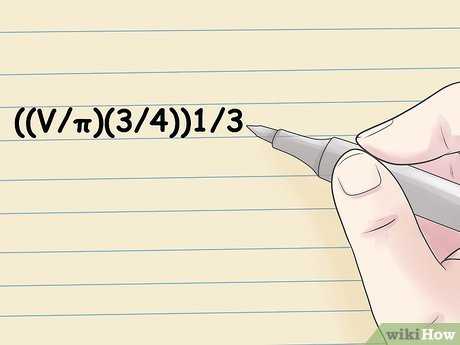
- Например, дан шар с объемом 100 см 3 . Радиус этого шара вычисляется так:
- ((V/π)(3/4)) 1/3 = r
- ((100/π)(3/4)) 1/3 = r
- ((31,83)(3/4)) 1/3 = r
- (23,87) 1/3 = r
- 2,88 см = r
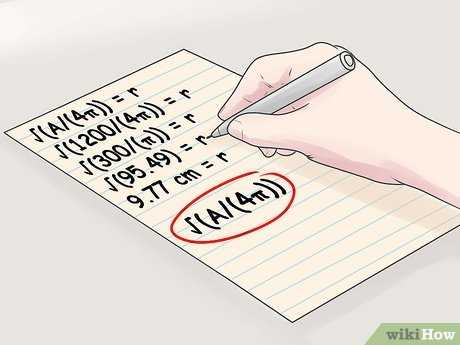
- Например, дан шар с площадью поверхности 1200 см 3 . Радиус этого шара вычисляется так:
- √(A/(4π)) = r
- √(1200/(4π)) = r
- √(300/(π)) = r
- √(95,49) = r
- 9,77 см = r
Заключение
Необходимость определения объема шара может возникнуть в самых разных ситуациях: от абстрактных школьных задач до научных изысканий и производственных вопросов. Для решения вопросов любой сложности используйте наш онлайн-калькулятор, который мгновенно представит вам точный результат и необходимые математические выкладки.
Шар и сфера — это прежде всего геометрические фигуры, и если шар — это геометрическое тело, то сфера — это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.
Впоследствии когда было открыто, что Земля — это шар, а небо — небесная сфера, получило развитие новое увлекательное направление в геометрии — геометрия на сфере или сферическая геометрия. Для того, чтобы рассуждать о размере и объеме шара, нужно сначала дать ему определение.