Арксинус и арккосинус − теория, примеры и решения
Функция арксинус и ее график
Как известно, функция синус определена в интервале и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.1) (подробнее о функции синус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.
Однако, функцию синус можно разделить на интервалы, где она монотонна. Эти интервалы:
По теореме об обратной функции, на каждом из указанных отрезков функция sin x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arcsin y. Поменяв местами x и y, получим:
Функция (1) − это функция, обратная к функции
График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.2).
Свойства функции арксинус.
- Область определения функции: .
- Область значений функции: .
- Функция является нечетной: .
- Функция возрастает.
- Функция непрерывна.
Решим тригонометрическое уравнение
При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором sin x>1 (см. график функции синус (Рис.1). При |a|≤1, в отрезке (дуга DAB) уравнение (2) имеет одно решение (см. Рис.3):
В отрезке (дуга DCB) функция синус убывает и принимает значения от 1 до −1. Следовательно в этом отрезке уравнение (2) также имеет решение:
Действительно:
А из
следует
т.е.
Таким образом уравнение (3) имеет два решения в отрезке :
которые совпадают при |a|=1.
Поскольку функция синус периодичная с основным периодом 2π, имеем
Тогда получим решение (2) в виде
Решения (3) и (4) удобно представить одним уравнением:
Действительно. При четных k (k=2n) из уравнения (5) получают все решения, представленные уравнением (3), а при нечетных k (k=2n+1) − все решения, представленные уравнением (4).
При a=1, arcsin a и π−arcsin a совпадают (т.к. ), следовательно решение уравнения sin t=1 имеет вид:
При |a|=−1, из (3) и (4) следует:
Но поворот эквивалентно повороту . То есть уравнения (6) и (7) эквивалентны. Тогда решение уравнения sin t=−1 запишем в виде:
При |a|=0, из (3) и (4) имеем следующее решение уравнения sin t=0:
Пример 1. Решить тригонометрическое уравнение:
Решение. Воспользуемся формулой (5):
т.е.
Пример 2. Решить тригонометрическое уравнение:
Решение. Воспользуемся формулой (5):
т.е.
Функция арккосинус и ее график
Как известно, функция косинус определена в интервале и не является монотонной функцией (Рис.4) (подробнее о функции косинус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.
Однако, функцию косинус можно разделить на интервалы, где она монотонна. Эти интервалы:
По теореме об обратной функции, на каждом из указанных отрезков функция cos x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arccos y. Поменяв местами x и y, получим:
Функция (8) − это функция, обратная к функции
График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).
Свойства функции арксинус.
- Область определения функции: .
- Область значений функции: .
- Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
- Функция убывает.
- Функция непрерывна.
Решим тригонометрическое уравнение
При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором cos x>1 (см. график функции косинус (Рис.4). При |a|≤1, в отрезке [0; π] (дуга ABC) уравнение (9) имеет одно решение t1=arccos a. В отрезке [−π; 0] (дуга CDA) уравнение (9) имеет одно решение t2=−arccos a(см. Рис.6):
Таким образом, в интервале [−π; π] уравнение (9) имеет два решения y=± arccos a, которые совпадают при a=1.
Поскольку функция косинус периодичная с основным периодом 2π:
то общее решение (9) имеет следующий вид:
При a=1, числа arccos a и −arccos a совпадают (они равны нулю), тогда решение уравнения cos t=1 можно записать так:
При a=−1, имеем cos t=−1,
При a=0, имеем cos t=0,
Решение тригонометрического уравнения cos t=0 можно записать одним уравнением:
Пример 1. Решить тригонометрическое уравнение:
Решение. Воcпользуемся формулой (10):
Так как , то
Пример 2. Решить следующее тригонометрическое уравнение:
Решение. Используя формулу (10), имеем
Так как (), то
Пример 3. Решить следующее тригонометрическое уравнение:
Решение. Используя формулу (10), имеем
С помощью онлайн калькулятора вычисляем : . Тогда решение можно записать так:
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
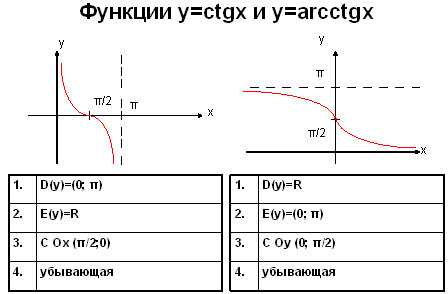
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 – 1, рис. 2 – 4.
Inverse properties
Generally, functions and their inverses exhibit the relationship
f(f-1(x)) = x and f-1(f(x)) = x
given that x is in the domain of the function. The same is true of sin(x) and arcsin(x) within their respective restricted domains:
sin(arcsin(x)) = x, for all x in
and
arcsin(sin(x)) = x, for all x in [, ]
These properties allow us to evaluate the composition of trigonometric functions.
Composition of arcsine and sine
If x is within the domain, evaluating a composition of arcsine and sine is relatively simple.
Examples:
1.
2.
If x is not within the domain, we need to determine the reference angle as well as the relevant quadrant. Given arcsin(sin() ), we cannot evaluate this as we did above because x is not within [, ], so the solution cannot be . To evaluate this, we first need to determine sin() before using arcsin:
3.
In the above example, the reference angle is and sin() is . However, is in quadrant III where sin is negative, so sin() = , and the only angle within the domain of arcsin(x) whose sine is is .
Composition of other trigonometric functions
We can also make compositions using all the other trigonometric functions: cosine, tangent, cosecant, secant, and cotangent.
Example:
Find cos(arcsin()).
Since is not one of the ratios for the special angles, we can use a right triangle to find the value of this composition. Given arcsin()=θ, we can find that sin(θ)=. The right triangle below shows θ and the ratio of its opposite side to the triangle’s hypotenuse.
To find cosine, we need to find the adjacent side since cos(θ)=. Let b be the length of the adjacent side. Using the Pythagorean Theorem,
32 + b2 = 52
9 + b2 = 25
b2 = 16
b = 4
We know that arcsin() = θ, so we can rewrite the problem and find cos(θ) by using the triangle we constructed above and the fact that cos(θ)=:
cos(arcsin()) = cos(θ) =
The same process can be used with a variable expression.
Example:
Find tan(arcsin(2x)).
Given arcsin(2x) = θ, we can find that sin(θ) = and construct the following triangle:
To find tangent, we need to find the adjacent side since tan(θ)=. Let b be the length of the adjacent side. Using the Pythagorean theorem,
(2x)2 + b2 = 12
4×2 + b2 = 1
b2 = 1 — 4×2
b =
and
tan(arcsin(2x)) = tan(θ) = , where <x<
Формулы
Формулы суммы и разности
при или
при 0,\,y>0 \;» style=»width:114px;height:18px;vertical-align:-10px;background-position:-638px -553px»> и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-211px -513px»>
при и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-211px -513px»>
при или
при 0,\,y и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-211px -513px»>
при 0 \;» style=»width:108px;height:18px;vertical-align:-10px;background-position:-0px -571px»> и 1″ style=»width:102px;height:22px;vertical-align:-10px;background-position:-211px -513px»>
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
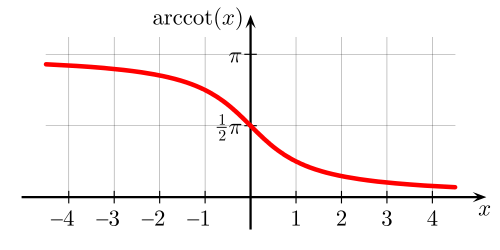
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2.
Соотнести график и форму записи функции.
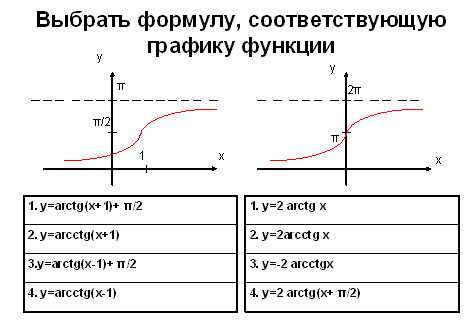
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ:
рис. 1 – 1, рис. 2 – 4.
Решение уравнения sinx = a
Ур-ние cosx = a называют простейшим тригонометрическим уравнением, ведь, ведь для его решения не требуется проводить никаких преобразований. Аналогично простейшими являются ур-ния sinx = a, tgx = a и ctgx = a.
Ситуация с ур-нием sinx = a аналогична ситуации с косинусом. Если число а не принадлежит промежутку , то корней у ур-ния не будет. Если же число а будет принадлежать этому промежутку, то у ур-ния окажется бесконечное число решений.
Рассмотрим случай, когда 0<а< 1. Тогда решениями ур-ния окажутся числа arcsina и π – arcsina:
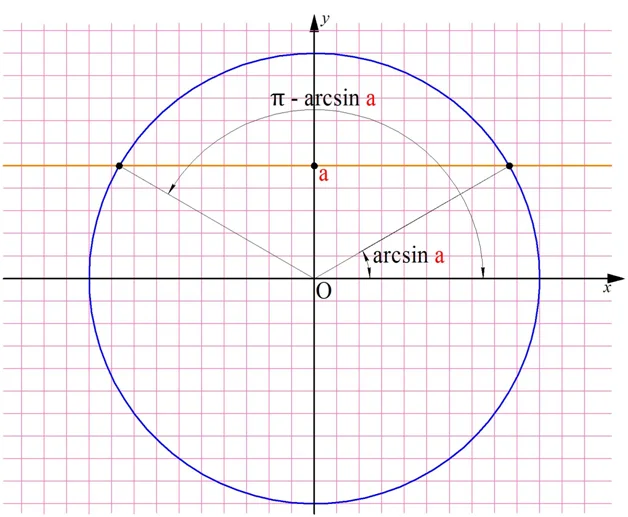
В свою очередь каждое из этих двух решений порождает свою собственную бесконечную серию решений
Однако, как и в случае с косинусом, существует способ записать одной формулой сразу оба этих решения. Для этого перепишем первую серию таким образом:

Действительно, если n окажется четным, то, то выражение (– 1)n,будет равно единице, и мы получим первую серию. Если же n – нечетное число, то, то выражение (– 1)n окажется равным (– 1), и мы получим вторую серию.

Задание. Решите ур-ние

Задание. Запишите корни ур-ния

Теперь будем подставлять в это решение значения n, чтобы найти конкретные значения х. Нас интересуют корни, которые больше π, но меньше 4π, поэтому будем сразу сравнивать полученные результаты с этими числами.
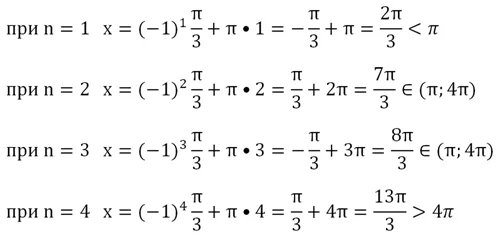
Получили два корня, относящихся к промежутку – это 7π/3 и 8π/3. Нет смысла проверять другие возможные значения n, ведь они будут давать корни, заведомо меньшие 2π/3 или большие 13π/3:
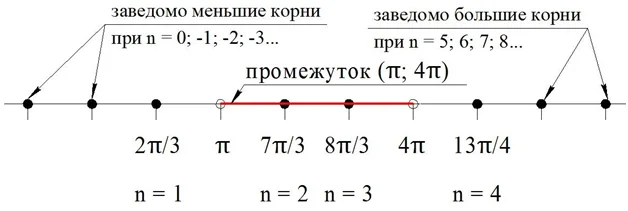
Ответ: 7π/3 и 8π/3.
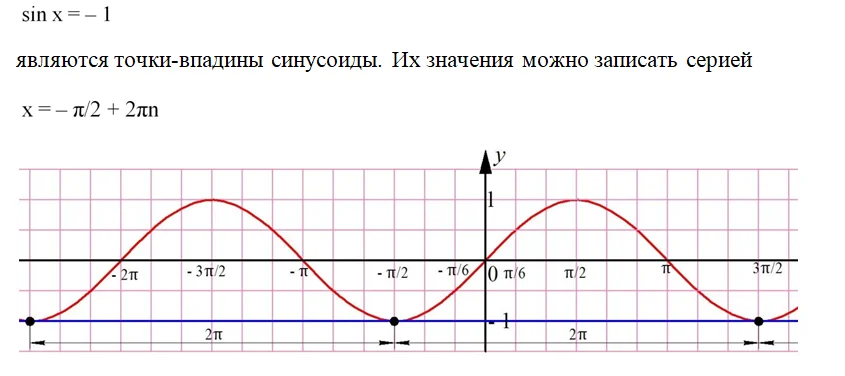
Как и в случае с косинусом, есть несколько частных случаев, когда решение ур-ния записывается проще. Ур-ние

Это видно из графика, где корням ур-ния соответствуют точки пересечения синусоиды с осью Ох:
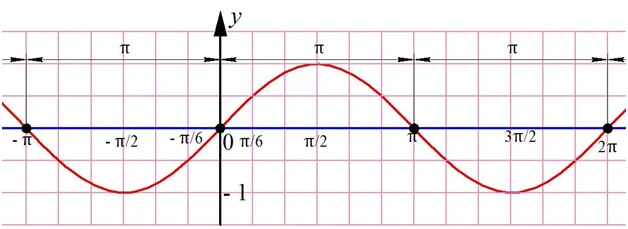
Решениями ур-ния

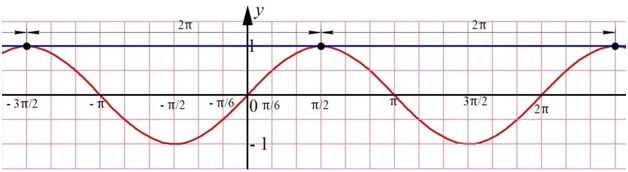
Наконец, решениями ур-ния
Арктангенс и арккотангенс − теория, примеры и решения
Функция арктангенс и ее график
Функция тангенс определена в интервале кроме точек , . и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.1) (подробнее о функции тангенс смотрите на странице Тангенс и котангенс. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.
Однако, функцию тангенс можно разделить на интервалы, где она монотонна. Эти интервалы:
| , , , и т.д. |
По теореме об обратной функции, на каждом из указанных отрезков функция tg x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arctg y. Поменяв местами x и y, получим:
| y=arctg x. | (1) |
Функция (1) − это функция, обратная к функции
| . |
График функции арктангенс можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.2).
Свойства функции арктангенс.
- Область определения функции: .
- Область значений функции: .
- Функция является нечетной: .
- Функция возрастает.
- Функция непрерывна.
Решим тригонометрическое уравнение
В интервале для уравнения (2) существует одно t, для которого tg t=a. Это решение
Следовательно в интервале уравнение (2) имеет один корень. Так как тангенс периодичная функция с основным периодом π, то все корни уравнения (2) отличаются на πn (n∈Z), т.е.
| . | (3) |
Решение уравнения (2) представлен на Рис.3:
Так как tg t − это ординат точки пересечения прямой OMt1 c прямым x=1, то для любого a на линии тангенса есть только одна точка T(1; a). Прямая OTt пересекается с окружностью с радиусом 1 в двух точках: . Но только точка соответствует интервалу , которое соответствует решению .
Пример 1. Решить тригонометрическое уравнение:
| . |
Решение. Воспользуемся формулой (3):
| , |
| . |
Пример 2. Решить тригонометрическое уравнение:
| . |
Решение. Воспользуемся формулой (3):
| . |
Используя онлайн калькулятор получим:
| . |
Функция арккотангенс и ее график
Как известно, функция котангенс определена в интервале кроме точек -2π, —π 0, π, 2π. и не является монотонной функцией (Рис.4) (подробнее о функции котангенс смотрите на странице Тангенс и котангенс. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.
Однако, функцию кокотангенс можно разделить на интервалы, где она монотонна. Эти интервалы:
По теореме об обратной функции, на каждом из указанных интервалов функция ctg x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arcctg y. Поменяв местами x и y, получим:
| y=arcctg x. | (4) |
Функция (4) − это функция, обратная к функции
| . |
График функции арккотангенс можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).
Свойства функции арккотангенс.
- Область определения функции: .
- Область значений функции: .
- Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
- Функция убывает.
- Функция непрерывна.
Решим тригонометрическое уравнение
В интервале (0; π) для уравнения (5) существует одно t, для которого сtg t=a. Это t=arcctg a. Следовательно в интервале (0; π) уравнение (5) имеет один корень. Так как котангенс периодичная функция с основным периодом π, то общее решение уравнения (5) имеет следующий вид:
| (6) |
Решения уравнения (5) можно представить на единичной окружности (Рис.6):
ctg t − это абсцис точки пересечения прямой с прямым y=1. Любому числу a на линии котангенс соответствует только одна точка . Прямая пересекется с единичной окружностью в двух точках . Но только точка соответствует интервалу (0; π), которое соответствует решению .
Пример 1. Решить тригонометрическое уравнение:
| . |
Решение. Воcпользуемся формулой (6):
| . |
Так как в интервале (0; π), то
| . |
Пример 2. Решить следующее тригонометрическое уравнение:
| . |
Решение. Используя формулу (6), имеем
| . |
С помощью онлайн калькулятора вычисляем . Тогда
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x
зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке .
- ОДЗ для arccos — .
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.

Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1.
Укажите функции изображенные на рисунке.
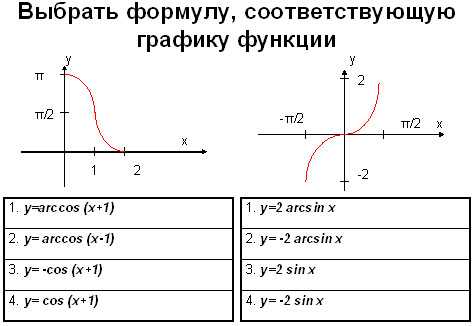
Ответ:
рис. 1 – 4, рис.2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Обратные функции отрицательного аргумента
Применяя указанные выше формулы и свойства тригонометрических функций, получаем формулы обратных функций отрицательного аргумента.
arcsin(-
x)
=
arcsin(-sin arcsin
x)
=
arcsin(sin(-arcsin
x))
=
— arcsin
x
Поскольку то умножив на -1
, имеем: или Аргумент синуса попадает в допустимый интервал области значений арксинуса. Поэтому формула верна.
Аналогично для остальных функций.arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
x
arctg(-
x)
=
arctg(-tg arctg
x)
=
arctg(tg(-arctg
x))
=
— arctg
x
arcctg(-
x)
=
arcctg(-ctg arcctg
x)
=
arcctg(ctg(π-arcctg
x))
=
π — arcctg
x
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
a r c sin , a r c cos , a r c t g и a r c c t g
Для точного значения a r c sin , a r c cos , a r c t g и a r c c t g числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.
Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения a r c sin , a r c cos , a r c t g и a r c c t g отрицательных и положительных чисел сводится к нахождению формул a r c sin , a r c cos , a r c t g и a r c c t g противоположных чисел вида a r c sin ( — α ) = — a r c sin α , a r c cos ( — α ) = π — a r c cos α , a r c t g ( — α ) = — a r c t g α , a r c c t g ( — α ) = π — a r c c t g α .
Рассмотрим решение нахождения значений a r c sin , a r c cos , a r c t g и a r c c t g с помощью таблицы Брадиса.
Если нам необходимо найти значение арксинуса 0 , 2857 , ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0 , 2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.
Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0 , 2863 используется та самая поправка в 0 , 0006 , так как ближайшим числом будет 0 , 2857 . Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Таким образом находятся значения a r c sin , a r c cos , a r c t g и a r c c t g .
Урок и презентация на темы: «Арксинус. Таблица арксинусов. Формула y=arcsin(x)»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Что будем изучать:
1. Что такое арксинус?
2. Обозначение арксинуса.
3. Немного истории.
4. Определение.
6. Примеры.
Что такое арксинус?
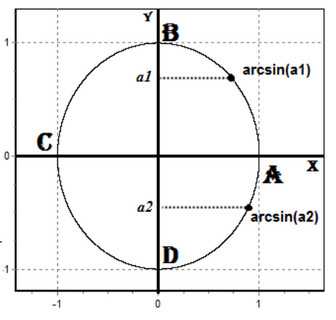
Ребята, мы с вами уже научились решать уравнения для косинуса, давайте теперь научимся решать подобные уравнения и для синуса. Рассмотрим sin(x)= √3/2. Для решения этого уравнения требуется построить прямую y= √3/2 и посмотреть: в каких точках она пересекает числовую окружность. Видно, что прямая пересекает окружность в двух точках F и G. Эти точки и будут решением нашего уравнения. Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk, а x2= 2π/3 + 2πk.
Решить данное уравнение довольно просто, но как решить, например, уравнение sin(x)= 5/6. Очевидно, что это уравнение будет иметь также два корня, но какие значения будут соответствовать решению на числовой окружности? Давайте внимательно посмотрим на наше уравнение sin(x)= 5/6. Решением нашего уравнения будут две точки: F= x1 + 2πk и G= x2 + 2πk, где x1 – длина дуги AF, x2 – длина дуги AG. Заметим: x2= π — x1, т.к. AF= AC — FC, но FC= AG, AF= AC — AG= π — x1.
Но, что это за точки?
Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается, как арксинус.
Тогда решение нашего уравнения запишется так: x1= arcsin(5/6), x2= π -arcsin(5/6).
И решение в общем виде: x= arcsin(5/6) + 2πk и x= π — arcsin(5/6) + 2πk.
Арксинус — это угол (длина дуги AF, AG) синус, которого равен 5/6.
Немного истории арксинуса
История происхождения нашего символа совершенно такая же, как и у arccos. Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга). Это вполне согласуется со смыслом понятия: arcsin x — это угол (а можно сказать и дуга), синус которого равен x.
Определение арксинуса
Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а.
Если |а|≤ 1, то уравнение sin(x)= a имеет решение: x= arcsin(a) + 2πk и x= π — arcsin(a) + 2πk
Перепишем:
x= π — arcsin(a) + 2πk = -arcsin(a) + π(1 + 2k).
Ребята, посмотрите внимательно на два наших решения. Как думаете: можно ли их записать общей формулой? Заметим, что если перед арксинусом стоит знак «плюс», то π умножается на четное число 2πk, а если знак «минус», то множитель — нечетный 2k+1. С учётом этого, запишем общую формула решения для уравнения sin(x)=a:
Есть три случая, в которых предпочитают записывать решения более простым способом:
sin(x)=0, то x= πk,
sin(x)=1, то x= π/2 + 2πk,
sin(x)=-1, то x= -π/2 + 2πk.
Для любого -1 ≤ а ≤ 1 выполняется равенство: arcsin(-a)=-arcsin(a).

Напишем таблицу значений косинуса наоборот и получим таблицу для арксинуса.
Примеры
1. Вычислить: arcsin(√3/2).
Решение: Пусть arcsin(√3/2)= x, тогда sin(x)= √3/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2.
Ответ: arcsin(√3/2)= π/3.
2. Вычислить: arcsin(-1/2).
Решение: Пусть arcsin(-1/2)= x, тогда sin(x)= -1/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= -π/6, т.к. sin(-π/6)= -1/2 и -π/2 ≤-π/6≤ π/2.
Ответ: arcsin(-1/2)=-π/6.
3. Вычислить: arcsin(0).
Решение: Пусть arcsin(0)= x, тогда sin(x)= 0. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.
4. Решить уравнение: sin(x) = -√2/2.x= arcsin(-√2/2) + 2πk и x= π — arcsin(-√2/2) + 2πk. Посмотрим в таблице значение: arcsin (-√2/2)= -π/4.
Ответ: x= -π/4 + 2πk и x= 5π/4 + 2πk.
5. Решить уравнение: sin(x) = 0.
Решение: Воспользуемся определением, тогда решение запишется в виде: x= arcsin(0) + 2πk и x= π — arcsin(0) + 2πk. Посмотрим в таблице значение: arcsin(0)= 0.
Ответ: x= 2πk и x= π + 2πk
6. Решить уравнение: sin(x) = 3/5.
Решение: Воспользуемся определением, тогда решение запишется в виде: x= arcsin(3/5) + 2πk и x= π — arcsin(3/5) + 2πk.
Ответ: x= (-1) n — arcsin(3/5) + πk.
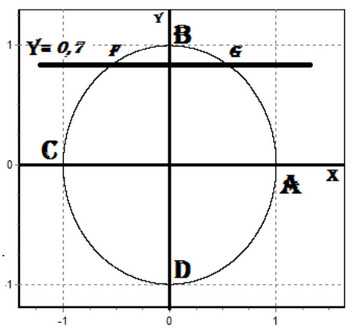
7. Решить неравенство sin(x)
Решение: Синус — это ордината точки числовой окружности. Значит: нам надо найти такие точки, ордината которых меньше 0.7. Нарисуем прямую y=0.7. Она пересекает числовую окружность в двух точках. Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа помогут разобраться в вычислении заданных функций. Значение тригонометрических функций угла равняется числу a , тогда автоматически считается величиной этого угла. Если a – число, тогда это и есть значение функции.
Для четкого понимания рассмотрим пример.
Если имеем арккосинус угла равного π 3 , то значение косинуса отсюда равно 1 2 по таблице косинусов. Данный угол расположен в промежутке от нуля до пи, значит, значение арккосинуса 1 2 получим π на 3 . Такое тригонометрическое выражение записывается как a r cos ( 1 2 ) = π 3 .
Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °
Арксинус
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

На этом уроке мы познакомимся с понятием арксинуса. Рассмотрим подробно функции у = sint на периоде и сформулируем прямую и обратную задачу для этой функции. Дадим определение для арксинуса как ответа для тригонометрического уравнения sint = a. Покажем нахождение арксинуса на числовой окружности
Докажем важное свойство арксинуса – равенство арксинуса от а и от минус а. Далее рассмотрим типовые задачи на вычисление арксинуса и другие задачи с использованием его свойств
А также докажем формулу, связывающую арксинус и арккосинус.
Уважаемые пользователи, на 13 минуте на доске в условии появляется описка. В примере б) вместо -0,8 следует писать -0,6. В ближайшее время видео будет исправлено.
Обратные функции отрицательного аргумента
Применяя указанные выше формулы и свойства тригонометрических функций, получаем формулы обратных функций отрицательного аргумента.
arcsin(-
x)
=
arcsin(-sin arcsin
x)
=
arcsin(sin(-arcsin
x))
=
— arcsin
x
Поскольку то умножив на -1
, имеем: или Аргумент синуса попадает в допустимый интервал области значений арксинуса. Поэтому формула верна.
Аналогично для остальных функций.arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
x
arctg(-
x)
=
arctg(-tg arctg
x)
=
arctg(tg(-arctg
x))
=
— arctg
x
arcctg(-
x)
=
arcctg(-ctg arcctg
x)
=
arcctg(ctg(π-arcctg
x))
=
π — arcctg
x
Решение уравнения cosx = a
Рассмотрим тригонометрическое уравнение, в левой части которого стоит ф-ция cosx, а в правой – число, например, 0,5:
По определению арккосинуса очевидно, что arccos 0,5 будет его решением, ведь
Так как arccos 0,5 = π/3, то мы находим очевидный корень х = π/3. И действительно, если подставить это значение в исходное ур-ние, то получится верное равенство:
Значит ли это, что мы решили ур-ние? Нет, ведь мы нашли только один корень, а их может быть несколько. Проведем на единичной окружности вертикальную прямую х = 0,5 и посмотрим, где она пересечет окружность:
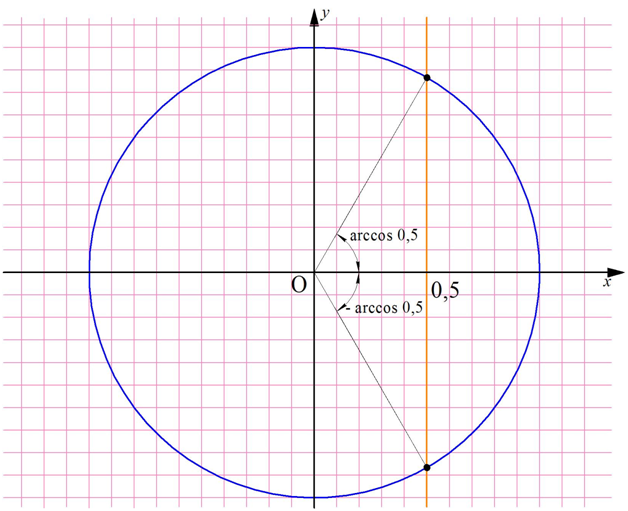
Видно, что есть ещё одна точка пересечения, соответствующая углу (– arccos 0,5). Это значит, что этот угол также является решением ур-ния. Проверим это:
Здесь мы использовали тот факт, косинус – четная функция, то есть
Итак, число – π/3 также является корнем ур-ния. Есть ли ещё какие-нибудь корни? Оказывается, есть. Построим график ф-ции у = cosx и посмотрим, где ее пересекает прямая у = 0,5:
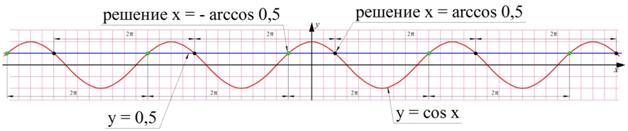
Оказывается, прямая пересекает график в бесконечном количестве точек! Это связано с периодичностью ф-ции у = cosx. Период этой ф-ции равен 2π, то есть
Поэтому, если число π/3 является решением ур-ния, то так же решением будут и число π/3 + 2π. Но к этому числу можно ещё раз добавить 2π и получить число π/3 + 4π. И оно тоже будет корнем. С другой стороны, период можно не только добавлять, но и вычитать, поэтому корнями ур-ния окажутся числа π/3 – 2π, π/3 – 4π и т.д. Как же записать все эти бесчисленные решения? Для этого используется такая запись:
Запись «π/3+ 2πn» называется серией решений. Она включает в себя бесконечное количество значений х, которые обращают ур-ние в справедливое равенство. Достаточно выбрать любое целое число и подставить его в серию решений. Например, при n = 0 получим решение
При n = 5 получим корень
При n = – 10 у нас получится решение
![]()
Однако помимо серии х = π/3 + 2πn решениями ур-ния будет определять ещё одна серия:
Действительно, число (– π/3) является корнем, но не входит в первую серию. Поэтому оно порождает собственную серию корней. Так, подставив в эту серию n = 4, получим корень
Итак, решением ур-ния являются две серии решений. Заметим, что каждой серии решений с периодом 2π соответствует ровно одна точка на единичной окружности:
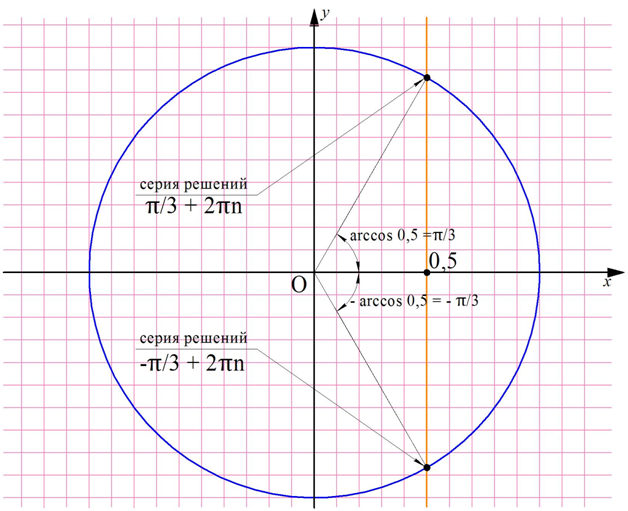
Объединить же обе серии можно одной записью:
Напомним, что мы решали ур-ние
и получили для него решение
Число π/3 появилось в записи по той причине, что arccos 0,5 = π/3. Поэтому в общем случае, когда ур-ние имеет вид
где а – некоторое число, его решением будут все такие х, что
![]()

Для краткости запись «n– целое число» заменяют эквивалентной записью
«n ∈ Z»
Напомним, что буквой Z обозначают множество целых чисел.
Задание. Решите ур-ние
Решение. Вспомним, что
Задание. Решите ур-ние
Решение. В таблице стандартных углов нет такого числа, у которого косинус равен 0,25. Поэтому вычислить значение arccos 0,25 мы не сможем. Но для записи решения и не нужно его вычислять:
Иногда встречаются задачи, в которых надо не просто решить ур-ние, но и выбрать некоторые его корни, удовлетворяющие определенному условию. Процедуру выбора корней, удовлетворяющих условию задачи, часто называют отбором корней. Заметим, что иногда при отборе корней удобнее записывать решение ур-ние не в виде одной серии, а в виде двух серий, у каждой из которых период равен 2π. Рассмотрим отбор корней на примере.
Задание. Укажите три наименьших положительных корня ур-ния
Решение. Так как
то все решения образуют две серии:
Начнем подставлять вместо n целые числа и выпишем из каждой серии несколько чисел. Так мы сможем найти наименьшие положительные числа в каждой серии.
Для первой серии:
Для второй серии:
Отметим все найденные корни на координатной прямой (схематично, не выдерживая масштаб):
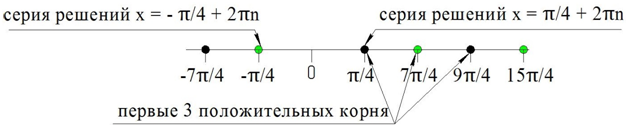
Видно, что тремя наименьшими положительными корнями являются числа π/4, 7π/4 и 9π/4
Ответ: π/4, 7π/4 и 9π/4.
Отметим, что возможны три частных случая, когда две серии решений сливаются в одну. Для ур-ния
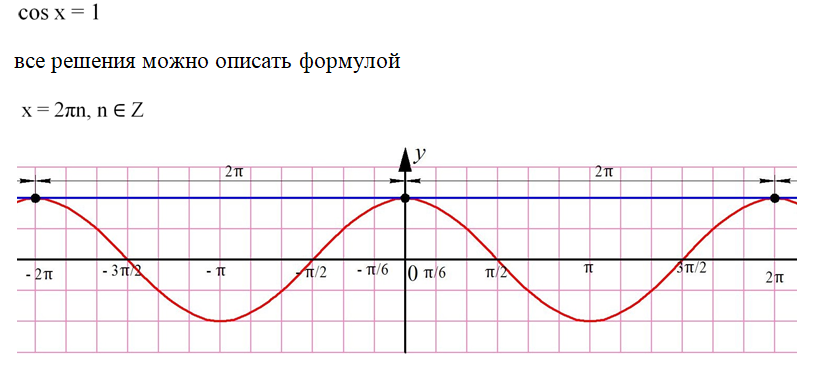
На графике видно, что этим значениям х соответствуют вершины синусоиды. Решениями же ур-ния
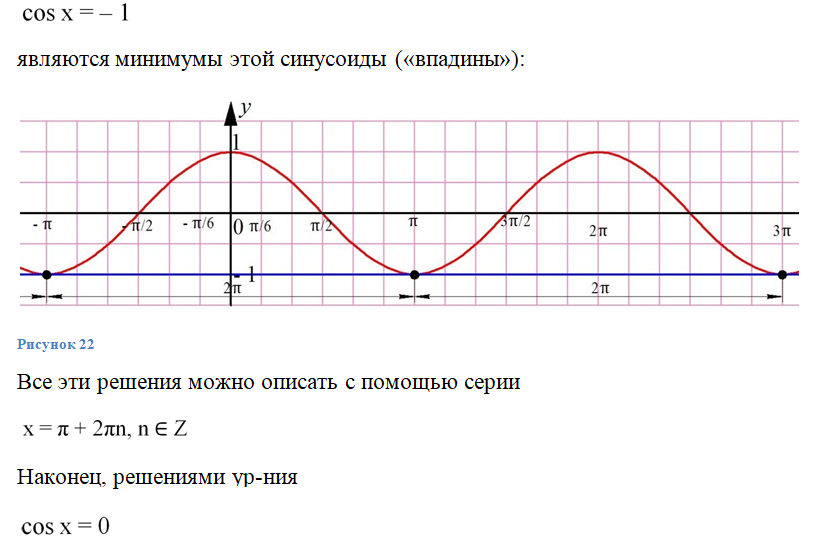
являются точки, в которых график пересекает ось Ох:
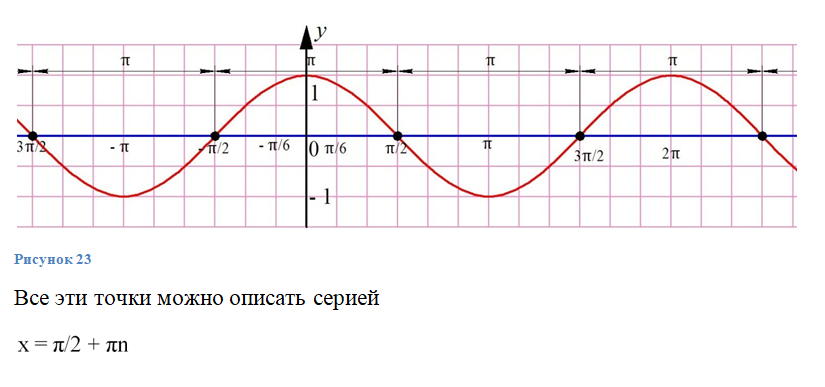
Отдельно отметим, что если правая часть в ур-нии – это число, большее единицы или меньшее (– 1), то ур-ние корней не имеет, ведь область определения косинуса – это отрезок .
Свойства арксинуса
Основные свойства арксинуса с формулами представлены в табличной форме ниже.
| Свойство | Формула |
| арксинус» data-order=»Синус арксинус»>Синус арксинус |
sin (arcsin x) = x» data-order=»sin (arcsin x) = x»>sin (arcsin x) = x |
| синус» порядок данных = «арксинус синус»>арксинус пазуха |
arcsin (sin x) = x + 2kπ, где k∈ℤ (k — целое число)» data-order=»arcsin (sin x) = x + 2kπ, где k∈ℤ (k — целое число)»> arcsin (sin x) = x + 2kπ, где k∈ℤ (k целое число) |
| отрицательное число» data-order=»Арксинус отрицательное число»> Арксинус отрицательное число |
arcsin (-x) = -arcsin x»data-order=»arcsin (-x) = -arcsin x»>arcsin(-x) = -arcsinx |
| Дополнительные углы | arcsin x = π/2 — arccos x = 90° — arccos x» data-order=»arcsin x = π/2 — arccos x = 90° — arccos x»> arcsin x = π/2 — arccos x = 90° — arccos x |
| арксинусы» data-order=»Сумма арксинусы»>Сумма арксинусы |
|
| arcsines» data-order=»Разница арксинус»>разность арксинусы |
|
| арксинус» data-order=»Косинус арксинус»>Косинус арксинус |
|
| арксинус» data-order=»тангенс арксинус»> Тангенс арксинус |
|
| арксинус» data-order=»Производный арксинус»>Производная арксинус |
|
| интеграл арксинуса» data-order=»Не определено интеграл арксинуса»>Не определено интеграл арксинуса |

