Графики и основные свойства элементарных функций

Введение

Пропорциональные величины

Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:

y = kx, 

где k — постоянная величина (коэффициент пропорциональности).

График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая

с осью X угол , тангенс которого равен k:

tg = k (рис.8).

Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = -3.

Линейная функция 

Если переменные y и x связаны уравнением 1-ой степени:

где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае — нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.

Обратная пропорциональность

Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением: y = k / x, где  k — постоянная величина. График обратной пропорциональности – гипербола (рис.10). 

У этой кривой две ветви. Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy= k.

Основные характеристики и свойства гиперболы:

1. область определения функции: , область значений: ;
2. функция монотонная (убывающая) при x < 0 и при x > 0, но не монотонная в целом из-за точки разрыва x = 0 (подумайте, почему?);
3. функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая;
4. нулей функция не имеет.

Квадратичная функция

Это функция:  

где a, b, c — постоянные, .

В простейшем случае имеем:  

График этой функции квадратная парабола — кривая, проходящая через начало координат (рис.11). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.

График функции  

— тоже квадратная парабола того же вида, что и , но её вершина лежит не в начале координат, а в точке с координатами:

Форма и расположение квадратной параболы в системе координат полностью зависит от двух параметров: коэффициента a при x2 и дискриминанта D. 

D = b2 – 4ac. 

Эти свойства следуют из анализа корней квадратного уравнения.

Основные характеристики и свойства квадратной параболы:

  — область определения функции: ( т.e. ), а область значений: … 

     (ответьте, пожалуйста, на этот вопрос сами!);

  — функция в целом не монотонна, но справа или слева от вершины ведёт себя, как монотонная;

  — функция неограниченная, всюду непрерывная, чётная при b = c = 0, и непериодическая;

  — при D < 0 не имеет нулей. (А что при ?).

Решение показательных неравенств

Показательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней.

Для решения показательных неравенств требуется знание следующей теоремы:

Теорема 2. Если a > 1, то неравенство af(x) > ag(x) равносильно неравенству того же смысла: f(x) > g(x). Если 0 < a < 1, то показательное неравенство af(x) > ag(x) равносильно неравенству противоположного смысла: f(x) < g(x).

Пример 7. Решите неравенство:

Решение: представим исходное неравенство в виде:

Разделим обе части этого неравенства на 32x, при этом (в силу положительности функции y = 32x) знак неравенства не изменится:

Воспользуемся подстановкой:

Тогда неравенство примет вид:

Итак, решением неравенства является промежуток:

переходя к обратной подстановке, получаем:

Левое неравенства в силу положительности показательной функции выполняется автоматически. Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству:

Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству:

Итак, окончательно получаем ответ:

Пример 8. Решите неравенство:

Решение: используя свойства умножения и деления степеней, перепишем неравенство в виде:

Введем новую переменную:

С учетом этой подстановки неравенство принимает вид:

Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство:

Итак, неравенству удовлетворяют следующие значения переменной t:

Тогда, переходя к обратной подстановке, получаем:

Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству:

Окончательно получаем ответ:

Пример 9. Решите неравенство:

Решение:

Делим обе части неравенства на выражение:

Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем:

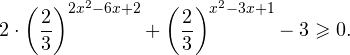
Воспользуемся заменой переменной:

Исходное уравнение тогда принимает вид:

Итак, неравенству удовлетворяют значения t, находящиеся в промежутке:

Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая:

Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе:

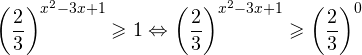
Поскольку основание степени в данном случае оказалось меньше единицы, но больше нуля, равносильным (по теореме 2) будет переход к следующему неравенству:

Итак, окончательный ответ:

Пример 10. Решите неравенство:

Решение:

Ветви параболы y = 2x+2-x2 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине:

Ветви параболы y = x2-2x+2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине:

Вместе с этим ограниченной снизу оказывается и функция y = 3×2-2x+2, стоящая в правой части уравнения. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 31 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1.

Ответ: x = 1.

Для того, чтобы научиться решать показательные уравнения и неравенства, необходимо постоянно тренироваться в их решении. В этом нелегком деле вам могут помочь различные методические пособия, задачники по элементарной математике, сборники конкурсных задач, занятия по математике в школе, а также индивидуальные занятия с профессиональным репетитором. Искренне желаю вам успехов в подготовке и блестящих результатов на экзамене.

Репетитор по математике в ТропарёвоСергей Валерьевич

Что такое экспонента: определение, формула, свойства, график

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Экспонента: определение, формула, свойства, график

В данной публикации мы рассмотрим, что такое экспонента, как выглядит ее график, приведем формулу, с помощью которой задается экспоненциальная функция, а также перечислим ее основные свойства.

• Определение и формула экспоненты
• График экспоненты
• Свойства экспоненциальной функции

Определение и формула экспоненты

Экспонента – это показательная функция, формула которой выглядит следующим образом:

f (x) = exp(x) = e x

где e – число Эйлера.

Экспоненциальная функция (так часто называют экспоненту) может быть определена:

Через предел (lim):

Через степенной ряд Тейлора:

График экспоненты

Ниже представлен график экспоненциальной функции y = e x.

Как мы видим график (синяя линия) является выпуклым, строго возрастающим, т.е. при увеличении x увеличивается значение y.

Асимптотой является ось абсцисс, т.е. график во II четверти координатной плоскости стремится к оси Ox, но никогда не пересечет и не коснется ее.

Пересечение с осью ординат Oy – в точке (0, 1), так как e = 1.

Касательная (зеленая линия) к экспоненте проходит под углом 45 градусов в точке касания.

Свойства экспоненциальной функции

1. Экспонента определена для всех x, причем функция везде возрастает, и ее значение всегда больше нуля. То есть:
   • область определения: – ∞ < x + ∞;
   • область значений: 0 < y < + ∞.
2. Обратная к экспоненте функция – это натуральный логарифм (ln x).
   • ln e x = x;
   • e ln x = x, где x > 0.
3. Для экспоненты применимы правила операций с показателями, например: e (a + b) = e a ⋅ e b.
4. Производная экспоненты:
   • (e x)‘ = e x.
   • если вместо x – сложная функция u: (e u)‘ = e u + u‘.
5. Интеграл экспоненты: ∫ e x dx = e x + C, где C – константа интегрирования.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Архив записей

Архив записейВыберите месяц Ноябрь 2022  (1) Сентябрь 2022  (1) Январь 2022  (2) Сентябрь 2021  (1) Июль 2021  (1) Июнь 2021  (2) Май 2021  (1) Апрель 2021  (1) Март 2021  (1) Сентябрь 2020  (1) Август 2020  (2) Июль 2020  (2) Июнь 2020  (2) Декабрь 2019  (3) Ноябрь 2019  (4) Октябрь 2019  (3) Сентябрь 2019  (2) Май 2019  (1) Октябрь 2018  (1) Июнь 2018  (1) Апрель 2018  (1) Январь 2018  (1) Ноябрь 2017  (1) Октябрь 2017  (1) Сентябрь 2017  (2) Август 2017  (4) Июль 2017  (5) Июнь 2017  (4) Май 2017  (5) Апрель 2017  (2) Март 2017  (1) Февраль 2017  (1) Январь 2017  (3) Декабрь 2016  (1) Ноябрь 2016  (2) Октябрь 2016  (3) Сентябрь 2016  (4) Август 2016  (6) Июль 2016  (9) Июнь 2016  (4) Май 2016  (5) Апрель 2016  (6) Март 2016  (5) Февраль 2016  (8) Январь 2016  (8) Декабрь 2015  (9) Ноябрь 2015  (4) Июль 2015  (1) Март 2015  (1) Февраль 2015  (1) Январь 2015  (1) Июль 2014  (1) Июль 2013  (1) Март 2013  (2) Декабрь 2012  (1) Ноябрь 2012  (1) Сентябрь 2012  (3) Август 2012  (4) Июль 2012  (4) Июнь 2012  (4) Май 2012  (4) Апрель 2012  (5) Март 2012  (7) Февраль 2012  (8) Январь 2012  (7) Декабрь 2011  (5) Ноябрь 2011  (1)

Решение элементарных уравнений неравенств

При решении простых показательных уравнений и неравенств используется графический метод.

Основной алгоритм в этом случае сводится к нахождению пересечений графиков функций.

В случае уравнений точки пересечения будут корнями уравнения.

В случае различий сначала строятся графики. Закрашивает области, ограниченные графами, и удовлетворяет условию неравенства. Определить, удовлетворяют ли сами графы существующим условиям. Заштрихованные области будут решением неравенства. Решение записывается в виде интервала или неравенства. При записи ответа необходимо учитывать, входят ли в найденный интервал пределы.

1

Мы видим, что график с основанием e больше похож на график с основанием 3, чем на график с основанием 2. Теперь, когда мы увидели родительский график и то, как он выглядит по сравнению с другими экспоненциальными функциями, давайте рассмотрим свойства экспоненциального графика. с основанием е. Сначала посмотрим, как меняется график в зависимости от значения константы «с» в уравнении. Из наших знаний по алгебре мы могли бы предсказать, что график будет сдвигаться вверх на единицу при каждом увеличении c. «Сдвинут вверх» относится более непосредственно к точке пересечения по оси y, поэтому форма графика, сохраняемая точкой пересечения с осью y, будет увеличиваться по мере увеличения c.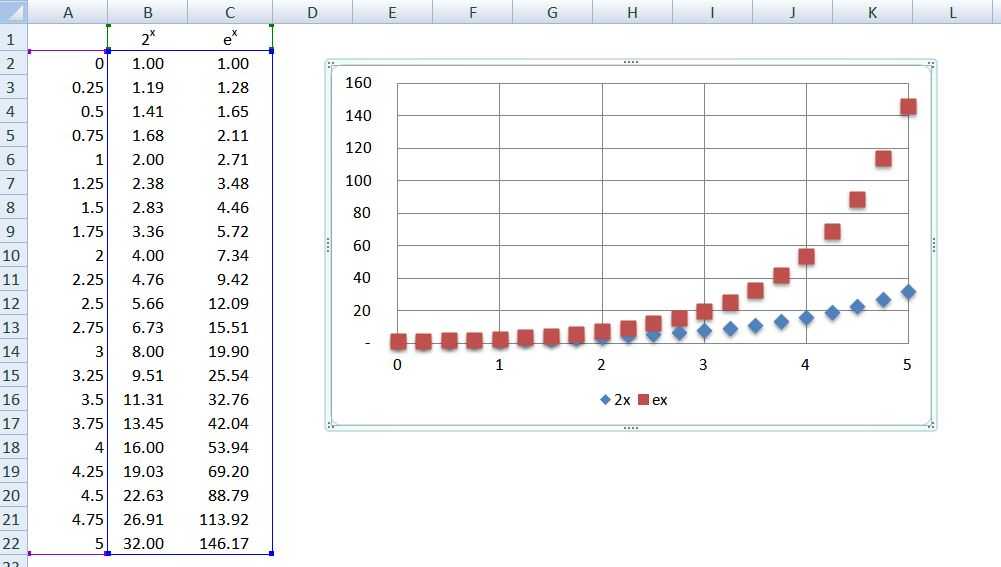

Теперь, вернувшись к нашему уравнению, мы видим, что точка пересечения с осью y, когда коэффициент при e равен 1, всегда будет равна c+1. Y-пересечение происходит из уравнения, когда x = 0. Мы имеем дело с экспоненциальным уравнением, где все в степени 0 равно 1. Так почему же тогда коэффициент при e должен быть равен 1? Давайте посмотрим на график, когда a=2 и c=1.

Отрезок по оси y увеличился на 1 по сравнению с нашим предыдущим уравнением, где a=1.

Мы можем видеть, что обратное действительно имеет место, когда c

Степенная, показательная и логарифмическая функции

Степенная функция

Это функция:  

где a, n – постоянные.

При n = 1 получаем прямую пропорциональность: y = ax;

при n = 2 — квадратную параболу;

при n = -1 — обратную пропорциональность или гиперболу. 

Таким образом, эти функции — частные случаи степенной функции. Мы знаем, что нулевая степень любого числа, отличного от нуля, равна 1, следовательно, при n = 0 степенная функция превращается в постоянную величину:  

y = a, т.e. её график — прямая линия, параллельная оси Х, исключая начало координат. Все эти случаи (при a = 1) показаны на рис.13 () и рис.14 ().

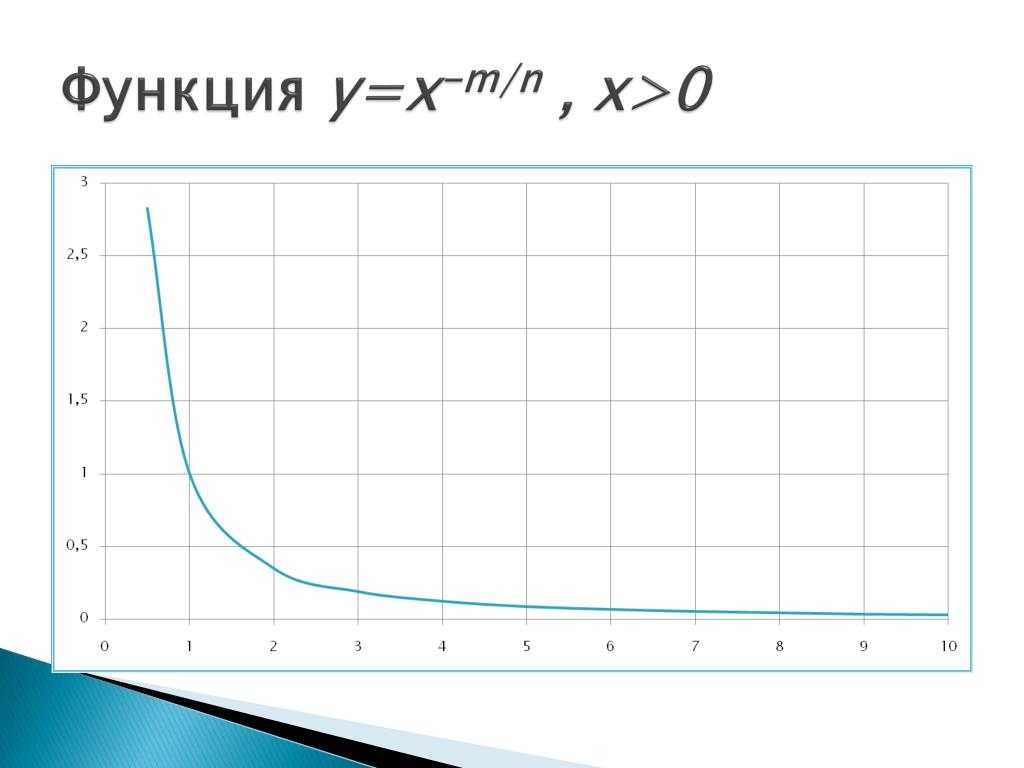
Отрицательные значения x здесь не рассматриваются, так как тогда некоторые функции:

Если n – целые, степенные функции имеют смысл и при x < 0, но их графики имеют различный вид в зависимости от того, является ли n чётным числом или нечётным.

На рис.15 показаны две такие степенные функции: для n = 2 и n = 3.

При n = 2 функция чётная и её график симметричен относительно оси Y. 

При n = 3 функция нечётная и её график симметричен относительно начала координат.

Функция y = x3 называется кубической параболой.

На рис.16 представлена функция

Эта функция является обратной к квадратной параболе y = x2, её график получается поворотом графика квадратной параболы вокруг биссектрисы 1-го координатного угла. Это способ получения графика любой обратной функции из графика её исходной функции.

Мы видим по графику, что это двузначная функция (об этом говорит и знак перед квадратным корнем).

Такие функции не изучаются в элементарной математике, поэтому в качестве функции мы рассматриваем обычно одну из её ветвей: верхнюю или нижнюю.

Показательная функция

Функция y = ax, где a — положительное постоянное число, называется показательной функцией.

Аргумент x принимает любые действительные значения; 

в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию.

Так, функция y = 81x имеет при x = 1/4 четыре различных значения: 

y = 3, y = -3, y = 3 i и y = -3 i (проверьте, пожалуйста!). Но мы рассматриваем в качестве значения функции только y = 3.

Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку (0, 1). При a = 1 мы имеем график прямой линии, параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 < a < 1 – убывает.

Основные характеристики и свойства показательной функции:

   — область определения функции: ( т.e. );

   — область значений: y > 0;

   — функция монотонна: возрастает при a > 1 и убывает при 0 < a < 1;

   — функция неограниченная, всюду непрерывная, непериодическая;

   — нулей функция не имеет.

Логарифмическая функция

Пусть а — положительное число, не равное 1.

Определение. Функцию, заданную формулой

называют логарифмической функцией с основанием а.

Перечислим основные свойства логарифмической функции:

1. Область определения логарифмической функции — множество всех положительных чисел R₊, т. е. D(log_a)=R₊. Действительно, каждое положительное число х имеет логарифм по основанию а.
2. Область значений логарифмической функции — множество всех действительных чисел. В самом деле, по определению логарифма любого действительного у справедливо равенство:

т. е. функция y = log_ax принимает значение у в точке x= aу0

3. Логарифмическая функция на всей области определения возрастает (при а>1) или убывает (при 0<а<1).

Докажем, например, что при а>1 функция возрастает (в случае 0 < а < 1 проводится аналогичное рассуждение).

Доказательство:

Пусть x₁ и x₂ — произвольные положительные числа и x₂>x₁. Надо доказать, что log_a x₂>log_a x₁. Допустим противное, т. е. что log_a x₂≤log_a x₁ (3)

Так как показательная функция у = ах при а>1 возрастает, из неравенства (3) следует: alog_a x₂ ≤ alog_a x₁. (4)

Но alog_a x₂ = x₂, alog_a x₁ = x₁ (по определению логарифма), т. е. неравенство (4) означает, что x₂ ≤ x₁. Это противоречит допущению x₂ > x₁.

Для построения графика заметим, что значение 0 логарифмическая функция принимает в точке 1;

log_a 1 = 0 при любом а > 0, так как а = 1.

Вследствие возрастания функции при а > 1 получаем, что при х > 1 логарифмическая функция принимает положительные значения, а при 0 отрицательные.

Если 0 < а <1, то y = log_ax убывает на R₊, поэтому log_a x > 0, при x > 1.

Опираясь на доказанные свойства, нетрудно построить график функции y = log_a х при а>1 (рис. 1, а) и 0<а<1 (рис. 1,6).

Справедливо следующее утверждение:

Графики показательной и логарифмической функций, имеющих одинаковое основание, симметричны относительно прямой у = х (рис. 2).