Разложение вектора по двум данным векторам

Понятие вектора. Свободный вектор

Сначала повторим школьное определение вектора. Вектором называется направленный отрезок, для которого указано его начало и конец:
В данном случае началом отрезка является точка , концом отрезка – точка . Сам вектор обозначен через . Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор , и это уже совершенно другой вектор. Понятие вектора удобно отождествлять с движением физического тела: согласитесь, зайти в двери института или выйти из дверей института – это совершенно разные вещи.

Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором . У такого вектора конец и начало совпадают.

!!! Примечание: Здесь и далее можете считать, что векторы лежат в одной плоскости или можете считать, что они расположены в пространстве – суть излагаемого материала справедлива и для плоскости и для пространства.

Обозначения: Многие сразу обратили внимание на палочку без стрелочки в обозначении  и сказали, там же вверху еще стрелку ставят! Верно, можно записать со стрелкой: , но допустима и запись , которую я буду использовать в дальнейшем. Почему? Видимо, такая привычка сложилась из практических соображений, слишком разнокалиберными и мохнатыми получались мои стрелки в школе и ВУЗе

В учебной литературе иногда вообще не заморачиваются клинописью, а выделяют буквы жирным шрифтом: , подразумевая тем самым, что это вектор.

То была стилистика, а сейчас о способах записи векторов:

1) Векторы можно записать двумя большими латинскими буквами: и так далее. При этом первая буква обязательно обозначает точку-начало вектора, а вторая буква – точку-конец вектора.

2) Векторы также записывают маленькими латинскими буквами: В частности, наш вектор  можно для краткости переобозначить маленькой латинской буквой .

Длиной или модулем ненулевого вектора  называется длина отрезка . Длина нулевого вектора  равна нулю. Логично.

Длина вектора обозначается знаком модуля: ,

Как находить длину вектора мы узнаем (или повторим, для кого как) чуть позже.

То были элементарные сведения о векторе, знакомые всем школьникам. В аналитической же геометрии рассматривается так называемый свободный вектор.

Если совсем просто – вектор можно отложить от любой точки:

Такие векторы мы привыкли называть равными (определение равных векторов будет дано ниже), но чисто с математической точки зрения это ОДИН И ТОТ ЖЕ ВЕКТОР или свободный вектор. Почему свободный? Потому что в ходе решения задач вы можете «пристроить» тот или иной «школьный» вектор в ЛЮБУЮ, нужную вам точку плоскости или пространства. Это очень крутое свойство! Представьте направленный отрезок произвольной длины и направления – его можно «клонировать» бесконечное количество раз и в любой точке пространства, по сути, он существует ВЕЗДЕ. Есть такая студенческая присказка: Каждому лектору в ж**у по вектору. Ведь не просто остроумная рифма, всё почти корректно – направленный отрезок можно пристроить и туда. Но не спешите радоваться, чаще страдают сами студенты =)

Итак, свободный вектор – это множество одинаковых направленных отрезков. Школьное определение вектора, данное в начале параграфа: «Вектором называется направленный отрезок…», подразумевает конкретный направленный отрезок, взятый из данного множества, который привязан к определённой точке плоскости или пространства.

Следует отметить, что с точки зрения физики понятие свободного вектора в общем случае некорректно, и точка приложения имеет значение. Действительно, прямой удар одинаковой силы по носу или по лбу хватит развивать мой дурацкий пример влёчет разные последствия. Впрочем, несвободные векторы встречаются и в курсе вышмата (не ходите туда :)).

Далее, если не оговаривается иное, речь пойдёт только о свободных векторах.

Ориентации базисов в пространстве

Базис в пространстве называется правым (или, что то же самое, упорядоченная тройка некомпланарных векторов называется правой тройкой), если, наблюдая из конца третьего вектора, кратчайший поворот от первого вектора ко второму виден происходящим против часовой стрелки (рис.1.33,а). Если описанный поворот виден происходящим по часовой стрелке, то базис называется левым (упорядоченная тройка некомпланарных векторов называется левой тройкой) (рис. 1.33,б).

Отметим следующие свойства: если тройка некомпланарных векторов — правая, то тройки, получающиеся «циклической» перестановкой трех векторов — также правые, а тройки, получающиеся перестановкой двух векторов или заменой одного вектора противоположным (например, — левые).

Источник

Анал_Геом / Изменение координат вектора при изменении базиса

Пусть в -мерном линейном пространстве выбран базис , который мы будем для удобства называть «старый» и другой базис , который мы будем называть «новый». Возьмем призвольный вектор из . Его координатный столбец в старом базисе обозначим , а в новом — . Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно «связать» друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису

Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса

Эта матрица называется матрицей перехода от старого базиса к новому.

Замечание 18.1 Матрица перехода всегда невырождена, то есть .

Предложение 18.5 Координатные столбцы в старом базисе и в новом базисе связаны формулой

где справа стоит произведение матрицы перехода на матрицу-столбец.

Доказательство. Так как — координатный столбец вектора в новом базисе, то

Заменив векторы их разложениями по старому базису, получим

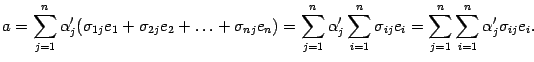
В силу предложения 14.3 изменим порядок суммирования

Здесь мы получили разложение вектора по старому базису, причем координата вектора с номером равна . Элемент с номером столбца будет иметь такой же вид. Следовательно, формула (18.1) доказана.

Пример 18.4 Пусть , то есть — трехмерное векторное пространство. Пусть задан ортонормированный базис i, j, k. Выберем другой (новый) базис

Возьмем вектор . Найдем его координаты в новом базисе.

Выпишем матрицу перехода, ее столбцы — это координаты новых базисных векторов

Пусть — координатный столбец вектора в новом базисе. Тогда

Найдем матрицу по формуле (14.14). Находим определитель

Находим алгебраические дополнения

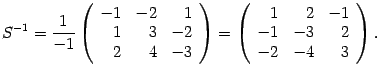
Находим координаты вектора

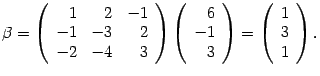
Таким образом, новые координаты вектора : , , , .

Тот же самый результат можно было получить, записав формулу (18.2) в виде системы уравнений

Решив эту систему, например, методом Гаусса, найдем новые координаты , , .

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Операции над векторами

Правила сложения векторов в стереометрии не отличаются от правил в планиметрии. Пусть надо сложить два вектора, а и b. Для этого отложим вектор а от какой-нибудь точки А, тогда его конец окажется в некоторой точке В. Далее от В отложим вектор b, его конец попадет в какую-то точку С. Тогда вектор АС как раз и будет суммой a и b:

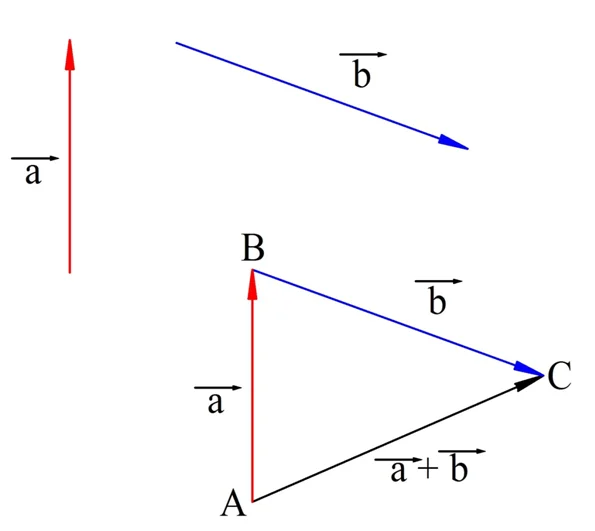
Такой метод сложения векторов именуется правилом треугольника. Если нужно сложить больше двух векторов, то используют правило многоугольника. В этом случае необходимо каждый следующий вектор откладывать от конца предыдущего. При этом в стереометрии вектора могут располагаться в различных плоскостях, то есть они на самом деле многоугольник не образуют:

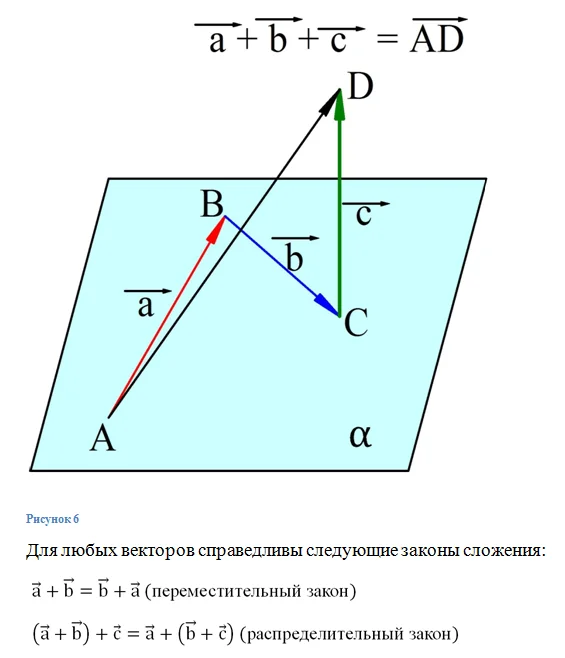
Напомним, что в планиметрии существовали так называемые противоположные вектора. Есть они и в стереометрии:

Главное свойство противоположных векторов заключается в том, что в сумме они дают нулевой вектор:

Заметим, что для получения противоположного вектора достаточно поменять его начало и конец, то есть в записи вектора обозначающие его буквы надо просто записать в обратном порядке:

C помощью противоположного вектора легко определить операцию вычитания векторов. Чтобы из вектора а вычесть вектор b, надо всего лишь прибавить к a вектор, противоположный b

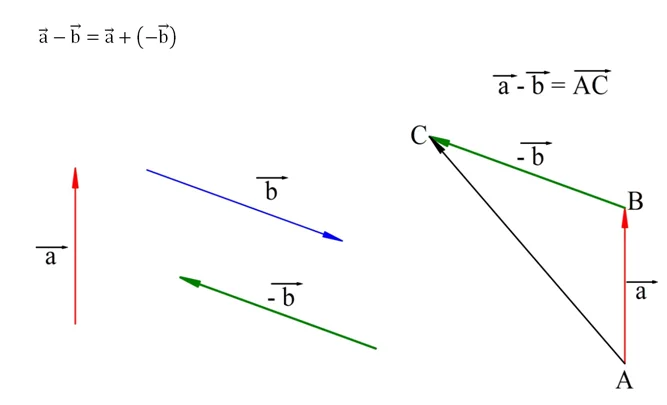
Далее рассмотрим умножение вектора на число. Пусть вектор а умножается на число k. В результате получается новый вектор b, причем

1) b и a будут коллинеарными векторами;

2) b будет в k раз длиннее, чем вектор a.

Если k – положительное число, то вектора a и b будут сонаправленными. Если же k< 0, то a и b будут направлены противоположно.

Уточним, что если |k| < 1, то фактически b будет не длиннее, а короче вектора a. Наконец, если k = 0, то и b будет иметь нулевую длину, то есть b окажется нулевым вектором.

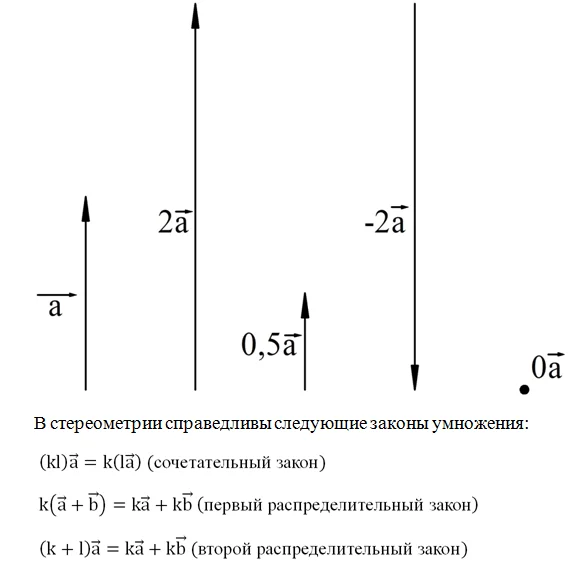
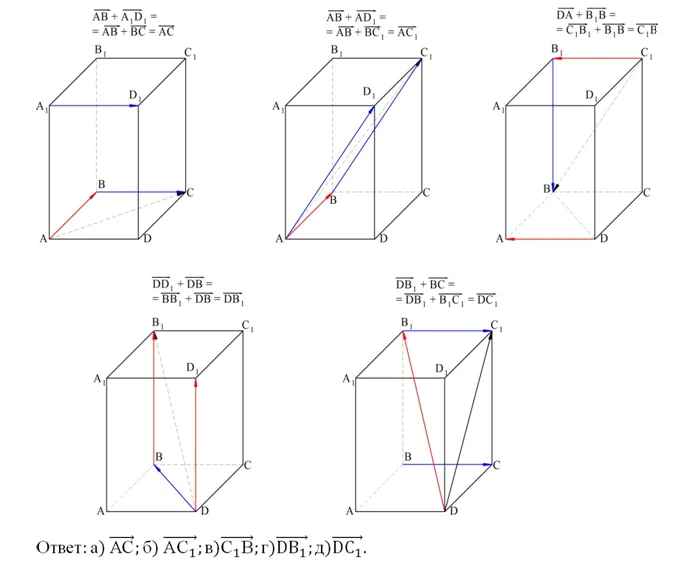
Задание. Дан параллелепипед АВСDА₁В₁С₁D₁. Постройте вектор, который будет являться суммой векторов:

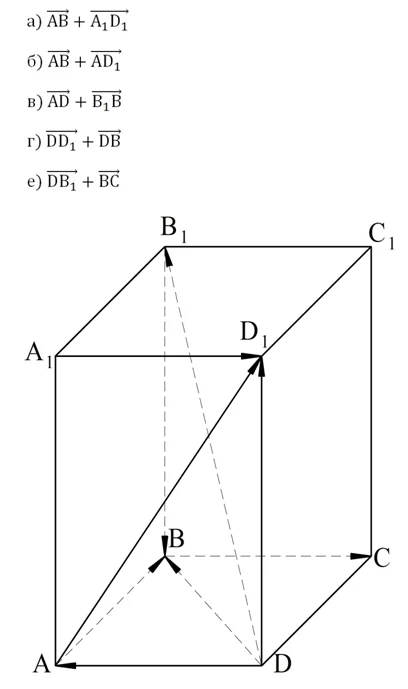
Решение. В каждом случае необходимо заменить один из векторов в сумме на другой равный ему вектор так, чтобы можно было применить правило треугольника.

В задании а) вектор А₁D₁ заменить равным ему вектором ВС. В итоге получится вектор АС.

В задании б) заменяем АD₁ на вектор ВС₁. Также можно было бы заменить АВ на D₁C₁. В обоих случаях сумма окажется равной АС₁.

В задании в) удобно DA заменить на C₁В₁, тогда искомой суммой будет вектор С₁В.

В задании г) производим замену DD₁ на равный ему вектор BB₁. Тогда сумма DB и BB₁– это вектор DB₁.

В задании д) необходимо заменить ВС на В₁С₁. В итоге получаем вектор DC:

Задание. В пространстве отмечены точки А, В, С и D. Выразите вектор АВ через вектора:

Решение. В случае а) сначала запишем очевидное равенство векторов, вытекающее из правило многоугольника:

Обратите внимание, что здесь у каждого следующего слагаемого начальная точка совпадает с конечной точкой предыдущего слагаемого, поэтому равенство и справедливо:

Однако по условию а) нам надо использовать другие вектора для выражения АВ. Мы можем просто заменить вектора CD и DB на противоположные:

Теперь можно составить и выражение для АВ:

Аналогично решаем и задания б) и в):

Задание. Р – вершина правильной шестиугольной пирамиды. Докажите, что сумма векторов, совпадающих с ребрами этой пирамиды и начинающихся в точке Р, в точности равна сумме векторов, которые совпадают с апофемами пирамиды и при этом также начинаются в точке Р.

Решение. Обозначим вершины буквами А₁, А₂, … А₆, а середины сторон шестиугольника, лежащего в основании, буквами Н₁, Н₂, … Н₆, как это показано на рисунке:

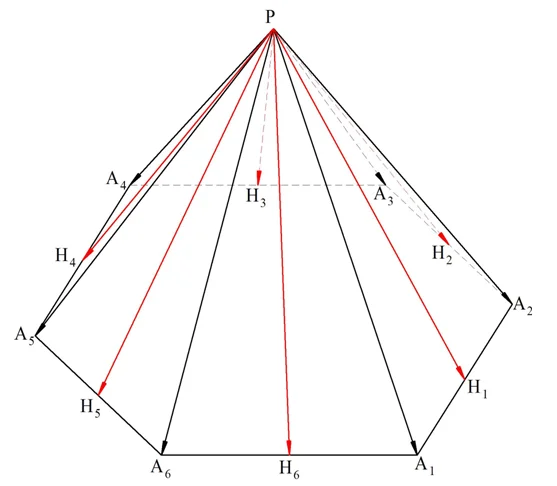
Нам надо показать, что сумма красных векторов равна сумме черных векторов:

Теперь отдельно построим правильный шестиугольник, лежащий, в основании пирамиды:

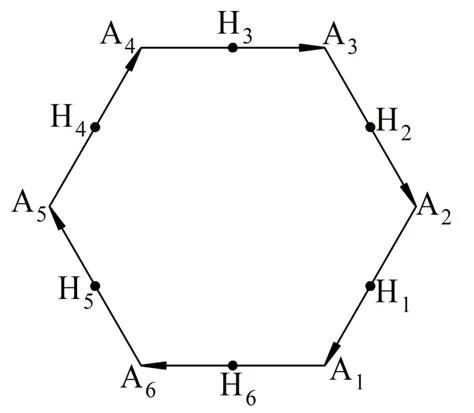
Ясно, что вектора, образованные сторонами этого шестиугольника, в сумме дают нулевой вектор (по правилу многоугольника):

Так как точки Н₁, Н₂, … Н₆ – середины сторона, то вектора Н₆А₆, Н₅А₅,…Н₁А₁ будут вдвое короче векторов А₁А₆, А₆А₅, … А₂А₁. При этом они находятся на одних прямых, поэтому справедливы равенства:

Таким образом нам удалось из верного равенства (3) доказать (2), из которого в свою очередь следует справедливость и (1), ч. т. д.

Задание. Упростите выражения:

Решение. Здесь надо просто применить законы сложения и умножения векторов, как это делалось и в курсе планиметрии. Сначала раскрываем скобки, а потом приводим подобные слагаемые:

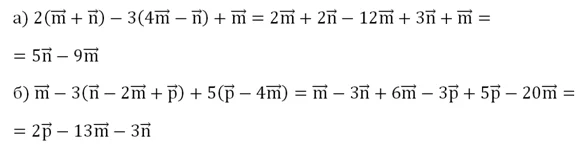
Разложение вектора на некомпланарные вектора

Иногда вектор можно разложить не на два, а на три вектора. Выглядит такое разложение так:

Для доказательства рассмотрим три некомпланарных вектора а, bи c, а также произвольный вектор р. Отложим их от одной точки О. Обозначим концы этих векторов большими буквами А, В, С и Р:

Через ОВ и ОА можно провести некоторую плос-ть α. Точка С ей принадлежать не может, ведь ОА, ОВ и ОС – некомпланарные вектора. Проведем через Р прямую, параллельную ОС. Так как ОС пересекает α, то и параллельная ей прямая также пересечет α в некоторой точке Р₁. (Примечание. Если Р принадлежит α, то точки Р и Р₁ совпадут, то есть вектор Р₁Р будет нулевым).

Далее через точку Р₁ в плос-ти α проведем прямую, параллельную ОВ, которая пересечет ОА в точке Р₂. Заметим, что вектор ОР₂ находится на той же прямой, что и вектор ОА, то есть они коллинеарны, поэтому существует такое число х, что

Итак, мы показали, что у произвольного вектора p есть разложение на заранее заданные некомпланарные вектора. Осталось показать, что существует только одно такое разложение. Докажем это методом от противного. Пусть есть второе разложение с другими коэффициентами х₁, у₁ и z₁:

В правой части находятся три вектора, которые в сумме нулевой вектор. По правилу сложения векторов это означает, что эти вектора образуют треугольник, то есть находятся в одной плос-ти:

Значит, они компланарны. Тогда компланарны и вектора a, b и с, что противоречит условию теоремы. Значит, второго разложения р на заданные некомпланарные векторы не существует, ч. т. д.

Задание. АВСD и А₁В₁С₁D₁ – параллелограммы, располагающиеся в разных плос-тях. Докажите, что тройка векторов ВВ₁, СС₁ и DD₁ компланарна.

Решение. Сначала построим рисунок по условию задачи:

Для доказательства используем признак компланарности векторов. Для этого надо один из векторов, отмеченных на рисунке красным, разложить на два других вектора.

В результате нам удалось разложить СС₁ на вектора BB₁ и CC₁. Значит, эти три вектора коллинеарны.

Задание. В параллелепипеде АВСDA₁B₁C₁D₁ запишите разложение вектора BD₁ по векторам ВА, ВС и ВВ₁.

Решение. Сначала представим вектор BD₁ как сумму трех векторов:

Теперь заметим, что вектора С₁D₁ и ВА соответствуют ребрам параллелепипеда. Эти ребра одинаковы по длине и параллельны, поэтому и вектора будут равными. Аналогично равны вектора СС₁ и ВВ₁:

Задание. АВСD – тетраэдр, а точка К делит его ребро ВС пополам. Разложите вектор DK по векторам DA, AB и AC.

Решение. Сначала запишем очевидное выражение для вектора DK:

Задание. В точке М пересекаются медианы треугольника АВС, а О – произвольная точка в пространстве. Разложите вектор ОМ по векторам ОА, ОВ и ОС.

Решение. Медиану, проходящую через точку А, мы обозначим как АА₁, то есть А₁ – это середина отрезка ВС. Также буквой К обозначим середину ОВ:

Сначала разложим вектор ОА₁ на ОВ и ОС. Это можно сделать, ведь они компланарны. КА₁ – это средняя линия ∆ОСВ, поэтому КА₁||ОС и КА₁ вдвое короче ОС. Это значит, что

Так как АА₁ – медиана, то точка М делит ее в отношении 2:1. Отсюда вытекает следующее соотношение:

Только что решенная задача может быть использована и при решении другого, более сложного задания.

Задание. Докажите, что в параллелепипеде АВСDА₁В₁С₁D₁ плос-ти А₁ВD и СB₁D₁ делят диагональ АС₁ на три равных отрезка.

Решение. Обозначим точкой K точку пересечения медиан ∆А₁ВD. Тогда по формуле, выведенной в предыдущей задаче, мы получаем, что

Это соотношение означает, что вектора АК и АС₁ коллинеарны, поэтому они располагаются на одной прямой (они не могут находиться на параллельных прямых, ведь у них есть общая точка А). Значит, точка K принадлежит диагонали АС₁, и отрезок АК втрое короче диагонали.

Аналогично можно показать, что и

Из этого также вытекает, что М принадлежит диагонали АС₁, и МС₁ втрое короче АС₁. Значит, точки М и К делят диагональ на три равных отрезка, ч. т. д.

Сегодня мы расширили понятие векторов и научились их применять не только в планиметрических, но и в стереометрических задачах. При сохраняются все правила, по которым выполняются действия над векторами. Также в стереометрии появляется новое понятие компланарных и некомпланарых векторов.

Как разложить вектор по двум базисным векторам: принцип, пример

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.

В данной публикации мы рассмотрим, каким образом можно разложить вектор по двум базисным векторам, а также разберем пример решения задачи по этой теме.

• Принцип разложения вектора
• Пример задачи

Принцип разложения вектора

Для того, чтобы разложить вектор b по базисным векторам a₁, …, a_n, требуется определить такие коэффициенты x₁, …, x_n, при которых линейная комбинация векторов a₁, …, a_n равняется вектору b, то есть:

x₁a₁ + … + x_na_n = b

где x₁, …, x_n – координаты вектора b в базисе a₁, …, a_n

Пример задачи

Разложим вектор b = {16; 1} по двум базисным векторам m = {2; 1} и n = {1; -3}.

Решение:

1.

xm + yn = b

2. Представим его в виде системы линейных уравнений:

3. Теперь нужно решить систему. Из второго уравнения получаем:x = 1 + 3y.

Подставляем полученное выражение в первое уравнение:2 · (1 + 3y) + y = 162 + 6y + y = 167y = 14y = 2

Следовательно, x = 1 + 3y = 1 + 2 · 2 = 7.

Ответ: b = 7m + 2n.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Сложение и вычитание векторов

Пусть у нас есть векторы a{x₁; у₁} и b{x₂; у₂}. Можно ли, зная только их координаты, определить их сумму и разность? Оказывается, можно. Действительно, по определению координат векторов (напомним, они являются коэффициентами разложения вектора на орты) можно записать:

Эта запись означает, что с имеет координаты {х₁ + х₂; у₁ + у₂}. В результате мы можем сформулировать правило сложения векторов:

Проиллюстрируем правило на примере. Пусть надо сложить вектора а {2; 3} и b {4; 5}. Понятно, что в результате получится новый вектор, который мы обозначим как с {х; у}. Чтобы найти его первую координату, надо сложить первые координаты векторов a и b:

x = 2 + 4 = 6

Для нахождения второй координаты складываем соответственно вторые координаты векторов:

y = 3 + 5 = 8

В итоге получился вектор с {6; 8}.

Задание. Сложите вектора, имеющие координаты:

Решение. Сначала просто складываем первые числа в скобках (и получаем координату х), а потом – вторые (и получаем координату у):

Теперь попытаемся понять, как вычислять разность двух векторов. Пусть есть вектора с заранее заданными координатами a{x₁; у₁} и b{x₂; у₂}. Снова запишем их разложение на единичные вектора:

Теперь мы можем сформулировать правило вычитания векторов:

Например, пусть надо вычесть из вектора а{5; 3} вектор b{2;1}. Искомая разность будет представлять собой вектор, чья координата х будет равна разности первых координат векторов а и b:

x = 5 — 2 = 3

Аналогично вычисляем и координату у:

y = 3 — 1 = 2

В итоге получили вектор с координатами {3; 2}.

Задание. Вычтите из вектора а вектор b, если известны их координаты:

Решение. Во всех случаях мы сначала из первой координаты вектора а вычитаем первую координату b, в результате чего получаем координату х искомого вектора. Далее повторяем процесс со второй координатой (то есть с у):

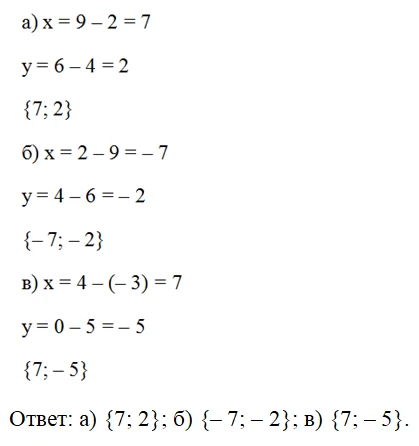
Далее рассмотрим такую операцию, как умножение вектора на число. Снова запишем, что вектор а с координатами х₁и у₁ можно разложить на орты следующим образом:

Это означает, что при умножении вектора на число надо просто умножить на это число каждую его координату.

Например, есть вектор а{3; 7}, который надо умножить на 5. Умножим на 5 по отдельности каждую координату:

x = 5*3 = 15

y = 5*7 = 35

В результате получился вектор {15; 35}.

Задание. Умножьте вектор а на число k, если известно, что:

Решение. Надо всего лишь умножить каждую координату а на число k, и таким образом получить новые координаты:

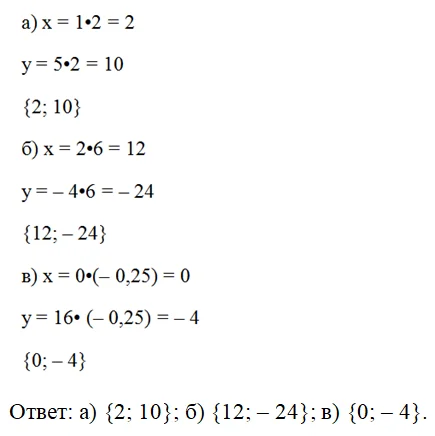
Примеры разложения вектора на два составляющих

Разложение вектора на два составляющих является важной задачей в линейной алгебре и находит применение во многих сферах, таких как механика, физика, геометрия и т.д. Ниже приведены примеры разложения вектора на два составляющих для различных задач

• Пример 1: Разложить вектор AB на составляющие по векторам AC и AD.

Вектор	x	y	z
AB	3	-4	2
AC	1	2	-1
AD	2	3

Используя формулы разложения вектора на составляющие, находим:

Proj_ACAB = (AB·AC/|AC|2) AC = (3*1 + (-4)*2 + 2*(-1))/6 (1,2,-1) = (-1/3, -2/3, 1/3)

Proj_ADAB = (AB·AD/|AD|2) AD = (3*2 + (-4)*0 + 2*3)/13 (2,0,3) = (12/13, 0, 18/13)

Таким образом, вектор AB может быть представлен как сумма двух векторов, направленных вдоль векторов AC и AD соответственно:

AB = Proj_ACAB + Proj_ADAB = (-1/3, -2/3, 1/3) + (12/13, 0, 18/13) ≈ (1.29, -0.67, 2.08)

Пример 2: Разложить вектор (2,5,-3) на составляющие по векторам (1,-1,1) и (-2,4,-1).

Применим теорему Пифагора, чтобы найти проекцию вектора на каждое из направляющих:

Proj_(1,-1,1)(2,5,-3) = ((2-5+3)(1,-1,1))/3 = (0,0,0)

Proj_(-2,4,-1)(2,5,-3) = ((-4+20+3)(-2,4,-1))/21 = (-10/21, 20/21, -5/21)

Тогда вектор (2,5,-3) может быть представлен как:

(2,5,-3) = Proj_(1,-1,1)(2,5,-3) + Proj_(-2,4,-1)(2,5,-3) = (-10/21, 20/21, -5/21)

Пример 3: Разложить вектор OA на составляющие по векторам OB и OC.

При разложении вектора OA на составляющие по векторам OB и OC можно использовать правило параллелограмма:

OA = OB + OC = OD + OC

где OD — проекция вектора OA на вектор OB. Это означает, что мы можем найти проекцию вектора OA на вектор OB и вычислить оставшуюся составляющую.

Проекция вектора OA на вектор OB:

Proj_OBOA = (OA·OB/|OB|2) OB = ((2*1 + (-1)*2 + 3*2)/9) (1,-2,2) = (2/3, -4/3, 4/3)

Тогда оставшаяся составляющая равна:

OA — Proj_OBOA = (5,3,-1) — (2/3, -4/3, 4/3) = (13/3, 13/3, -7/3)

Таким образом, вектор OA может быть представлен как сумма двух векторов, направленных вдоль векторов OB и OC соответственно:

OA = Proj_OBOA + (OA — Proj_OBOA) = (2/3, -4/3, 4/3) + (13/3, 13/3, -7/3) ≈ (5.33, 4.33, -1.33)

Понятие базиса системы векторов

Тема базиса системы векторов связана с понятием линейной независимости векторов и линейной комбинации.

Определение 1. Три линейно независимых вектора (система векторов) , и образуют в пространстве базис, если любой вектор
может быть представлен в виде некоторой линейной комбинации векторов , и ,
т.е. если для любого вектора найдутся такие вещественные числа
, и ,
что справедливо равенство

.   (2)

Аналогично определяется базис на некоторой плоскости.

Определение 2.. Два лежащих в плоскости линейно независимых вектора (система векторов) и образуют на этой плоскости базис, если любой лежащий в этой же плоскости вектор
может быть представлен в виде некоторой линейной комбинации векторов и ,
т.е. если для любого лежащего в этой плоскости вектора
найдутся такие вещественные числа и ,
что справедливо равенство

.   (3)

Справедливы следующие утверждения:

1) любая тройка некомпланарных векторов , и
образует базис в пространстве,

2) любая пара лежащих в данной плоскости неколлинеарных векторов и
образует базис на этой плоскости.

Определение 3. Векторное пространство называется n-мерным, если в нём существует в точности n линейно независимых векторов.

Базисом  n-мерного пространства называется любая система из n независимых векторов этого пространства.

Пример 1.  Доказать, что векторы

образуют базис в четырёхмерном пространстве.

Решение. Система векторов образует базис, если: 1) количество векторов равно размерности пространства; 2) эти векторы линейно независимы. Первое требование выполнено, остаётся доказать, что эти векторы линейно независимы. Попытаемся составить из них линейную нулевую комбинацию:

Подставим в это равенство вместо данных векторов их выражения в координатах и преобразуем левую часть:

или

 
Но вектор является нулевым, когда все его проекции равны нулю, т.е.

Таким образом, из данных векторов невозможно составить нулевую линейную комбинацию, у которой хотя бы один коэффициент был отличен от нуля. Поэтому векторы

линейно независимы и, следовательно, образуют базис в четырёхмерном пространстве.

Теорема (о вычислении проекции вектора через косинус)

Проекция ненулевого вектора на ось равна длине этого вектора, умноженной на косинус угла между этим вектором и осью.

Доказательство

Пусть дан вектор $\vec{v}=\overrightarrow{AB}\neq\vec{0}$, $\vec{e}$ – единичный вектор координатной оси $x$, и $\varphi=\angle(\vec{v}, \vec{e})$.

Докажем, что проекция $v_x$ вектора $\vec{v}$ на ось $x$ вычисляется по формуле $v_x=|\vec{v}|\cos{\varphi}$ $(1)$.

Возможны следующие случаи:

1) Угол $\varphi = 0^\circ$. Тогда $\overrightarrow{AB}=\vec{e}$, $\overrightarrow{A_1B_1}=\overrightarrow{AB}=\vec{v}$ и $v_x=|\vec{v}|$. Так как $\cos{0^\circ}$=1, то $v_x=|\vec{v}|\cos{\varphi}$.

2) Угол $\varphi$ острый. Пусть точка $A$ не лежит на оси $x$. Через точку $A$ проведем прямую $p$, параллельную оси $x$. Пусть точка $C$ – проекция точки $B$ на прямую $p$. Получим прямоугольный треугольник $ABC$ с углом $\varphi$ при вершине $A$ и прямоугольник $AA_1B_1C$. Тогда $v_x=|\overrightarrow{A_1B_1}|=AC=AB\cos{\varphi}=|\vec{v}|\cos{\varphi}$, то есть $v_x=|\vec{v}|\cos{\varphi}$.

Если точка $A$ лежит на оси $x$? то равенство $(1)$ вытекает из прямоугольного треугольника $ABB_1$.

3) Угол $\varphi=90^\circ$. В этом случае $\overrightarrow{AB}=\vec{e}$, $A_1=B_1$ и $v_x=0$. И так как $\cos{90^\circ}=0$, то равенство $(1)$ выполняется.

4) Угол $\varphi$ тупой. Сначала через точку $A$ проводим прямую $p$, параллельную оси $x$, и проецируем на нее точку $B$ в точку $C$юСнова получим прямоугольный треугольник $ABC$. Его угол при вершине $A$ равен $180^\circ-\varphi$. Поэтому $AC=AB\cos{(180^\circ-\varphi)}=-AB\cos{\varphi}$. В рассматриваемом случае $\overrightarrow{A_1B_1}\updownarrows\vec{e}$, и поэтому $v_x=-|\overrightarrow{A_1B_1}|=-AC=AB\cos{\varphi}=|\vec{v}\cos{\varphi}|$, то есть снова выполняется равенство $(1)$.

Если же точка $A$ лежит на прямой $x$ то доказательство только упрощается соответственным образом.

5) Угол $\varphi=180^\circ$. Тогда $\overrightarrow{AB}\updownarrows\vec{e}$, $\overrightarrow{A_1B_1}=\overrightarrow{AB}=\vec{v}$ и $v_x=-|\vec{v}|$. Так как $\cos{180^\circ}=-1$, то равенство $(1)$ снова имеет место.

Свойство 1

Равные векторы имеют равные проекции на заданную ось.

Доказательство

Проекция вектора $\vec{v}$ зависит лишь от длины этого вектора и угла $\varphi$, который он образует с данной осью, так как $v_x=|\vec{v}|\cos{\varphi}$. Равные же векторы имеют, во-первых, равные длины и, во-вторых, образуют с осью один и тот же угол (в силу параллельности прямых). Следовательно, их проекции равны.

Свойство 2

При сложении векторов их проекции на ось складываются.

Доказательство

Сложим любые два вектора $\vec{a}=\overrightarrow{AB}$ и $\vec{b}=\overrightarrow{BC}$. Получим вектор $\vec{c}=\vec{a}+\vec{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$. Пусть точки $A_1, B_1, C_1$ – проекции точек $A, B, C$ на ось $x$, а $x_A, x_B, x_C$ – их координатыб и $a_x, b_x, c_x$ – проекции векторов $\vec{a}, \vec{b}, \vec{c}$ на ось $x$.

Так как $a_x=x_B-x_A, b_x=x_C-x_B$, то $a_x+b_x=x_B-x_A+x_C-x_B=x_C-x_A$.

C другой стороны $c_x=x_C-x_A$.

Поэтому $c_x=a_x+b_x$.

Свойство 3

При умножении вектора на число его проекция умножается на это число.

Доказательство

Пусть $x$ – ось с начальной точкой $O$ и единичным вектором $\vec{e}$. Возьмем любой вектор $\vec{a}$ и отложим его от точки $O$: $\overrightarrow{OA}=\vec{a}$. Пусть $\varphi$ – угол между векторами $\vec{a}$ и $\vec{e}$. Умножим вектор $\vec{a}$ на число $\alpha$. Получим вектор $\vec{b}=\overrightarrow{OB}=\alpha\vec{a}$. Необходимо доказать, что $b_x=\alpha a_x$.

Возможны следующие случаи:

1) $\alpha>0$. Тогда $\angle(\vec{b},\vec{e})=\varphi$. Кроме того, $|\vec{b}|=|\alpha||\vec{a}|$, то есть $OB=\alpha OA$. Поэтому $b_x=|\vec{b}|\cos{\varphi}=OB\cos{\varphi}=\alpha OA\cos{\varphi}=\alpha a_x$.

2) $\alpha<0$. Тогда $\angle(\vec{b},\vec{e})=180^\circ-\varphi$. Кроме того, $|\vec{b}|=|\alpha||\vec{a}|$, то есть $OB=|\alpha| OA$. А так как $\alpha<0$, то $|\alpha|=-\alpha$ и поэтому $OB=-\alpha OA$. Следовательно, $b_x=|\vec{b}|\cos{(180^\circ-\varphi)}=-OB\cos{\varphi}=\alpha OA\cos{\varphi}=\alpha a_x$.

3) $\alpha=0$. Тогда $\vec{b}=\alpha \vec{a}=\vec{0}$, и поэтому $b_x=0$ и $b_x=\alpha a_x$.

Проекция линейной комбинации векторов, равна соответствующей линейной комбинации проекций этих векторов.

Разложение вектора по базису

Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Докажем эту теорему:

зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :

x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:

1 — x 1 ) · e ( 1 ) + ( x

2 — x 2 ) · e ( 2 ) + . . . ( x

Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x

2 — x 2 ) , . . . , ( x

n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x

n . И это доказывает единственный вариант разложения вектора по базису.

При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .

Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .

Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x

Вектор x → будет представлен следующим образом:

2 · e ( 2 ) + . . . + x

Запишем это выражение в координатной форме:

( x 1 , x 2 , . . . , x n ) = x

1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x

2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x

n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x

2 e 1 ( 2 ) + . . . + x

2 e 2 ( 2 ) + + . . . + x

n e 2 ( n ) , . . . , x

2 e n ( 2 ) + . . . + x

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x

n e 2 n ⋮ x n = x

Матрица этой системы будет иметь следующий вид:

e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )

Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x

n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .

Применим рассмотренную теорию на конкретном примере.

Исходные данные: в базисе трехмерного пространства заданы векторы

e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )

Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.

Решение

Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .

Используем метод Гаусса:

A = 1 — 1 1 3 2 — 5 2 1 — 3

1 — 1 1 0 5 — 8 0 3 — 5

1 — 1 1 0 5 — 8 0 0 — 1 5

R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.

Пусть в базисе вектор x → имеет координаты x

3 . Связь этих координат определяется уравнением:

3 e 1 ( 3 ) x 2 = x

3 e 2 ( 3 ) x 3 = x

Применим значения согласно условиям задачи:

Решим систему уравнений методом Крамера:

∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x

1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x

1 ∆ = — 1 — 1 = 1 ∆ x

2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x

2 ∆ = — 1 — 1 = 1 ∆ x

3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x

Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x

Ответ: x = ( 1 , 1 , 1 )