Решение линейных неравенств

Неравенства и их геометрическое содержание

Метод координат позволяет геометрически толковать не только уравнения, а так же и неравенства.

Потому как мы говорим, что уравнение с двумя переменными

Если выражение

и два линейные неравенства

Если коэффициенты

Выберем какую нибудь точку. подставим ее координаты в неравенство, что проверяется.

Если координаты точки удовлетворяют неравенству, то неравенство обозначает ту плоскость, в которой находится выбранная точка: если же координаты точки не удовлетворяют неравенство, то неравенство обозначает плоскость, которая не содержит выбранной точки.

Записать с помощью неравенства ту полуплоскость, в которой лежит точка

Решение. Подставим координаты точки

Студенту рекомендовано сделать рисунок и решить самостоятельно вторую часть примера.

Можно рассмотреть также систему неравенств:

Областью решения системы неравенств называется множество всех точек, координаты каждой из них удовлетворяют всем неравенствам системы.

пересечением нескольких множеств точек называется множество точек, каждая из которых принадлежим всем множествам, что пересекаются. Очевидно, областью решения системы неравенства служит пересечение областей решения каждой из неравенства системы.

Областью решений, системы линейных уравнений

является, очевидно пересечение полуплоскостей, что обозначается каждой из неравенств системы. Эта область может быть и пустым множеством, то есть множеством, которая не содержит ни одной точки.

Если же это множество точек не пустое, то она обозначается многоугольной областью. Если кроме того, эта область ограничена, то есть не содержит точек как и при большим значением координат, то ее называют началом многоугольника.

Записать с помощью системы неравенств множество точек, что лежат посередине треугольника с вершинами

Решение. Студенту рекомендовано выполнить рис., очевидно, множество всех внутренних точек треугольника

найдем неравенство, что обозначает первую из этих полуплоскостей. Сложим уравнение прямой

Подставляя в левую часть этого уравнения координаты точки

Аналогично, плоскость, что ограничена прямой

А плоскость, что ограничена прямой

Следует множество всех внутренних точек треугольника

Если вместо строгих неравенств (

Например, область решений неравенств:

является область, что ограничена треугольником

Аналогично интерпретируются геометрически линейные неравенства тремя переменными. Линейное неравенство с тремя неизвестными обозначается полуплоскость, а система таких неравенств — пересечение полупространства. Если он не пустой, является многогранной областью или в случае ограниченности многогранником.

Примеры решения задач:

Задача 2.121.

Построить область решений системы линейных неравенств:

Решение. Построим граничные прямые, что соответствуют данным неравенств, по двум точкам, что соответствуют этим прямым

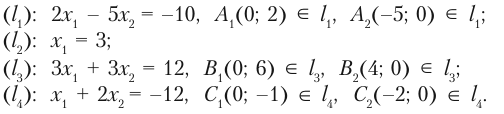
Каждая прямая делит плоскость на две полуплоскости. Та из них, что содержит начало координат и является областью решений каждой из неравенств. Стрелками обозначим полуплоскости, которые являются областями решений данных неравенств. Пересечение отмеченных полуплоскостей — четырехугольник

Задача 2.122 Построить область решений системы линейных неравенств:

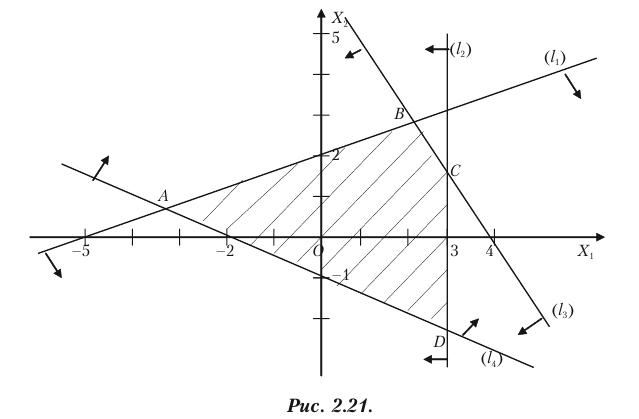
Решение. Построим граничные прямые, что соответствуют данным неравенствам:

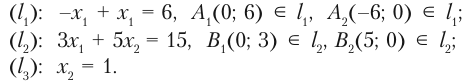
Область решение первой прямой содержит начало координат, а область решений второй и третьей неравенств — не содержат начало координат. Стрелками обозначим полуплоскости, точки которых удовлетворяют неравенствам. Областью решений является выпуклая неограниченная область (рис. 2.22).

Задача 2.123

Построить область решений системы линейных неравенств:

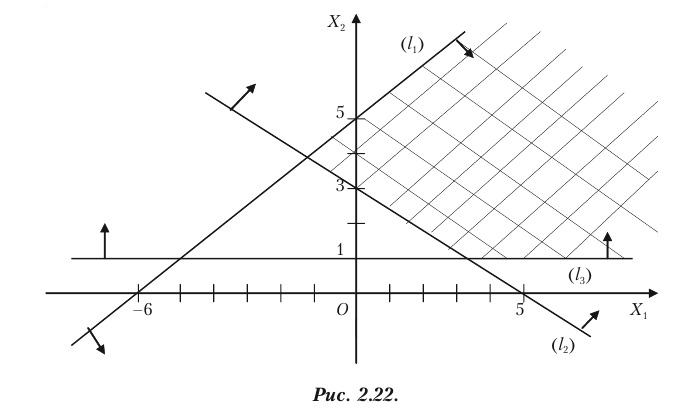
Решение. Строим граничные прямые:

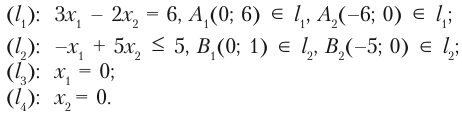
Строим область решений каждого неравенства (рис. 2.23).

Не существует ни одной точки для всех плоскостей, что соответствуют данным уравнениям. Следует, область решений пустая. Система неравенств несовместима.

Присылайте задания в любое время дня и ночи в ➔

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Тождественные преобразования неравенств.

Тождественные преобразования неравенств очень похожи на тождественные преобразования уравнений. Собственно, в этом и есть основная проблема. Отличия проскакивают мимо головы и… приехали.) Поэтому я особо выделю эти отличия. Итак, первое тождественное преобразование неравенств:

1. К обеим частям неравенства можно прибавить (отнять) одно и то же число, или выражение. Любое. Знак неравенства от этого не изменится.

На практике это правило применяется как перенос членов из левой части неравенства в правую (и наоборот) со сменой знака. Со сменой знака члена, а не неравенства! Правило один в один совпадает с правилом для уравнений. А вот следующие тождественные преобразования в неравенствах существенно отличается от таковых в уравнениях. Поэтому я выделяю их красным цветом:

2. Обе части неравенства можно умножить (разделить) на одно и то же
положительное
число. На любое
положительное
не изменится.

3. Обе части неравенства можно умножить (разделить) на одно и то же
отрицательное
число. На любое
отрицательное
число. Знак неравенства от этого
изменится на противоположный.

Вы помните (надеюсь…), что уравнение можно умножать/делить на что попало. И на любое число, и на выражение с иксом. Лишь бы не на ноль. Ему, уравнению, от этого ни жарко, ни холодно.) Не меняется оно. А вот неравенства более чувствительны к умножению/делению.

Наглядный пример на долгую память. Напишем неравенство, не вызывающее сомнений:

5 >
2

Умножим обе части на +3,
получим:

15 >
6

Возражения есть? Возражений нет.) А если умножим обе части исходного неравенства на -3,
получим:

15 >
-6

А это уже откровенная ложь.) Полное враньё! Обман народа! Но стоит изменить знак неравенства на противоположный, как всё становится на свои места:

15 -6

Про враньё и обман — это я не просто так ругаюсь.) «Забыл сменить знак неравенства…»
— это главная
ошибка в решении неравенств. Это пустяковое и несложное правило стольких людей ушибло! Которые забыли…) Вот и ругаюсь. Может, запомнится…)

Особо внимательные заметят, что неравенство нельзя умножать на выражение с иксом. Респект внимательным!) А почему нельзя? Ответ простой. Мы же не знаем знак этого выражения с иксом. Оно может быть положительное, отрицательное… Стало быть, мы не знаем, какой знак неравенства ставить после умножения. Менять его, или нет? Неизвестно. Разумеется, это ограничение (запрет умножения/деления неравенства на выражение с иксом) можно обойти. Если очень надо будет. Но это тема для других уроков.

Вот и все тождественные преобразования неравенств. Ещё раз напомню, что они работают для любых
неравенств. А теперь можно переходить к конкретным видам.

Неравенства, сводящиеся к линейным

Огромное количество неравенств с помощью равносильных преобразований можно заменить равносильным линейным неравенством, другими словами, свести к линейному неравенству. Такие неравенства называют неравенствами, сводящимися к линейным.

В школе почти одновременно с решением линейных неравенств рассматривают и несложные неравенства, сводящиеся к линейным. Они представляют собой частные случаи целых неравенств, а именно в их левой и правой части находятся целые выражения, которые представляют собой или линейные двучлены, или преобразуются к ним путем раскрытия скобок и приведения подобных слагаемых. Для наглядности приведем несколько примеров таких неравенств: 5−2·x>0, 7·(x−1)+3≤4·x−2+x, .

Неравенства, которые подобны по виду указанным выше, всегда можно свести к линейным. Это можно сделать путем раскрытия скобок, приведения подобных слагаемых, перестановки слагаемых местами и переноса слагаемых из одной части неравенства в другую с противоположным знаком.

Например, чтобы свести неравенство 5−2·x>0 к линейному, достаточно переставить слагаемые в его левой части местами, имеем −2·x+5>0. Для сведения второго неравенства 7·(x−1)+3≤4·x−2+x к линейному нужно немного больше действий: в левой части раскрываем скобки 7·x−7+3≤4·x−2+x, после этого приводим подобные слагаемые в обеих частях 7·x−4≤5·x−2, дальше переносим слагаемые из правой части в левую 7·x−4−5·x+2≤0, наконец, приводим подобные слагаемые в левой части 2·x−2≤0. Подобным образом и третье неравенство можно свести к линейному неравенству.

Из-за того, что подобные неравенства всегда можно свести к линейным, некоторые авторы даже называют их тоже линейными. Но все же будем их считать сводящимися к линейным.

Теперь становится понятно, почему подобные неравенства рассматривают вместе с линейными неравенствами. Да и принцип их решения абсолютно такой же: выполняя равносильные преобразования, их можно привести к элементарным неравенствам, представляющим собой искомые решения.

Чтобы решить неравенство подобного вида можно его предварительно свести к линейному, после чего решить это линейное неравенство. Но рациональнее и удобнее поступать так:

• после раскрытия скобок собрать все слагаемые с переменной в левой части неравенства, а все числа – в правой,
• после чего привести подобные слагаемые,
• а дальше – выполнить деление обеих частей полученного неравенства на коэффициент при x (если он, конечно, отличен от нуля). Это даст ответ.

Пример.

Решите неравенство 5·(x+3)+x≤6·(x−3)+1.

Решение.

Сначала раскроем скобки, в результате придем к неравенству 5·x+15+x≤6·x−18+1. Теперь приведем подобные слагаемые: 6·x+15≤6·x−17. Дальше переносим слагаемые с левую часть, получаем 6·x+15−6·x+17≤0, и снова приводим подобные слагаемые (что приводит нас к линейному неравенству 0·x+32≤0) и имеем 32≤0. Так мы пришли к неверному числовому неравенству, откуда делаем вывод, что исходное неравенство не имеет решений.

Ответ:

нет решений.

В заключение отметим, что существует и масса других неравенств, сводящихся к линейным неравенствам, или к неравенствам рассмотренного выше вида. Например, решение показательного неравенства 52·x−1≥1 сводится к решению линейного неравенства 2·x−1≥0. Но об этом будем говорить, разбирая решения неравенств соответствующего вида.

Список литературы.

• Алгебра: учеб. для 8 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
• Алгебра: 9 класс: учеб. для общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.
• Мордкович А. Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 11-е изд., стер. — М.: Мнемозина, 2009. — 215 с.: ил. ISBN 978-5-346-01155-2.
• Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 13-е изд., стер. — М.: Мнемозина, 2011. — 222 с.: ил. ISBN 978-5-346-01752-3.
• Мордкович А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. — 2-е изд., стер. — М.: Мнемозина, 2008. — 287 с.: ил. ISBN 978-5-346-01027-2.

Особенности решения двойных неравенств

Первой из них является его изображение на координатной оси. Использовать этот способ для простых неравенств нет необходимости. А вот в сложных случаях он может быть просто необходимым.

Для изображения неравенства нужно отметить на оси все точки, которые получились во время рассуждений. Это и недопустимые значения, которые обозначаются выколотыми точками, и значения из неравенств, получившиеся после преобразований

Здесь тоже важно правильно нарисовать точки. Если неравенство строгое, то есть , то эти значения выколотые. В нестрогих неравенствах точки нужно закрашивать

В нестрогих неравенствах точки нужно закрашивать.

Потом полагается обозначить смысл неравенств. Это можно сделать с помощью штриховки или дуг. Их пересечение укажет ответ.

Вторая особенность связана с его записью. Здесь предлагается два варианта. Первый — это окончательное неравенство. Второй — в виде промежутков. Вот с ним бывает, что возникают трудности. Ответ промежутками всегда выглядит как переменная со знаком принадлежности и скобок с числами. Иногда промежутков получается несколько, тогда между скобками нужно написать символ «и». Эти знаки выглядят так: ∈ и ∩. Скобки промежутков тоже играют свою роль. Круглая ставится тогда, когда точка исключена из ответа, а прямоугольная включает это значение. Знак бесконечности всегда стоит в круглой скобке.

Решение сложных линейных уравнений

Перейдем к более сложным уравнениям. Теперь конструкции станут сложнее и при выполнении различных преобразований возникнет квадратичная функция. Однако не стоит этого бояться, потому что если по замыслу автора мы решаем линейное уравнение, то в процессе преобразования все одночлены, содержащие квадратичную функцию, обязательно сократятся.

Пример №1

Очевидно, что первым делом нужно раскрыть скобки. Давайте это сделаем очень аккуратно:

Теперь займемся уединением:

Приводим подобные:

Очевидно, что у данного уравнения решений нет, поэтому в ответе так и запишем:

или корней нет.

Пример №2

Выполняем те же действия. Первый шаг:

Перенесем все, что с переменной, влево, а без нее — вправо:

Приводим подобные:

Очевидно, что данное линейное уравнение не имеет решения, поэтому так и запишем:

\,

либо корней нет.

Нюансы решения

Оба уравнения полностью решены. На примере этих двух выражений мы ещё раз убедились, что даже в самых простых линейных уравнениях всё может быть не так просто: корней может быть либо один, либо ни одного, либо бесконечно много. В нашем случае мы рассмотрели два уравнения, в обоих корней просто нет.

Но я бы хотел обратить ваше внимание на другой факт: как работать со скобками и как их раскрывать, если перед ними стоит знак «минус». Рассмотрим вот это выражение:

\

Прежде чем раскрывать, нужно перемножить всё на «икс»

Обратите внимание: умножается каждое отдельное слагаемое. Внутри стоит два слагаемых — соответственно, два слагаемых и умножается. И только после того, когда эти, казалось бы, элементарные, но очень важные и опасные преобразования выполнены, можно раскрывать скобку с точки зрения того, что после неё стоит знак «минус»

Да, да: только сейчас, когда преобразования выполнены, мы вспоминаем, что перед скобками стоит знак «минус», а это значит, что все, что в низ, просто меняет знаки. При этом сами скобки исчезают и, что самое главное, передний «минус» тоже исчезает

И только после того, когда эти, казалось бы, элементарные, но очень важные и опасные преобразования выполнены, можно раскрывать скобку с точки зрения того, что после неё стоит знак «минус». Да, да: только сейчас, когда преобразования выполнены, мы вспоминаем, что перед скобками стоит знак «минус», а это значит, что все, что в низ, просто меняет знаки. При этом сами скобки исчезают и, что самое главное, передний «минус» тоже исчезает.

Точно также мы поступаем и со вторым уравнением:

Я не случайно обращаю внимание на эти мелкие, казалось бы, незначительные факты. Потому что решение уравнений — это всегда последовательность элементарных преобразований, где неумение чётко и грамотно выполнять простые действия приводит к тому, что ученики старших классов приходят ко мне и вновь учатся решать вот такие простейшие уравнения. Разумеется, придёт день, и вы отточите эти навыки до автоматизма

Вам уже не придётся каждый раз выполнять столько преобразований, вы всё будете писать в одну строчку. Но пока вы только учитесь, нужно писать каждое действие отдельно

Разумеется, придёт день, и вы отточите эти навыки до автоматизма. Вам уже не придётся каждый раз выполнять столько преобразований, вы всё будете писать в одну строчку. Но пока вы только учитесь, нужно писать каждое действие отдельно.

Решение ещё более сложных линейных уравнений

То, что мы сейчас будем решать, уже сложно назвать простейшими задача, однако смысл остается тем же самым.

Задача №1

\

Давайте перемножим все элементы в первой части:

Давайте выполним уединение:

Приводим подобные:

Выполняем последний шаг:

\

Вот наш окончательный ответ. И, несмотря на то, что у нас в процессе решения возникали коэффициенты с квадратичной функцией, однако они взаимно уничтожились, что делает уравнение именно линейным, а не квадратным.

Задача №2

\

Давайте аккуратно выполним первый шаг: умножаем каждый элемент из первой скобки на каждый элемент из второй. Всего должно получиться четыре новых слагаемых после преобразований:

А теперь аккуратно выполним умножение в каждом слагаемом:

Перенесем слагаемые с «иксом» влево, а без — вправо:

\

Приводим подобные слагаемые:

Мы вновь получили окончательный ответ.

Нюансы решения

Важнейшее замечание по поводу этих двух уравнений состоит в следующем: как только мы начинаем умножать скобки, в которых находится более чем оно слагаемое, то выполняется это по следующему правилу: мы берем первое слагаемое из первой и перемножаем с каждым элементом со второй; затем берем второй элемент из первой и аналогично перемножаем с каждым элементом со второй. В итоге у нас получится четыре слагаемых.

Что такое линейное неравенство?

Для начала естественно определиться с тем, что же такое линейное неравенство с одной переменной. Другими словами, нужно узнать, как линейные неравенства выглядят в общем виде, чтобы можно было их отличать от других видов неравенств.

При просмотре школьных учебников по алгебре выяснилось, что определения разнятся, хотя и не принципиально. Приведем варианты определений линейного неравенства.

В учебнике Мордковича А. Г. для 9 классов приводится такое определение:

Определение.

Линейным неравенством с одной переменной x называют неравенство вида a·x+b>0, где вместо знака > естественно может быть любой другой знак неравенства (<, ≤, ≥), а a и b – действительные числа, причем a≠0.

В свою очередь в учебнике алгебры для 8 классов автора Макарычева Ю. Н. линейные неравенства определяются немного иначе:

Определение.

Неравенства вида a·x<c или a·x>c, где x – переменная, а a и c – некоторые числа, называются линейными неравенствами с одной переменной.

Здесь ничего не сказано о том, что коэффициент a при переменной x не может быть равен нулю, значит, допускается его равенство нулю, и неравенства вида 0·x>c и 0·x<c автор называет линейными. В этом определении также не упомянуты знаки нестрогих неравенств; с нашей точки зрения ничего ни мешает и неравенства a·x≤c, a·x≥c считать линейными.

Итак, главное различие между двумя этими определениями состоит в двух моментах:

• в форме записи (a·x+b>0 в первом, и a·x>c – во втором);
• и в допустимости равенства коэффициента a нулю (a≠0 — в первом, и a может быть равно нулю — во втором).

Первый момент не существенен в том плане, что неравенства a·x+b>0 и a·x>c являются , так как могут быть получены одно из другого переносом слагаемого из одной части в другую с противоположным знаком. Однако отдадим предпочтение первой записи, как мы это сделали и в разговоре о линейных уравнениях. Что же касается коэффициента при переменной, то на практике можно столкнуться, например, с неравенством 0·x+5>0, и так или иначе его придется решать, так что не будем отбрасывать случаи a=0.

Подведем итог нашим рассуждениям: чтобы у нас в дальнейшем не возникало разногласий, давайте условимся считать линейными неравенствами в одной переменной x неравенства вида a·x+b<0, a·x+b>0, a·x+b≤0 и a·x+b≥0, где a и b могут быть любыми действительными числами. Понятно, что переменная может быть обозначена не только буквой x, но и любой другой буквой.

Согласно нашей договоренности, неравенства 4·x−1>0, 0·z+2,3≤0, — это примеры линейных неравенств. А вот неравенства 5·x>7, −0,5·y≤−1,2 и т.п. мы будем называть неравенствами, сводящимися к линейным. Здесь же отметим, что масса других неравенств могут сводиться к линейным неравенствам, о них мы еще скажем в .

Шаг 2: Найти допустимый интервал значений неизвестной

Когда мы решаем линейное неравенство с одним неизвестным, один из ключевых этапов — это определение допустимого интервала значений этой неизвестной. Именно в этом интервале будут находиться все значения, которые удовлетворяют данному неравенству.

Допустимый интервал значений неизвестной можно найти, анализируя знак неравенства и коэффициенты в уравнении. Во-первых, нужно понять, какое условие на значение неизвестной накладывает неравенство: больше, меньше или больше либо равно/меньше либо равно. Во-вторых, если в уравнении есть коэффициент при неизвестной, нужно учесть его знак и его значение.

Если знак неравенства:

• Больше (>): для нахождения интервала значений необходимо поделить обе части неравенства на коэффициент при неизвестной. Результатом будет условие на ее значение в виде: неизвестная > некоторое число.
• Меньше (
• Больше либо равно (≥): для нахождения интервала значений нужно также поделить обе части неравенства на коэффициент при неизвестной, однако для определения интервала нужно учесть знак этого коэффициента. Если коэффициент положителен, результатом будет условие на значение неизвестной в виде: неизвестная >= некоторое число. Если коэффициент отрицателен, результатом будет условие на значение неизвестной в виде: неизвестная <= некоторое число.
• Меньше либо равно (≤): для нахождения интервала значений необходимо также поделить обе части неравенства на коэффициент при неизвестной, но в этом случае нужно учесть знак этого коэффициента. Если коэффициент положителен, результатом будет условие на значение неизвестной в виде: неизвестная <= некоторое число. Если коэффициент отрицателен, результатом будет условие на значение неизвестной в виде: неизвестная >= некоторое число.

Итак, после определения условия на значение неизвестной, мы получим допустимый интервал значений, в котором могут находиться корни данного линейного неравенства.

Пример:

Рассмотрим линейное неравенство: 2x — 3 ≥ 7.

Исходя из знака неравенства «≥», мы делим обе части неравенства на коэффициент при неизвестной «2».

Получим: x — 3/2 ≥ 7/2.

Здесь условие на значение неизвестной выглядит так: x ≥ 7/2 + 3/2 = 10/2.

Итак, допустимый интервал значений для этого линейного неравенства — это все значения неизвестной x, которые больше или равны 10/2.

Графическое представление

Графическое представление уравнения и неравенства имеет существенные отличия. Когда мы графически представляем уравнение, мы ищем точки, в которых прямая пересекает ось x. Количество корней уравнения может быть равно или меньше числа переменных. Например, уравнение y = x^2 — 4x + 3 имеет два корня, так как это квадратное уравнение.

Неравенство представляет условия или ограничения для переменных. Точки, удовлетворяющие этим условиям, могут быть связаны между собой общей областью на графике. То есть, график неравенства может быть как линия, так и областью. Например, y

Еще одно отличие между графическим представлением уравнения и неравенства заключается в том, что точки пересечения прямой и оси x для уравнения являются решениями уравнения, в то время как точки на графике для неравенства являются значениями переменной, удовлетворяющим условию неравенства. Например, для y ≤ x + 2 все точки на и под диагональной линией являются решением неравенства.

Что такое линейное уравнение с одной переменной

Рассмотреть понятие линейного уравнения можно на образце задачи. Предположим, что нужно определить такие численные значения переменной х, при которых соответственные значения выражений 3х и х+8 будут одинаковыми. Для этого необходимо решить уравнение:

3х=х+8

Если х=4, правая и левая части уравнения будут равны. В данном случае число 4 является решением или корнем рассматриваемого уравнения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Определение

Корень уравнения с одной переменной является числом, благодаря которому данное уравнение становится верным равенством.

Решить уравнение в алгебре — значит определить множество всех его корней.

Линейным уравнением является любое алгебраическое уравнение, обладающее одним неизвестным, степень которого равна единице.

Общий вид линейного уравнения можно записать, таким образом:

kx+b=0

Где k и b — являются произвольными числами.

Примеры линейных уравнений:

1. Уравнение x+5=8 обладает одним корнем 3. Уникальность корня объясняется тем, что при x<3 левая часть уравнения будет меньше 8, а при x>3 больше 8.
2. Уравнение (x+2)(x-1)(x-7)=0 включает три корня: -2, 1 и 7. Каждый корень при подстановке в выражение превращает его в справедливое равенство. Когда х равен любому другому числу, ни один из множителей (а значит, и их произведение) не равен нулю.
3. Уравнение x+3=x-1 не обладает корнями, так как при любых x значение выражения, стоящего в левой части уравнения, на 4 больше соответственного значения выражения, которое расположено в правой части. Множество корней будет пустым.
4. Уравнение x=|x| обладает бесконечным множеством корней. Какое-либо число, больше нуля, или ноль может стать его корнем.
5. Уравнение 5(x+8)=40+5x обладает бесконечным множеством корней. При этом любое значение х — корень уравнения, в связи с тем, что выражения 5(x+8) и 40+5x тождественно равны. Данное уравнение удовлетворяется тождественно.

Перечисленные уравнения обладают общей формой:

\(kx+b=0 \Leftrightarrow kx=-b\)

Рассматриваемые выражения по внешнему виду схожи друг с другом. Значение х является переменной или неизвестным, k и b — представляют собой произвольные числа.

Уравнения, которые не соответствуют этой записи, не являются линейными, к примеру:

\(x^{2}-1=0\)

(x-3)(x+5)=0

\(\left | x \right |=2\)

Как записать ответ неравенства

В этом уроке мы не будем разбирать, как решаются линейные или квадратные неравенства. Нас будет интересовать только вопрос: «Как записать ответ неравенства специальными математическими знаками, например, в виде x ∈ (3; +∞) ?».

Стоит отметить, что далеко не во всех учебных заведениях требуют обязательно записывать ответ неравенства в виде x ∈ (3; +∞) . В некоторых школах в 8 и 9 классе разрешают оставлять ответ, используя знаки больше « > » и « ». Например, следующим образом.

Впрочем, мы рекомендуем освоить запись ответа неравенства в математических обозначениях сразу, так как в любом случае в старшей школе и затем в университете будут требовать именно такую запись ответа.

Перед разбором, как записывать ответ неравенства математическими знаками, вспомним расшифровку и обозначение этих знаков.

Знак	Расшифровка
∈	«Принадлежит» Легко запомнить знак, как зеркальное отображение русской буквы « Э » или как символ евро « € », но только с одной палочкой посередине.
( … )	«Круглые скобки» Используются, когда число на границе интервала НЕ входит в сам интервал. На числовой оси такие числа обозначают «пустой» точкой.
	«Квадратные скобки» Используются, когда число на границе интервала входит в сам интервал. На числовой оси такие числа обозначают «заполненной» точкой.
∪	«Объединение» Знак похож на подковку. Используется для объединения двух и более интервалов.
+ ∞	«Плюс бесконечность» Изображается как цифра « 8 » на боку со знаком « + » слева. Обозначает бесконечность на положительном (правом) краю числовой оси.
− ∞	«Минус бесконечность» Изображается как цифра « 8 » на боку со знаком « − » слева. Обозначает бесконечность на отрицательном (левом) краю числовой оси.

Перейдем к непосредственной записи ответа неравенства. Рассмотрим и решим линейное неравенство.

Мы решили линейное неравенство, теперь запишем его ответ с помощью математических знаков.

Перед тем, как записывать ответ неравенства, обязательно изобразите его на числовой оси.

Итак, мы изобразили ответ неравенства на числовой оси. После этого запишем слово «Ответ:» и за ним запишем « x ∈ ». Такая запись читается как «икс принадлежит».

Взглянув на рисунок ответа на числовой оси, мы видим, что область решений начинается с числа « 14 ». Число « 14 » не входит в область решений («пустая» точка на оси). Значит, используем круглую скобку.

Нам остается понять, где заканчивается область решений справа. Правильный ответ — справа область заканчивается в положительной бесконечности « + ∞ ».

На числовой оси на обоях краях слева и справа соответственно расположены «минус» и «плюс» бесконечности. Как правило, их не рисуют на числовой оси лишний раз, т.к. их наличие на оси подразумевается.

Запишем окончательный ответ.

Знаки « + ∞ » и « − ∞ » всегда записываются с круглыми скобками.

Также как и в предыдущем примере всегда начинаем записывать ответ с записи « x ∈… ».

В ответе « x ≤ 8 » область решений начинается с « − ∞ » и заканчивается на « 8 », которое входит в ответ. Значит, « 8 » будет с квадратной скобкой. Так и запишем в ответе.

Запись ответа неравенства для квадратных неравенств

При решении квадратных неравенств часто может получаться несколько интервалов в ответе. Разберемся, как их записывать в ответ. Рассмотрим пример квадратного неравенства и его решение.

x 2 − 3x + 2 3 2 − 4 · 1 · 2

2 · 1

Рассмотрим другой пример квадратного неравенства и его решения.

x_1;2 =

2 ± √ 2 2 − 4 · 1 · (−3)

2 · 1

В ответе неравенства мы получили два интервала в области решений (x ≤ −1; x ≥ 3) и оба интервала нужно записать в ответ. Запись ответа неравенства всегда делается слева направо (как мы привыкли читать).

Начнем слева направо записывать интервалы в ответ. Первый интервал начинается с «минус» бесконечности и заканчивается на « −1 » (включительно). Так и запишем.

Второй интервал начинается с « 2 »(включительно) и заканчивается на «плюс» бесконечности. Для объединения интервалов используем знак « ∪ » («объединение»).

Виды уравнений с одной переменной

Существуют разные алгебраические уравнения. Наиболее распространенными из них являются:

• линейные;
• квадратные.

Линейные уравнения записывают в виде:

ах + b = 0

Где a и b — являются действительными числами.

В решении линейных уравнений удобно применять следующие свойства:        

• в том случае, когда а не равно нулю, уравнение обладает единственным корнем: х = -b : а;
• при нулевом значении, а уравнение не имеет корней;
• когда а и b равны нулю, корень уравнения является любым числом.

Квадратное уравнение имеет следующий вид:

ax2 + bx + c = 0,

Где коэффициенты a, b и c — являются произвольными числами, a обладает ненулевым значением.          

Применение онлайн-калькуляторов

Во всемирной сети существуют сервисы, позволяющие вычислять линейные уравнения буквально в течение нескольких секунд. С их помощью решить неравенство любой сложности сможет даже пользователь, совершенно не понимающий методы, используемые для нахождения ответов.

Эти порталы привлекательны ещё и тем, что каждый выполненный шаг при решении подробно описывается. Появление ошибки при расчёте невозможно. Поэтому эти сайты востребованы даже у математиков, рассчитывающих целые и дробные выражения.

Чтобы получить ответ, регистрироваться не нужно. Необходимо просто зайти на сайт с помощью веб-обозревателя и указать заданное неравенство. Как только искомое выражение будет вписано, следует кликнуть по меню «Рассчитать» и получить ответ с пошаговым решением.

Дробно-рациональные неравенства

До сих пор мы рассматривали целые нер-ва. Однако, по аналогии с уравнениями, существуют ещё и дробно-рациональные нер-ва. В них выражение с переменной может стоять в знаменателе. Приведем примеры дробно-рациональных нер-в:

Любое такое нер-во можно представить в виде

где Р(х) и Q(х) – некоторые многочлены. Естественно, вместо знака «>» может стоять и другой знак. Для примера преобразуем к такому виду нер-во

Перенесем все слагаемые влево:

Далее приведем левую часть к общему знаменателю:

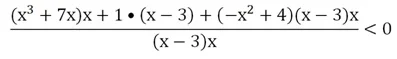
Осталось раскрыть скобки:

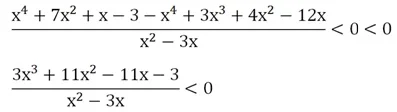
В итоге и в числителе, и в знаменателе стоят многочлены.

Рассмотрим нер-ва

а/b>0 и ab> 0

Докажем, что они равносильны друг другу. Возможны 5 случаев:

1. И а, и b являются положительными числами. Тогда оба нер-ва верны, ведь и произведение, и отношение двух положительных чисел само положительно:

10•5 = 50 > 0

10/5 = 2 > 0

2. Оба числа, а и b, отрицательны, тогда снова оба нер-ва справедливы, ведь при умножении и делении двух отрицательных чисел получается положительное число. Например:

(– 10)•(– 5) = 50 > 0

(– 10)/(– 5) = 2 > 0

3. Только одно из чисел положительно, а другое отрицательно, тогда их произведение, как и частное, меньше нуля, и нер-ва неверны:

(– 10)•5 = – 50< 0

(– 10):5 = – 2 < 0

4. Число a равно нулю. Тогда выражения ab и a/b также равны нулю, а потому рассматриваемые нер-ва неверны:

0•5 = 0

0/5 = 0

5. Число b равно нулю. Тогда произведение ab равно нулю, а дробь а/b не имеет смысла (из-за нуля в знаменателе). То есть нер-ва а/b> 0 и ab> 0 снова одновременно неверны.

Получили, что при любых значениях а и b нер-ва а/b> 0 и ab> 0 либо одновременно справедливы, либо одновременно несправедливы. Это значит, что они равносильны.

Это значит, что от дробно-рационального нер-ва можно перейти к равносильному ему целому нер-ву.

Пример. Решите нер-во

Решение:

Исходному нер-ву равносильно иное нер-во:

(х – 1)(х – 2)(х – 3)(х – 4)> 0

Решим его методом интервалов:

Получаем, что х∊(1; 2)∪(3; 4).

Ответ: (1; 2)∪(3; 4).

Пример. Решите нер-во

Решение. В числителе и знаменателе находятся квадратные трехчлены. Их можно разложить на корни, если знать их корни. Найдем их.

х2 – 9х + 14 = 0

D = b2– 4ас = (– 9)2 – 4•1•14 = 84 – 56 = 25

х₁ = (9 – 5)/2 = 2

х₂ = (9 + 5)/2 = 7

Так как корни равны 2 и 7, то можно записать, что

х2 – 9х + 14 = (х – 2)(х – 7)

Аналогично разложим знаменатель

х2 – 14х + 45 = 0

D = b2– 4ас = (– 14)2 – 4•1•45 = 196 – 180 = 16

х₁ = (14 – 4)/2 = 5

х₂ = (14 + 4)/2 = 9

х2 – 14х + 45 = (х – 5)(х – 9)

Перепишем исходное нер-во:

Ему равносильно другое нер-во:

(х – 2)(х – 7)(х – 5)(х – 9) > 0

Его можно решить методом интервалов:

Получаем, что х∊(– ∞; 2)∪(5; 7)∪(9; + ∞).

Ответ: х∊(– ∞; 2)∪(5; 7)∪(9; + ∞).

Обратим внимание на одну особенность метода интервала в случаях, когда решается дробно-рациональное нер-во. Она касается нестрогих нер-в (со знаками «≤» и «≥»)

В целых нестрогих нер-вах сами точки, при которых выражение слева обращается в ноль, включаются в решение

Но при рассмотрении дроби важно понимать, что ее знаменатель не может быть равным нулю. Поэтому при нестрогом нер-ве в ответ надо включить точки, обращающие в ноль числитель, но при этом исключить точки, обращающие в ноль знаменатель

Пример. Решите нер-во

Числитель обращается в ноль в точках (– 2) и 4, а знаменатель – в точках (– 7) и 8. Так как нер-во нестрогое, то числа 4 и (– 2) будут входить в решение (на координатной прямой мы отметим их закрашенным кружочком), а числа (– 7) и 8 – нет (их отметим как «выколотые точки»):

В итоге получаем, что дробь неотрицательна при х∊(– ∞; – 7)∪∪(8; – ∞).

Ответ: (– ∞; – 7)∪∪(8; – ∞).