Способы нахождения площади
Но существуют также и другие способы, по которым можно найти S этого многоугольника. Рассмотрим основные из них.
Через две стороны и угол
Если вам известны две стороны любого треугольника и угол между ними, найти площадь можно по формуле:
\(S=\frac12a\times b\times\sin\alpha\)
где a и b — стороны фигуры, а α — угол между ними.
Через радиус описанной окружности и три стороны
Если вам известен радиус окружности, которая описана вокруг вашего треугольника, а также все его стороны, можно вычислить S следующим образом:
\(S=\frac{a\times b\times c}{4\times R}\)
где a, b и c — стороны фигуры, а R — радиус описанной окружности.
Через радиус вписанной окружности и три стороны
В случае, если вам известны все три стороны и радиус вписанной в треугольник окружности, можно найти его площадь по формуле:
\(S=r\times\frac{a+b+c}2\)
где r — радиус вписанной окружности, \(\frac{a+b+c}2\) — полупериметр фигуры.
Таким образом, формулу можно выразить всего двумя множителями:
\(S=r\times p\)
где p — полупериметр треугольника.
Через сторону и два угла
Если в данной фигуры вам известна лишь одна сторона и две прилегающих к ней угла, ее S можно найти следующим образом:
\(S=\frac12\times a^2\times\frac{\sin\alpha\times\sin\beta}{\sin\gamma}\)
причем \(\gamma=180^\circ-(\alpha+\beta)\)
Для прямоугольного треугольника
В случае треугольника с прямым углом формулы для нахождения площади будут немного отличаться. Найти S можно будет несколькими способами.
По двум сторонам
Если вам известны оба катета данной фигуры, рассчитать S можно умножив их друг на друга, а потом разделив на пополам:
\(S=\frac{a\times b}2\)
где a и b — катеты прямоугольного треугольника.
Через гипотенузу и острый угол
Зная длину гипотенузы и величину одного из острых углов, мы можем найти один из его катетов по определению косинуса. И уже потом можем использовать формулу для нахождения площади треугольника через две стороны и синус угла между ними.
Начнем с поиска катета:
\(\cos\left(\alpha\right)=\frac ac\)
\(a=c\times\cos\left(\alpha\right)\)
где c — гипотенуза треугольника, a — его катет, а α —угол между ними.
Подставляем получившееся значение в формулу \(S=\frac12a\times c\times\sin\alpha\), получается:
\(S=c^2\times\cos\left(\alpha\right)\times\sin\left(\alpha\right)\)
Через катет и прилежащий угол
В этом случае нужно будет использовать следующую формулу:
\(S=\frac12\times a^2\times\tan\left(\alpha\right)\)
Через радиус вписанной окружности и гипотенузу
Зная радиус вписанной в данную фигуру окружности и гипотенузу, мы можем использовать следующее уравнение для расчета:
\(S=r\times(r+c)\)
где r — радиус вписанной окружности, c — гипотенуза.
Через вписанную окружность
Радиус, опущенный в точку касания окружности и гипотенузы прямоугольного треугольника, делит эту гипотенузу на неравные отрезки. Если нам известны величины этих отрезков, мы можем найти площадь фигуры по формуле:
\(S=с_1\times с_2\)
где \(с_1\) и \(с_2\) — неравные отрезки гипотенузы.
По формуле Герона
Если мы знаем длины всех сторон данного многоугольника, мы можем рассчитать S по формуле Герона:
\(S=(p-a)\times(p-b)\)
где \(p=\frac{a+b+c}2\) — полупериметр фигуры.
По стороне и высоте
Данная формула является универсальной для нахождения площади, рассматриваемой нами фигуры. Для этого достаточно знать длину стороны и длину проведенной к ней высоты. Сама формула (половина произведения основания на высоту) выглядит следующим образом:
где A — сторона данного треугольника, а H — высота треугольника.
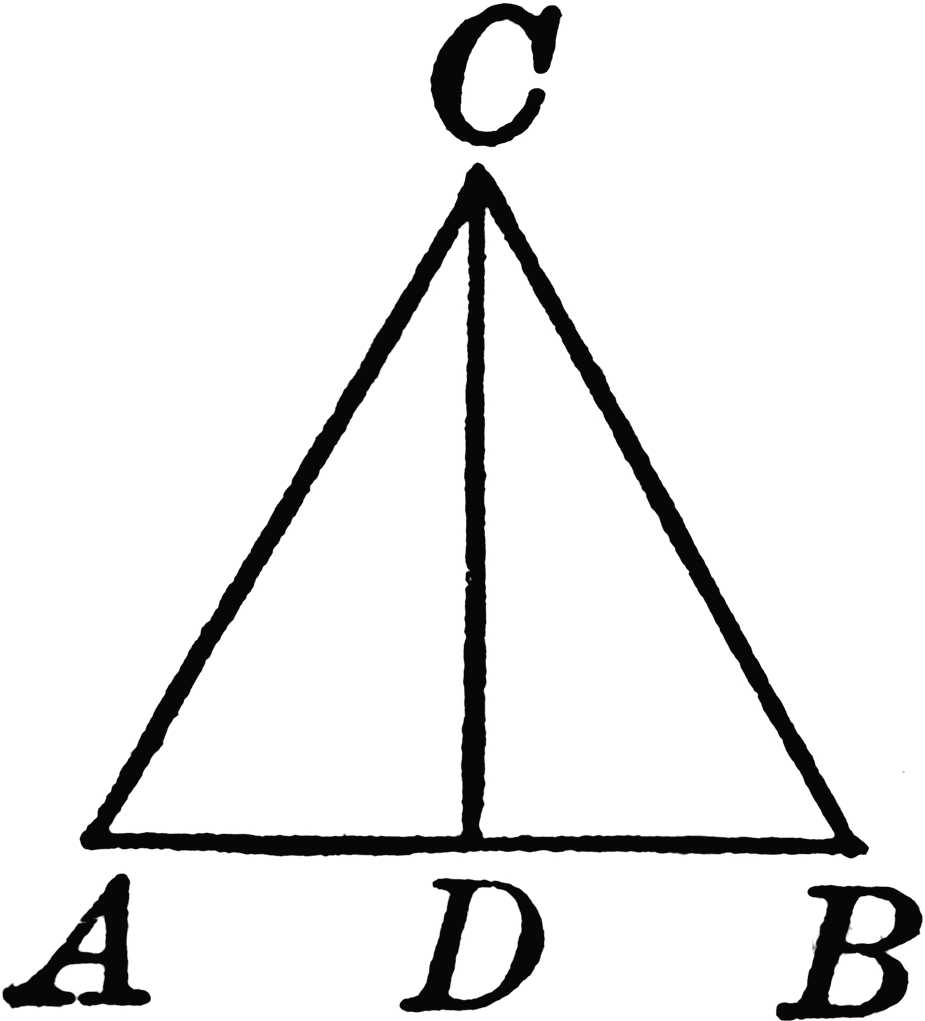
Например, чтобы найти площадь остроугольного треугольника ACB, нужно умножить его сторону AB на высоту CD и разделить получившееся значение на два.
Однако не всегда бывает легко найти площадь треугольника таким способом. Например, чтобы воспользоваться этой формулой для тупоугольного треугольника, необходимо продолжить одну из его сторон и только после этого провести к ней высоту.
На практике данная формула применяется чаще остальных.
Площади треугольников со специфическими свойствами
Как найти площадь прямоугольного треугольника? Особенностью этой фигуры является то, что две ее стороны одновременно являются ее высотами. Если а и b являются катетами, а с становится гипотенузой, то площадь находим так:
Как найти площадь равнобедренного треугольника? В нем две стороны с длиной а и одна сторона с длиной b. Следовательно, его площадь определить можно путем деления на 2 произведения квадрата стороны а на синус угла γ.
Как найти площадь равностороннего треугольника? В нем длина всех сторон равняется а, а величина всех углов — α. Его высота равна половине произведения длины стороны а на корень квадратный из 3. Чтобы найти площадь правильного треугольника, нужно квадрат стороны а умножить на корень квадратный из 3 и разделить на 4.
Треугольник — это одна из самых распространенных геометрических фигур, с которой мы знакомимся уже в начальной школе. С вопросом, как найти площадь треугольника, сталкивается каждый школьник на уроках геометрии. Так, какие же особенности нахождения площади данной фигуры можно выделить? В данной статье мы рассмотрим основные формулы, необходимые для выполнения такого задания, а также разберем виды треугольников.
По стороне и высоте
Данная формула является универсальной для нахождения площади, рассматриваемой нами фигуры. Для этого достаточно знать длину стороны и длину проведенной к ней высоты. Сама формула (половина произведения основания на высоту) выглядит следующим образом:
где A — сторона данного треугольника, а H — высота треугольника.

Например, чтобы найти площадь остроугольного треугольника ACB, нужно умножить его сторону AB на высоту CD и разделить получившееся значение на два.
Однако не всегда бывает легко найти площадь треугольника таким способом. Например, чтобы воспользоваться этой формулой для тупоугольного треугольника, необходимо продолжить одну из его сторон и только после этого провести к ней высоту.
На практике данная формула применяется чаще остальных.
8 класс. Геометрия. Площадь. Площадь треугольника и трапеции. — Площадь треугольника.
Комментарии
Формула для площади треугольника и следствия из неё
На данном уроке мы докажем формулу для площади треугольника и решим несколько задач на её применение.
Будем называть сторону – основанием, тогда – высота, опущенная к этой стороне (см.
Рис. 1. Высота и основание
Теорема о свойстве медианы треугольника
Площадь треугольника равна половине произведения его основания на высоту.
В формульном виде: .
Доказательство:
Рис. 2. Иллюстрация к теореме
Достроим треугольник до параллелограмма – см. Рис. 2.
(по трём сторонам: – общая, , – как противоположные стороны параллелограмма).
Из равенства треугольников следует равенство их площадей: . Получаем: . Воспользовавшись формулой для площади параллелограмма: .
Доказано.
Сформулируем несколько следствий из данной теоремы.
Следствие 1
Площадь прямоугольного треугольника равна половине произведения его катетов (см. Рис. 3).
Рис. 3. Иллюстрация к следствию 1
Следствие 2
Если высоты двух треугольников равны, то их площади относятся как основания (см. Рис. 4).
Рис.
Теорема 2
Медиана треугольника разбивает его на два равновеликих треугольника (см. Рис. 5).
Доказательство:
Рис. 5. Иллюстрация к теореме
Пусть – треугольник, – медиана, – высота. Для треугольников – также является высотой. Запишем формулу для площади каждого из этих треугольников: , . Так как ( – медиана), то: . Значит, эти треугольники являются равновеликими.
Доказано.
Формула для площади ромба
Теорема 3
Площадь ромба равна половине произведения его диагоналей (см. Рис. 6).
В виде формулы: .
Доказательство:
Рис. 6. Иллюстрация к теореме
(по 3 сторонам: – общая, – свойства ромба). Из равенства треугольников следует равенство их площадей. Значит: . Но формулу для площади треугольника мы уже знаем: (т. к. , поэтому – высота треугольника ). Получаем следующее равенство: ( – свойство диагоналей ромба).
Доказано.
Свойство треугольников с равными углами
Теорема 4
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
В виде формулы: .
Доказательство:
Рис. 7. Иллюстрация к теореме
Совместим треугольники так, чтобы вершина совпала с вершиной , сторона лежала на прямой , а сторона лежала на прямой .
Рис. 8. Иллюстрация к теореме
Рассмотрим отношение площадей треугольников и . Эти треугольники имеют общую высоту, проведённую из вершины , поэтому, по следствию 2 из теоремы 1, их площади относятся как основания, то есть: .
Из аналогичных соображений: . Перемножив эти два равенства, получим: .
Доказано.
Задачи на площадь треугольника и следствия из неё
Теперь решим несколько задач, используя доказанные формулы и свойства.
Задача 1
Площадь прямоугольного треугольника равна . Найдите катеты этого треугольника, если известно, что один из них составляет другого.
Решение
Пусть один из катетов равен , а второй – . Тогда площадь треугольника можно вычислить по формуле: . Но, по условию: . Подставив это выражение, получаем: . Откуда: .
Ответ: .
Задача 2
В треугольнике точка лежит на стороне , точка лежит на стороне . Кроме того: , , . Чему равна площадь треугольника (Рис. 9)?
Решение:
Рис. 9. Иллюстрация к задаче
Воспользуемся теоремой 4 для треугольников и ( – общий угол этих треугольников). Из этой теоремы следует, что: . Значит: .
Ответ: .
На этом уроке мы рассмотрели понятия площадей треугольника и ромба, вывели из них некоторые следствия. На следующем уроке мы научимся вычислять площадь трапеции.
ИСТОЧНИК
http://x-uni.
https://www.youtube.com/watch?v=2e7Qf6iEPPs
https://www.youtube.com/watch?v=mCI3Yj4t1O8
http://v.5klass.net/zip/7b9fd7f7274ef33da70777cf1fd1d25d.zip
http://fs01.metod-kopilka.ru/files/2015/01/11/Ploschad_treugolnika_8_klassna_18_noyabrya_pptx_1421009203.pptx
http://5klass.net/datas/geometrija/Ploschad-treugolnika-8-klass/0004-004-Ploschad-treugolnika.jpg
http://www.klassnye-chasy.ru/userfiles/ploshchad-treugolnika1.jpg
http://fs00.infourok.ru/images/doc/309/308291/img18.jpg
Окружности
Другой способ, с помощью которого можно найти площадь треугольника, предусматривает использование вписанных и описанных окружностей. Чтобы получить необходимую нам величину с помощью вписанной окружности, нам потребуется узнать её радиус. Обозначим его «r». Тогда формула, по которой мы будем проводить вычисления, примет следующий вид: S=r*P, где P — это половина от суммы длин всех сторон.
В прямоугольном треугольнике эта формула немного преобразуется. Конечно, вы можете использовать и указанную выше, однако лучше взять для вычислений другое выражение. S=E*W, где E и W — это длины отрезков, на которые делится гипотенуза, точкой касания окружности.
Говоря об описанной окружности, найти площадь треугольника, также не составит труда. Введя обозначение R, как радиус описанной окружности, можно получить следующую формулу, необходимую для вычисления искомой величины: S= (M*N*L):(4*R). Где три первые величины — это стороны треугольника.
Говоря о равностороннем треугольнике, за счет ряда простейших математических преобразований можно получить немого изменённые формулы:
S=(3 1/2 *M 2)/4;
S=(3*3 1/2 *R 2)/4;
S=3*3 1/2 *r 2 .
Во всяком случае, любая формула, позволяющая найти площадь треугольника, может быть изменена в соответствии с данными поставленной задачи. Так что все написанные выражения не являются абсолютами. При решении задач поразмышляйте, чтобы найти наиболее подходящий способ решения.
Площадь равностороннего треугольника через сторону, формула
Учитывая названные свойства треугольника с равными сторонами, высчитать его площадь можно несколькими способами:
- через длину стороны:
- через высоту;
- используя треугольник, вписанный в окружность.
Чтобы понять формулы для вычисления, рассмотрим рисунок:
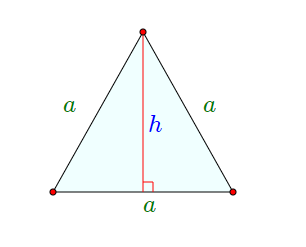
На данном рисунке условные обозначения следующие:

Чтобы находить площадь равностороннего треугольника через его сторону, можно использовать формулу:
Высота h, являющаяся одновременно биссектрисой и медианой, делит нижнюю сторону на две половины. Длину одной половину можно выразить \(a/2\).
Кроме этого, она образует два прямоугольных треугольника, один из которых рассмотрим отдельно:
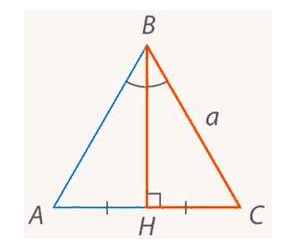
Используя теорему Пифагора, получаем равенство:
Из приведенных выражений легко вывести формулу для нахождения площади, если известна длина стороны:
Доказательство данной формулы настолько очевидно, что может быть легко восстановлено в памяти в любой момент.
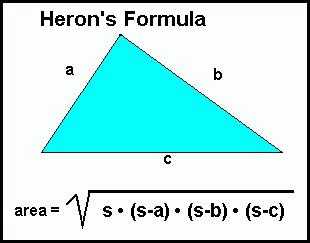
Формула Герона
Кроме всех прочих ответов на вопрос о том, как вычислить площадь треугольника, есть формула, позволяющая получить необходимое нам значение, зная исключительно длины сторон. То есть, если нам известны длины всех сторон, то нам нет необходимости проводить высоту и вычислять её длину. Мы можем воспользоваться, так называемой формулой Герона.
Если M, N, L — это длины сторон, тогда мы можем найти площадь треугольника, следующим образом. P=(M+N+L)/2, тогда необходимая нам величина S 2 =P*(P-M)*(P-L)*(P-N). В итоге, нам останется только вычислить корень.
Для прямоугольного треугольника формула Герона немного упрощается. Если M, L -это катеты, тогда S=(P-M)*(P-L).
Правильный и равнобедренный треугольники
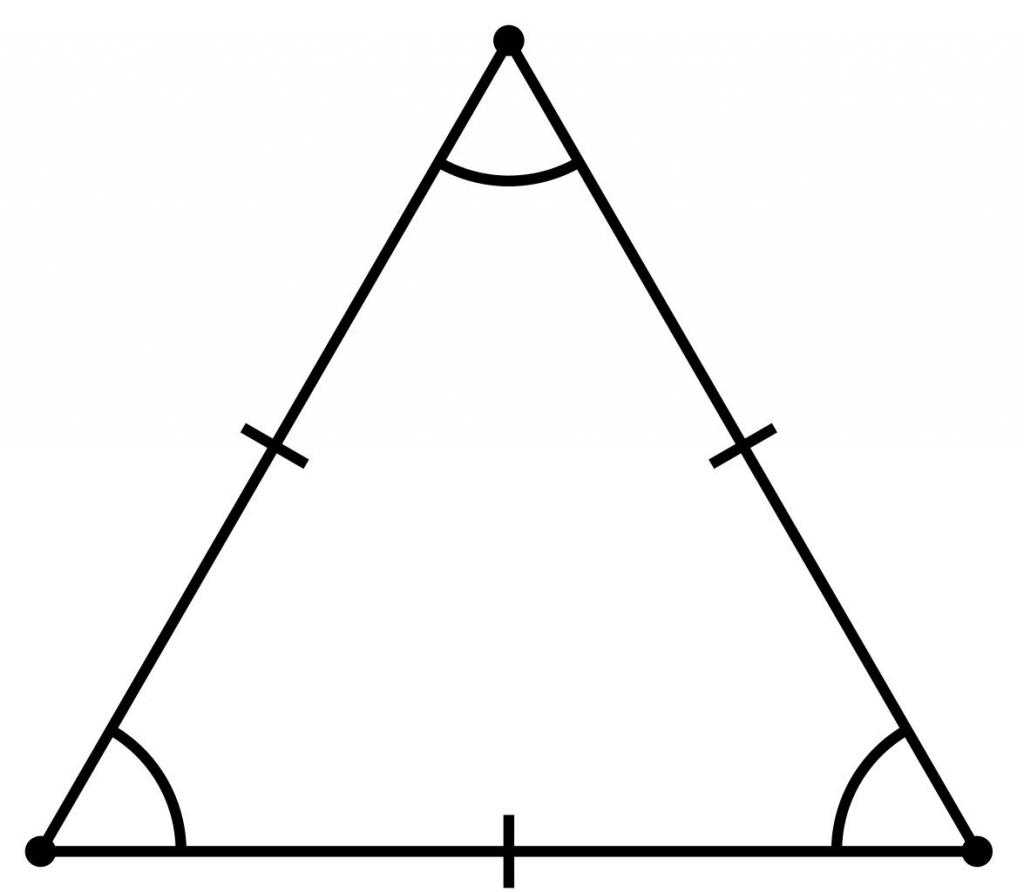
Правильным многоугольником называется фигура, включающаяся в себя n углов, у которой все стороны и углы равны. Таким и является правильный треугольник. Так как сумма всех углов треугольника составляет 180°, то каждый из трех углов равен 60°.
Правильный треугольник, благодаря его свойству, также называют равносторонней фигурой.
Стоит также отметить, что в правильный треугольник можно вписать только одну окружность и около него можно описать только одну окружность, причем их центры расположены в одной точке.

Помимо равностороннего типа, можно также выделить равнобедренный треугольник, несильно от него отличающийся. В таком треугольнике две стороны и два угла равны между собой, а третья сторона (к которой прилегают равные углы) является основанием.
На рисунке показан равнобедренный треугольник DEF, углы D и F которого равны, а DF является основанием.
Площадь треугольника формула

*То есть если нам будет известна любая сторона треугольника и высота опущенная на эту сторону, то мы всегда сможем вычислить площадь этого треугольника.
Формула вторая
Как уже было изложено в статье о площади параллелограмма формула имеет вид:
Площадь треугольника равна половине его площади, значит:
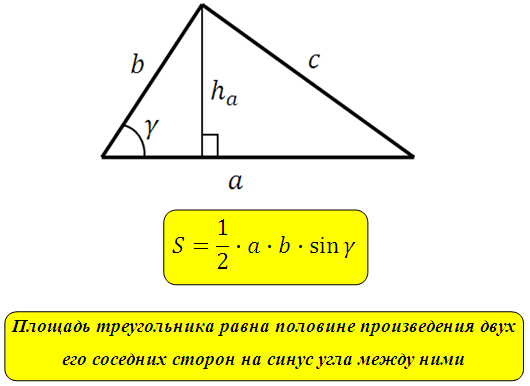
*То есть если будут известны любые две стороны в треугольнике и угол между ними, мы всегда сможем вычислить площадь такого треугольника.
Формула Герона (третья)
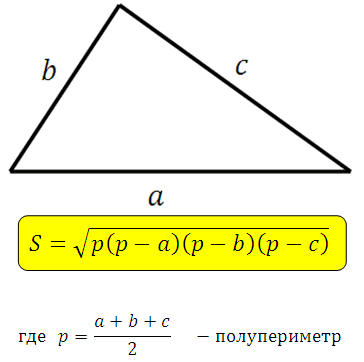
Данную формулу выводить сложно и вам это ни к чему. Посмотрите какая она красивая, можно сказать, что сама запоминается.
*Если даны три стороны треугольника, то по данной формуле мы всегда можем вычислить его площадь.
Формула четвёртая
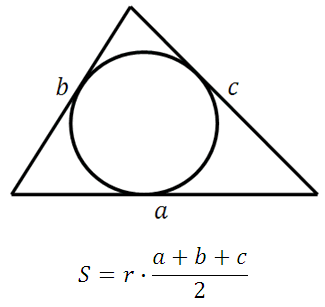
где r – радиус вписанной окружности
*Если известны три стороны треугольника и радиус вписанной в него окружности, то мы всегда можем найти площадь этого треугольника.
Формула пятая
где R – радиус описанной окружности.
*Если известны три стороны треугольника и радиус описанной около него окружности, то мы всегда можем найти площадь такого треугольника.
Возникает вопрос: если известны три стороны треугольника, то не проще ли его площадь найти по формуле Герона!
Да, бывает проще, но не всегда, иногда возникает сложность. Это связано с извлечением корня. Кроме того, данные формулы очень удобно применять в задачах, где дана площадь треугольника, его стороны и требуется найти радиус вписанной или описанной окружности. Такие задания имеются в составе ЕГЭ.
Давайте отдельно рассмотрим формулу:
Она является частным случаем формулы площади многоугольника, в который вписана окружность:
Рассмотрим её на примере пятиугольника:
Соединим центр окружности с вершинами данного пятиугольника и опустим из центра перпендикуляры к его сторонам. Получим пять треугольников, при чём опущенные перпендикуляры являются радиусами вписанной окружности:
Площадь пятиугольника равна:

Теперь понятно, что если речь идёт о треугольнике, то данная формула приобретает вид:
Формула шестая
Пусть сторона треугольника равна a, из противоположной вершины к этой стороне проведён произвольный отрезок образующий с ней угол (фи):

Тогда
Данная формула используется очень редко на практике, возможно вы её видите впервые, ну так просто написал, чтобы знали. Её ещё можно вывести преобразовав формулу площади четырёхугольника:
Также она является следствием из :
Что добавить? Есть ещё формулы треугольника связанные с координатами вершин, векторами на которых он построен. Об этом будет статья в будущем, не пропустите!
Площадь прямоугольного треугольника. Тут всё просто — она равна половине площади прямоугольника, то есть одной второй произведения катетов.
На этом всё! Успеха Вам!
Универсальные способы нахождения площади треугольника
В приведенных ниже формулах используются специальные обозначения. Мы расшифруем каждое из них:
- a, b, c – длины трех сторон рассматриваемой нами фигуры;
- r – радиус окружности, которая может быть вписана в наш треугольник;
- R – радиус той окружности, которая может быть описана вокруг него;
- α — величина угла, образованного сторонами b и с;
- β — величина угла между a и c;
- γ — величина угла, образованного сторонами а и b;
- h – высота нашего треугольника, опущенная из угла α на сторону а;
- p – половина суммы сторон a, b и с.
Логически понятно, почему можно находить площадь треугольника этим способом. Треугольник легко достраивается до параллелограмма, в котором одна сторона треугольника будет выполнять роль диагонали. Площадь параллелограмма находится умножением длины одной из его сторон на значение высоты, проведенной к ней. Диагональ разделяет этот условный параллелограмм на 2 одинаковых треугольника. Следовательно, совершенно очевидно, что площадь нашего исходного треугольника должна равняться половине площади этого вспомогательного параллелограмма.
S=½ a · b·sin γ
Согласно этой формуле, площадь треугольника находится умножением длин двух его сторон, то есть а и b, на синус образованного ими угла. Эта формула логически выводится из предыдущей. Если опустить высоту из угла β на сторону b, то, согласно свойствам прямоугольного треугольника, при умножении длины стороны a на синус угла γ получаем высоту треугольника, то есть h.
Площадь рассматриваемой фигуры находим путем умножения половины радиуса окружности, которую в него можно вписать, на его периметр. Иными словами, находим произведение полупериметра на радиус упомянутой окружности.
S= a · b · с/4R
Согласно данной формуле, необходимую нам величину можно найти путем деления произведения сторон фигуры на 4 радиуса окружности, вокруг нее описанной.
Эти формулы универсальны, так как дают возможность определить площадь любого треугольника (разностороннего, равнобедренного, равностороннего, прямоугольного). Можно это сделать и при помощи более сложных вычислений, на которых мы подробно останавливаться не станем.
Прямоугольный треугольник и его площадь.
Прямоугольный треугольник – это треугольник, у которого один угол равен 90 градусам (потому называется прямым). Прямой угол образуют две перпендикулярные линии (в случае с треугольником – два перпендикулярных отрезка). В прямоугольном треугольнике прямой угол может быть только один, т.к. сумма всех углов одного любого треугольника равна 180 градусам. Получается, что 2 других угла должны делить между собой оставшиеся 90 градусов, например 70 и 20, 45 и 45 и т.д. Итак, основное вы вспомнили, осталось узнать, как найти площадь прямоугольного треугольника. Представим, что перед нами вот такой прямоугольный треугольник, и нам необходимо найти его площадь S.
1. Самый простой способ определения площади прямоугольного треугольника высчитывается по следующей формуле:
В нашем случае, площадь прямоугольного треугольника равна: S = 2,5 см. * 3 см. / 2 = 3,75 кв.см.
В принципе, больше нет необходимости выверения площади треугольника иными способами, т.к. в быту пригодится и поможет только этот. Но существуют и варианты измерения площади треугольника через острые углы.
2. Для других способов вычисления необходимо иметь таблицу косинусов, синусов и тангенсов. Посудите сами, вот какие варианты вычисления площадей прямоугольного треугольника еще можно использовать:
Мы решили воспользоваться первой формулой и с небольшими помарками (чертили в блокноте и использовали старую линейку и транспортир), но у нас вышел верный расчет:
S = (2,5*2,5)/(2*0,9)=(3*3)/(2*1,2). У нас вышли такие результаты 3,6=3,7, но с учетом сдвига клеток, этот нюанс нам можно простить.
Задача. Найти площадь по двум сторонам и углу между ними
Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника
.
Решение
.
Для решения этой задачи используем формулу номер два из теоретической части урока.
Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ
Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60
В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов . Он будет равен корню из трех на два.
S = 15 √3 / 2
Ответ
: 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)
Как найти площадь треугольника через высоту и основание
Теорема 1
Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.
Математически это выглядит следующим образом
$S=\frac{1}{2}αh$
где $a$ — длина стороны, $h$ — высота, проведенная к ней.
Доказательство.
Рассмотрим треугольник $ABC$, в котором $AC=α$. К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.
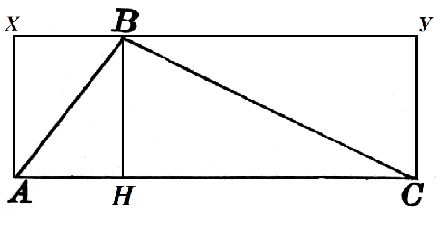
Площадь прямоугольника $AXBH$ равняется $h\cdot AH$, а прямоугольника $HBYC$ равняется $h\cdot HC$. Тогда
$S_ABH=\frac{1}{2}h\cdot AH$, $S_CBH=\frac{1}{2}h\cdot HC$
Следовательно, искомая площадь треугольника, по свойству 2, равняется
$S=S_ABH+S_CBH=\frac{1}{2}h\cdot AH+\frac{1}{2}h\cdot HC=\frac{1}{2}h\cdot (AH+HC)=\frac{1}{2}αh$
Теорема доказана.
Пример 2
Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице
Основание этого треугольника равняется $9$ (так как $9$ составляет $9$ клеток). Высота также равняется $9$. Тогда, по теореме 1, получим
$S=\frac{1}{2}\cdot 9\cdot 9=40,5$
Ответ: $40,5$.
Примеры решения задач
Задача 1
Периметр равностороннего треугольника составляет 36 см. Какова площадь данной геометрической фигуры?
Решение.
Первым действием будет нахождение длины стороны через известных периметр: 36:3=12 (см)
Второе действие основано на формуле: \(S=(a2√3)/4 = 144√3/4=36√3\)
Ответ: \(36√3\)
Задача 2
Площадь равностороннего треугольника равна \(25√3\). Какова длина его стороны?
Решение: Используя формулу площади равностороннего треугольника через известную длину стороны, получаем выражение:
\(S=(a2√3)/4\)
\(25√3=(a2√3)/4\)
\(25=a2\)
a=5
Ответ: сторона треугольника равна 5.
Задача 3
Площадь равностороннего треугольника равна \(49√3\). Чему равна высота этой фигуры?
Решение.
Первым действием находим длину его стороны:
\(S=(a2√3)/4\)
\(49√3=(a2√3)/4\)
\(49=a2\)
a=7
Во втором действии применяем формулу: \(h=a√3/2=7√3/2=3,5√3\)
Ответ: высота равна \(3,5√3\)
Задача 4
Радиус окружности, описанной вокруг равностороннего трегольника, равен 10. Найти площадь этого треугольника и длину его стороны.
Решение:
В первом действии применяем формулу:
\(S=3√3/4*R2\)
\(S=300√3/4=75√3\)
С другой стороны:
\(S=a2√3/4\)
\(75√3=a2√3/4\)
Сокращая √3, получаем: \(4a2=75\)
a=√18,75
Формулы, которыми можно воспользоваться в разных задачах
Известны длины сторон, и требуется найти площадь равнобедренного треугольника.
В этом случае нужно возвести в квадрат оба значения. То число, которое получилось от изменения боковой стороны, умножить на 4 и вычесть из него второе. Из полученной разности извлечь квадратный корень. Длину основания разделить на 4. Два числа перемножить. Если записать эти действия буквами, то получится такая формула:
Пусть она будет записана под №1.
Найти по значениям сторон площадь равнобедренного треугольника. Формула, которая кому-то может показаться проще, чем первая.
Первым действием нужно найти половину основания. Потом найти сумму и разность этого числа с боковой стороной. Два последних значения перемножить и извлечь квадратный корень. Последним действием умножить все на половину основания. Буквенное равенство будет выглядеть так:
Это формула №2.
Способ найти площадь равнобедренного треугольника, если известны основание и высота к нему.
Одна из самых коротких формул. В ней нужно перемножить обе данные величины и разделить их на 2. Вот как она будет записана:
Номер этой формулы — 3.
В задании известны стороны треугольника и значение угла, лежащего между основанием и боковой стороной.
Здесь, для того чтобы узнать, чему будет равна площадь равнобедренного треугольника, формула будет состоять из нескольких множителей. Первый из них — это значение синуса угла. Второй равен произведению боковой стороны на основание. Третий — дробь ½. Общая математическая запись:
Порядковый номер формулы — 4.
В задаче даны: боковая сторона равнобедренного треугольника и угол, лежащий между его боковыми сторонами.
Как и в предыдущем случае, площадь находится по трем множителям. Первый равен значению синуса угла, указанного в условии. Второй — это квадрат стороны. И последний также равен половине единицы. В итоге формула запишется так:
Ее номер — 5.
Формула, которая позволяет найти площадь равнобедренного треугольника, если известны его основание и угол, лежащий напротив него.
Сначала нужно вычислить тангенс половины известного угла. Полученное число умножить на 4. Возвести в квадрат длину боковой стороны, которое потом разделить на предыдущее значение. Таким образом, получится такая формула:
Номер последней формулы — 6.
Общие для всех треугольников формулы, в которых используются длины сторон или высот
Обозначения, принятые в них: стороны — а, в, с; высоты на соответствующие стороны н а, н в, н с.
1. Площадь треугольника вычисляется, как произведение ½, стороны и высоты, опущенной на нее. S = ½ * а * н а. Аналогично следует записать формулы для двух остальных сторон.
2. Формула Герона, в которой фигурирует полупериметр (его принято обозначать маленькой буквой р, в отличии от полного периметра). Полупериметр необходимо сосчитать так: сложить все стороны и разделить их на 2. Формула полупериметра: р = (а+в+с) / 2. Тогда равенство для площади фигуры выглядит так: S = √ (р * (р — а) * (р — в) * (р — с)).
3. Если не хочется использовать полупериметр, то пригодится такая формула, в которой присутствуют только длины сторон: S = ¼ * √ ((а + в + с) * (в + с — а) * (а + с — в) * (а + в — с)). Она несколько длиннее предыдущей, но выручит, если забылось, как находить полупериметр.
Формула Герона
Теорема 2
Если нам даны три стороны треугольника $α$, $β$ и $γ$, то его площадь можно найти следующим образом
$S=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
здесь $ρ$ означает полупериметр этого треугольника.
Доказательство.
Рассмотрим следующий рисунок:
По теореме Пифагора из треугольника $ABH$ получим
Из треугольника $CBH$, по теореме Пифагора, имеем
$h^2=α^2-(β-x)^2$
$h^2=α^2-β^2+2βx-x^2$
Из этих двух соотношений получаем равенство
$γ^2-x^2=α^2-β^2+2βx-x^2$
$x=\frac{γ^2-α^2+β^2}{2β}$
$h^2=γ^2-(\frac{γ^2-α^2+β^2}{2β})^2$
$h^2=\frac{(α^2-(γ-β)^2)((γ+β)^2-α^2)}{4β^2}$
$h^2=\frac{(α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α)}{4β^2}$
Так как $ρ=\frac{α+β+γ}{2}$, то $α+β+γ=2ρ$, значит
$h^2=\frac{2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α)}{4β^2}$
$h^2=\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2 }$
$h=\sqrt{\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2}}$
$h=\frac{2}{β}\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
По теореме 1, получим
$S=\frac{1}{2} βh=\frac{β}{2}\cdot \frac{2}{β} \sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$






























